边界层对流扩散方程在自适应网格上的高精度紧致格式
袁冬芳,曹富军,葛永斌
(1.内蒙古科技大学 理学院,内蒙古 包头 014010;2.宁夏大学 数学统计学院,宁夏 银川 750021)
0 引言
对流扩散方程广泛应用于许多实际物理问题的建模,如核废料污染、渗流驱动、海水入侵等,所以研究其精确、稳定和高效的数值方法具有十分重要的意义.当物理解足够光滑时一致网格上的高阶格式就可以得到满意的数值解,然而当物理解存在间断或大梯度时,采用均匀网格计算足够的精度就需要比较多的网格点,从而增加了存储空间、计算量和计算时间.合理的做法是在边界层和大梯度附近分布比较多的网格点,在物理解变化比较平缓的区域分布较少网格点.针对带边界层和大梯度问题的对流扩散方程高阶格式的研究已经引起了国内外研究者的广泛关注.文献[1-2]基于非均匀网格上函数的泰勒级数展开,结合残量修正法,推导了非均匀网格上对流扩散方程的高阶指数型紧致差分格式,结果表明该格式兼有高精度和高分辨率的优点,能够很好地适用于大梯度变化.文献[3]基于泰勒级数展开,构造了一种非均匀网格三点四阶精度的紧致差分格式,并对Burgers方程和对流方程进行求解.文献[4]基于泰勒级数展开法提出了求解一维定常对流扩散方程非均匀网格上的具有3~4阶精度的紧致差分格式.曹广满等[5]针对一维定常对流扩散方程提出了一种二阶非等距网格上的差分格式.献文[6-9]提出了非均匀网格上求解一维非定常对流扩散方程的紧致差分格式.文献[10-11]提出了求解二维定常对流扩散方程非均匀网格上的高精度紧致差分格式.然而,以上文献采用的非均匀网格均由网格分布函数来确定,且对于不同的算例需要指定不同的网格分布函数.同时需要不断调整网格伸缩系数从而对网格的疏密程度进行控制,网格分布函数及伸缩参数的选择直接影响数值计算的精度,很大程度上限制了该方法的适用性.
自适应网格算法根据实际问题需要在物理解变动较大的区域网格自动密集,而在物理解变化平缓区域网格相对稀疏,对于合理分布网格及高效和精确计算起着极其重要的作用[12-15].据我们所知,基于自适应网格的高阶紧致格式求解边界层对流扩散方程的研究鲜有报道.文中针对带边界层对流扩散问题提出自适应网格方法,根据物理解的特征对网格进行自适应加密,然后结合高精度紧致差分格式对一维边界层对流扩散方程进行求解.
1 高精度紧致格式
考虑定常对流扩散方程
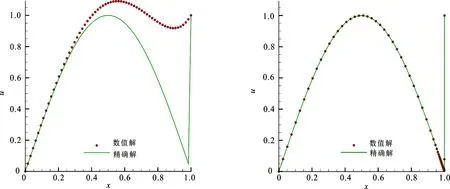
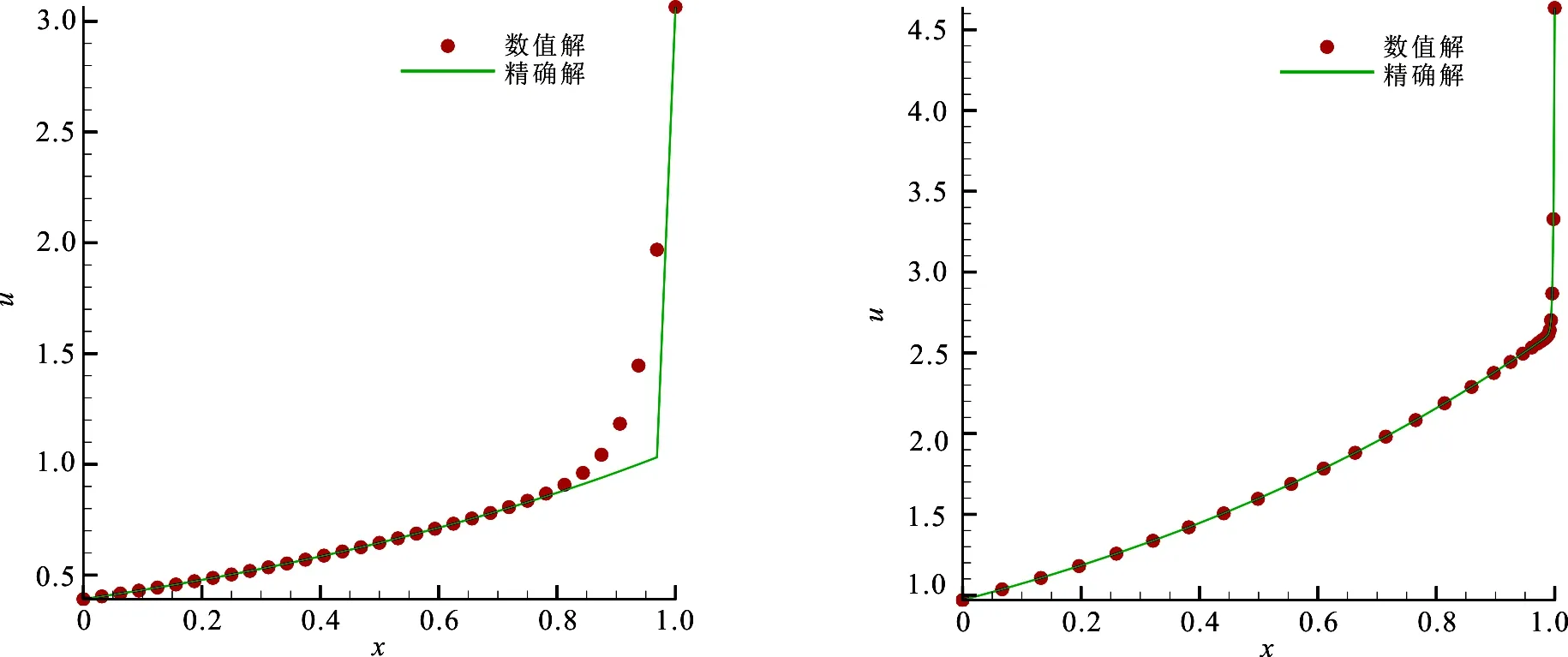
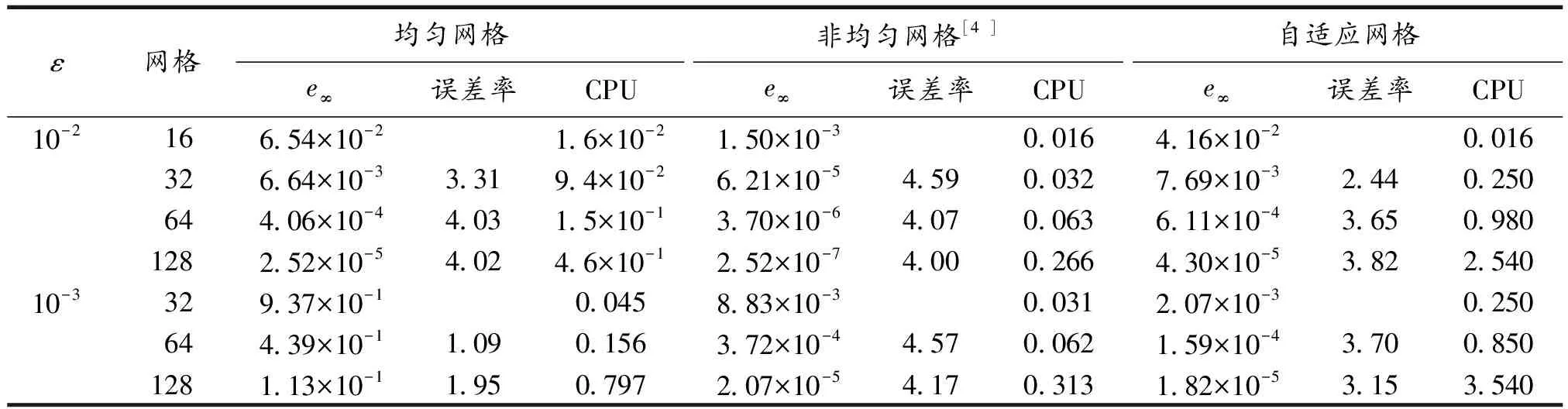
将区域[a,b]非均匀剖分为N个子区间:a≤x0 将(2)和(3)式相减,整理可得 将(2)和(3)式分别乘以xf和xb后相加,整理得 非均匀网格上的一阶和二阶导数的中心差分算子可表示为 将(6)和(7)式代入(1)式可得 (8) 其中,pi=p(xi),fi=f(xi),τi为截断误差,且 这里 为了得到高阶精度,对截断误差项(9)中的三阶和四阶导数项进行处理,并利用方程(1)可得 将(10)和(11)式代入(9)可得 将(12)式代入(8)式并整理可得非均匀网格上的高阶紧致差分格式 βui-1+αui+γui+1=Fi, (13) 其中 由泰勒级数展开与截断误差分析可知,格式(13)具有3~4阶精度.当xf≠xb时,格式(13)具有3阶精度;当xf=xb时退化为均匀网格,格式具有4阶精度. 类似地,在y方向定义hy=(d-c)/Ny,hfy=yj+1-yj=θfyhy,hby=yj-yj-1=θbyhy.同时令αy=θfyθby,βy=θfy+θby,γy=θfy-θby,则二维对流扩散方程在非均应网格上的紧致格式为[10-11]: (14) 其中Aij,Bij,Cij,Dij,Gij,Hij,Kij,Lij分别为 显见,格式(14)在非均匀网格(θx≠θy)上至少具有三阶精度,且网格为均匀网格(θx=θy=1)时退化为标准四阶紧致格式[10-11]. (ω-1ξx)x=0, 其等价于 (ωxξ)ξ=0, (15) (16)式将根据物理解的特点对网格进行自适应加密,迭代求解(16)式至收敛将得到新的网格分布. 以上网格自适应算法过程描述如下: 考虑矩形计算区域Ω=[a,b]×[c,d],将区域进行等距离散并将网格表示为{coord[0]},即 记均匀网格上的初始数值解为{u[0]}.令sgr(j)为第j行上每个区间上梯度的和,即 类似地,第i列上每个区间上梯度的和可表示为{sgc(i),i=0,1,…,Nx}.令jmax和imax分别表示为行和列上梯度变化最大的行和列号,即 记rmax和cmax分别表示jmax行和imax列上梯度最大的网格,即 记ylay=rmax/sgr(jmax),xlay=cmax/sgc(imax),ylay和xlay用于监测边界层的存在且根据值的不同,可以分为以下4种情形: 以情形 4为例,在x,y方向都存在边界层,则需要分别在x和y方向上交替实施一维网格自适应算法.记 当网格更新为{coord[1]}时,将初始值{u[0]}更新为{u(1)},即 重复以上过程,直到 ||coord[v+1]-coord[v]||<ε2, 则可以得到新的网格. 对于情形2和情形3可以采用类似的方式分别在x和y方向上实施一维自适应算法. 为了验证文中方法的精确性和可靠性,在定义域[0,1]内针对以下两个有精确解的对流扩散问题进行数值实验,并比较均匀网格和自适应网格上计算结果的精度和收敛阶. 算例1考虑线性常系数对流扩散问题 该问题的精确解为 该问题在x=1附近有一个边界层,因此采用如下变换函数生成非均匀网格: 其中,N是区域剖分后子区间的个数,λ是伸缩变化系数,用来调节网格点在某一区域的密集程度[4-8]. 图1给出了ε=10-4时均匀网格和自适应网格上的计算结果,看出均匀网格的计算结果在边界层附近产生很大的误差,自适应网格上的计算结果与精确解吻合得很好.表1给出了ε=10-2时均匀网格、非均匀网格和自适应网格上的最大误差和收敛阶.从表1可以看出,在相同网格数下非均匀网格和自适应网格上的误差明显比均匀网格上的误差小2个量级,如均匀网格上网格数N=128时的最大误差为1.984×10-4,然而自适应网格上网格数N=32时的误差即可达到相同的量级,因此自适应网格能够大大减少计算网格,充分说明了其优越性.从表1的收敛阶可见,自适应网格与非均匀网格上的收敛阶基本保持4阶精度,明显高于均匀网格上的精度. (a)均匀网格 (b)自适应网格 图1 均匀网格和自适应网格上的数值解(N=65,ε=10-4) Fig 1 The exact solution and numerical solutions under uniform mesh and adaptive mesh (N=65,ε=10-4) 表1 均匀网格与自适应网格上的最大误差与收敛阶,ε=10-2 算例2考虑二维对流扩散问题 该问题的精确解为 u(x,y)=ey-x+21/ε(1+y)1+1/ε. 图2给出了网格Nx=Ny=33,ε=10-3时精确解以及均应网格、非均匀网格和自适应网格上的数值解.图3比较了x=0,Nx=33,ε=10-3时均应网格和自适应网格上精确解和数值解的比较,从图中可见,自适应网格在边界层附近分布更多的网格点,且数值解与精确解一致. 图2 精确解以及不同网格上的数值解 图3 均匀网格与自适应网格上的精确解与数值解 表2比较了ε=10-2和ε=10-3时不同网格下的最大误差、CPU时间和收敛阶,其中非均匀网格的伸缩系数分别为λx=0.0,λy=0.55和λx=0.0,λy=0.9.从表2可见,当ε=10-2时,3种网格上的最大误差和收敛阶都接近于四阶精度;当ε=10-3时,均匀网格丧失了精度,非均匀和自适应网格依然能够得到比较合理的误差和收敛阶.需要指出的是,非均匀网格需要在已知边界层位置的情况下根据不同的网格和参数指定合理的网格伸缩系数,自适应网格在不知边界层位置的情况下可以根据初始值对网格进行迭代从而使其重新分布. 表2 不同网格上的最大误差、CPU时间及收敛阶 提出了二维计算区域上正交网格的自适应方法,并结合高精度紧致差分格对一维和二维对流扩散方程大梯度和边界层问题进行求解.该方法可以在现有代码中实现,也可以应用于边界层与坐标轴平行的问题.其根据初值采用迭代的方式进行网格自适应调整,有效改进了现有方法中事先指定边界层位置,并采用网格分布函数调整网格控制参数进行非均匀网格生成的缺点.数值算例表明:自适应网格方法能够合理地调节网格疏密,同时结合自适应网格方法与高阶格式对边界层问题进行求解可以提高数值解的精度,减少计算网格,降低计算量. 参考文献: [1] 田芳.一维对流扩散方程非均匀网格上的指数型高阶紧致差分格式[J].数学的实践与认识,2015(4):268. [2] 田芳,田振夫.非均匀网格上求解对流扩散问题的高阶紧致差分方法[J].宁夏大学学报(自然科学版),2009,30(3):209. [3] 孙建安,贾伟,吴广智.一种非均匀网格上的高精度紧致差分格式[J].西北师范大学学报(自然科学版),2014,51(4):31. [4] 薛文强,兰斌,葛永斌.一维定常对流扩散方程非均匀网格上的高阶紧致差分格式[J].西北师范大学学报(自然科学版),2013,50(4):16. [5] 曹广满,王彩华,齐海涛.对流扩散方程的非一致网格有限差分方法[J].天津师范大学学报(自然科学版),2010,30(1):7. [6] 黄雪芳,郭 锐,葛永斌.一维非定常对流扩散方程非均匀网格上的高精度紧致差分格 式[J].工程数学学报,2014(3):371. [7] 赵飞,陈建华,葛永斌.一维非定常对流扩散方程非均匀网格上的高阶紧致差分格式[J].西安理工大学学报,2013,29(4):475. [8] MOHEBBI A,DEHGHAN M.High-order compact solution of the one-dimensional heat and advection-diffusion equations[J].AppliedMathematicalModelling,2010,34(10):3071. [9] TIAN Z F,YU P X.A high-order exponential scheme for solving 1D unsteady convection-diffusion equations[J].JournalofComputationalandAppliedMathematics,2011,235(8):2477. [10] KALITA C,DASS A K,DALAL D C.A transformational-free HOC scheme for steady convection-diffusion on non-uniform grids[J].InternationalJournalforNumericalMethodsinFluids,2004,44(1):33. [11] GE Y B,CAO F J.Multigrid method based on the transformation-free HOC scheme on nonuniform grids for 2D convection diffusion problems[J].JournalofComputationalPhysics,2011,230(10):4051. [12] TANG H Z,TANG T.Adapative mesh methods for one-and two-dimensional hyperbolic conservation laws[J].SIAMNumericalAnalysis,2003,41(2):487. [13] YANG X,HUANG W,QIU J.A moving mesh WENO method for one-dimensional conservation laws[J].SIAMJournalofScientificComputing,2012,34:2317. [14] HU F X,WANG R,CHEN X.Y,et al.An adaptive mesh method for 1D hyperbolic conservation laws[J].AppliedNumericalMathematics,2015,91:11. [15] Van DAM A,ZEGELING P A.A robust moving mesh finite volume method applied to 1D hyperbolic conservation laws from magneto-hydrodynamics[J].JournalofComputationalPhysics,2006,216(2):526.2 自适应网格
2.1 一维问题
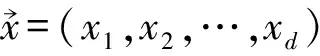
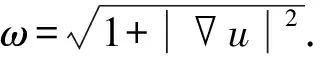
2.2 二维问题
3 数值算例

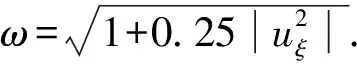

4 结束语

