Satellite proximate interception vector guidance based on differential games

Dong YE,Mingming SHI,Zhowei SUN

aResearch Center of Satellite Technology,Harbin Institute of Technology,Harbin Institute of Technology,Harbin 150001,China

bFaculty of Science and Engineering,University of Groningen,Groningen 9747AG,The Netherlands

1.Introduction

Satellites can be a tool to intercept the opponent’s critical satellite which serves in the space above the important field.In the satellite attacking-defense system,the attacking satellites often keep dormant on their hiding orbits.They will be revoked to perform orbital maneuvers and intercept the dangerous targets by the ground facilities or other early warning satellites.This interception problem is considered to enter the final phase when the attacking and escaping satellites move close enough so that the interceptor can identify the target with onboard electronic devices.

Massive papers have studied the control strategies for satellite interception when the target has no maneuverability.Based on the Clohessy-Wiltshire(CW)equation,Ichikawa and Ichimura1decomposed the satellite relative motion as the orbital planar motion and the motion outside orbital plane.The authors employed the fuel cost as the optimal objective and obtained a relative orbital control strategy,with three inplane and one out-plane impulsive maneuvers.It is easy to design or operate proximate orbit rendezvous or interception by impulsive method.However,the precision of impulsive guidance often cannot satisfy the mission requirement since it is an open-loop control method.As for continuous thrust interception,the miss distance of variable thrust control method can be reduced with various control strategies.Lu and Xu2studied the continuous satellite rendezvous problem for elliptical target’s orbits,in which the thrust magnitude is limited.In this paper,an adaptive control strategy is proposed to overcome the difficulty brought by non-communication between the rendezvous satellites.Based on the output feedback control,Singla et al.3designed a structured model reference adaptive controller to solve the automated orbital rendezvous problem with measurement uncertainties.In Ref.4,two Optimal Terminal Guidance(OTG)laws are developed for the exo-atmospheric interception with final velocity vector constraints.To make the problem solvable,a linear model is used to approximate the gravity difference between the target and the interceptor.The proposed guidance consumes much less fuel and requires a light computational load.Even the research results on non-maneuvering target interception or rendezvous have been applied in the real engineering,a more rigorous situation is that not only the interceptor can move toward the target,but the latter can perform orbital maneuver when it carries thrusters.Obviously,the interception will fail if the target can move in an impulsive way.Hence,continuous thrust is often presumed to make the problem sensible.

Traditionally,this problem is regarded as the noncooperative rendezvous.Two solving approaches have been proposed:(A)robust sliding mode controller;(B)robust H∞controller.For the former,the readers can refer to Ref.5,where Wu et al.developed a finite time observer and controller for the satellite interception with maneuverable target based on the non-singular terminal sliding mode theory.The method can make the position and velocity differences between the tracking and target satellites below an expected value.In Ref.6,the authors studied relative motion control of spacecraft rendezvous on low elliptical orbit.To cope with the J2perturbation,atmospheric drag and thrust failure,the authors developed two robust controllers based on the optimal sliding mode control and back stepping sliding control.For the latter,Gao et al.7developed a robust H1state feedback controller to solve the satellite rendezvous problem with parametric uncertainties,system disturbances and input constraints.Based on the Lyapunov analysis,a set of Linear Matrix Inequalities(LMIs)were obtained under multi-objective requirements.In Ref.8,Deng et al.studied the finite time satellite interception orbital control problem.A state feedback controller was designed by considering parametric uncertainties, finite time performance,control input constraints and pole assignment requirements.LMIs were used to solve the finite time controller.Simulations showed that the system was asymptotically stable and the requirements for system performance,input constraints and pole assignment were all satisfied.

Recently,another method is developed from the differential games theory which regards the interception problem where both sides have maneuvering capabilities as a pursuit-evasion game.Isaacs firstly concentrated on this problem and defined the two-side optimal solution as the saddle solution.9With quadratic objective functions,Menon and Calisa10,11obtained a feedback control strategy for spacecraft interception with saturated control input by the back stepping method.In Ref.12,a near-optimal feedback control for minimax-range pursuit-evasion problems between two constant-thrust spacecraft was generated by periodically solving the differential game problems with a modified first-order differential dynamic programming algorithm after the system state was updated.This new technique only requires a rough estimation of the optimal control to start the solving algorithm,instead of the accurate solution of a complete two-point boundary value problem,and hence can be implemented in the real time more easily.However,these papers assumed that the satellites have great maneuver capability,which is impossible in the real engineering.For nonlinear dynamics,the analytic solution for the two-person zero-sum differential games is often difficult to solve for the extremely complicated form of the Hamilton–Jacobi-Isaacs(HJI)partial differential equations.Hence,most literature dedicated to finding the open-loop saddle-point solution.Pontani and Conway13,14gave a numerical method to solve the open-loop trajectory of the three-dimensional satellite pursuit-evasion interception,where each spacecraft had a modest capability to maneuver.In the interception,the objective of the pursuer was to minimize the elapsed time after which it hit the target satellite,whereas the evader tried to postpone that instant as late as possible.A pre-solution of the saddle-point equilibrium was firstly derived by genetic algorithms.Then this solution was regarded as the initial guess and substituted into the semi-analytic method to find the accurate pursuit-evasion trajectory.The intensive random search and collocation method in Ref.13offers the possibility of searching a global optimal solution for the complex nonlinear pursuit-evasion games.However,it occupied high computational resources.In Ref.15,the authors applied sensitivity methods to the orbital pursuit-evasion problem in the same scenario as Ref.13,which sharply reduced the computation burden for the numerical solving of nonlinear satellite pursuit-evasion trajectories.This makes the real time satellite interception possible.

Compared with numerical solving open-loop trajectory,it is more difficult to derive the closed-loop control.Ghosh and Conway16presented an extremal- field approach to synthesize nearly-optimal feedback controllers for the non-linear twoplayer pursuit-evasion games.The proposed method utilized the universal Kriging technique to construct the surrogate model of the feedback controller,which was capable of generating the sub-optimal control based on current state information.In this method,the open-loop extremals were first generated of fline by a direct or indirect method,and then the real time feedback map was obtained by interpolating the controls of these open-loop extremals.With the same method,Stupik et al.17studied the satellite combat based on the linearized CW equation.The sub-optimal feedback solution was interpolated by the standard solutions which were pre-calculated with various initial conditions.Since the dynamics is reduced,the number of conjugates that needs to solve decreased from 12 in Ref.13to 3.This sharply improved the open-loop extremal’s of fline pre-solving ability.However,the method is derived for solving the open solution.Although the authors employed Kriging technique to construct a real-time feedback control,it still cannot guarantee the optimality of the solution and successful interception of agile satellite.Jagat and Sinclair18formulated the linear spacecraft pursuit-evasion interception as a two-player zero-sum differential game.A finite horizon linear control law was obtained by applying the Linear-Quadratic(LQ)differential game theory.Then a nonlinear control law was obtained by solving the state-dependent Riccati equation method.The results are not practical since in the real situation the evader will adopt the control which can make it escape away as soon as possible.Tartaglia and Innocenti19used the similar method to solve the in finite horizon rendezvous problem with two active spacecraft moving in the Local-Vertical Local-Horizontal(LVLH)rotating reference frame.However,this paper assumes that the satellites do not have thrust constraints and can perform large maneuvers.In a recent paper20,the authors developed a nonlinear vector guidance law for the exo-atmospheric interception with steering jets as the only possible method to move the vehicles.Capture time was analyzed for both idealand non-ideal interceptor,while time-to-go was given as the solution of a quartic polynomial equation.The proposed optimal guidance law could make the capture time to be optimal in both sides.The same method was applied to obtain a vector guidance law for the three-player con flict problem21in which the missile intended to intercept the target and also avoid the defender launched by the target,with bounded control for all players.The results in these two papers are more applicable to the exo-atomspheric interception of long-range missiles since they assume that the earth gravity difference between the pursuer and evader can be neglected compared with the control magnitude,which is invalid in the satellite application.Inspired by Refs.17,18,20,21,to design a more practical method for the satellite interception,this paper investigates the thrust constrained satellite pursuit-evasion games in the endgame.Same as Ref.17,the nonlinear dynamics is reduced to the linear CW equations.Then we introduce the zero miss variables and derive the optimal guidance law by the differential game theory.Time-to-go is estimated by solving a nonlinear integration equation.Several numerical examples are used to analyze the proposed satellite interception guidance law.

2.Relative orbital dynamics

The orbital dynamics are derived different from Refs.4,5in which the relative coordinate frame is established on the target satellite since they both assumed that the evading satellite has no or neglectable maneuvering ability.However,in this paper,the evading satellite is able to move away from the nominal orbit.It is difficult to derive a relative dynamic for the pursuer satellite if we continue to establish the relative coordinate frame on the target satellite since now its orbit is timevarying.To make the problem simple,we can establish the relative coordinate frame on a virtual satellite with time invariant orbit and derive both relative dynamics for the pursuer and evader on this virtual relative coordinate frame.The selection of the virtual satellite’s orbit can be arbitrary.However,considering the accuracy of the relative dynamics after choosing a specific virtual satellite orbit,the distance between the real satellite and the virtual one should be much small,compared with the distance between the virtual satellite and the Earth center.

As Fig.1 shows,we can establish a circular virtual satellite O which is close to the intercepting satellite.The relative orbital coordinate system is set up by setting the point O as the origin.The Ox axis directs along the temporal location vector rOof the virtual satellite.The Oz axis orientates to the direction of the orbital angular momentum.By rendering the Oxyz coordinate system to be right-handed,Oy axis lies in the virtual satellite’s orbital plane.

Fig.1 Virtual satellite and reference orbit.

We assume the following conditions to be satisfied:(A)The pursuit satellite moves as a point;(B)The virtual satellite has no maneuvering ability;(C)All the perturbations resulting from the earth non-spherical distribution,aerial force,solar radiation pressure and other celestial bodies’gravitational forces are neglected.The last two assumptions are necessary to make the shape of the reference virtual orbit invariant so that the relative orbital dynamics is tenable.

Let the position of the intercepting satellite in the earth inertial coordinate system be r.Then the dynamics of the pursuing and virtual satellites can be obtained as follows:

where rOand r are the magnitude of rOand r,respectively,μ is the earth gravitational constant,and u is the acceleration generated by the pursuing satellite’s control force.

Let the relative position of the pursuer in the virtual reference coordinate frame be

Then the relative orbital kinetic equation of the pursuit satellite can be given as

Since the virtual satellite reference orbital coordinate rotates as the satellite O moves,the motion equations of the pursuit satellite can be derived from the vector differentiation relations as follows:

where δr′and δr′represent the first-and second-order relative derivatives of δr,respectively,and ω stands for the angular velocity vector of relative coordinate frame established on the virtual satellite.

Combining the kinetic and motion equations,we get the pursuer’s dynamics:

The orbital angular velocity and acceleration are given as

Since the virtual orbit is circular,we have ω = μ/r3Oand ˙ω=0.If the distance between the pursuer and virtual satellite is far less than that from the pursuer to the earth center,namely ‖δr‖/r ≪ 1,we can simplify the pursuer’s dynamics Eq.(5)to the following:

where ux,uyand uzrepresent the three entries of the acceleration in the virtual orbital coordinate system.

The linear form of the dynamics above,well known as the CW equations,17makes the rendezvous or interception problem convenient to solve.De fining the system state variables to bewe can rewrite the dynamics in the state space form as

with

If the pursuer and evader are close in position,the virtual orbital reference coordinate system can be established by selecting a virtual satellite near these two satellites.The relative dynamics for both two players are developed as

where xPand xEare the states of the pursuer and evader in the virtual orbital coordinate system,respectively,and uPand uEare their accelerations.Note that,in this paper,we assume that each satellite carries a single thruster which can change its direction to control the satellite translational movement.Same as in Ref.17,we assume that the thrusts have constraints on their magnitudes

To make the interception achievable,we assume that the pursuer has a higher maneuver ability than the target,namely ρP＞ ρE.

We construct the new state by subtracting the relative state of the intercepting satellite with that of the target,xPE=xP-xE.Differentiating the new state,we can obtain

where C=-B.

3.Game formulation

The pursuer and evader compete for the final distance.With the dynamics Eq.(12)and the acceleration constraints Eq.(11),letwith rPEand vPEbeing the relative displacement and velocity between the pursuer and the evader respectively,and associate the terminal set as

where‖rPE‖ is the distance between the pursuer and the evader while riis the location vector for player i=P，E.In this scenario,the pursuer wants to apply the control uPso that the state will enter set T,while the evader tries to avoid it.

As in Ref.21,we construct the solution for this game in two steps.

Step 1.For a prescribed ending time tf,the terminal cost for the game dynamics is defined as

where D= ［I3，03］.For this pay-off function,we can find the optimal control pair ｛｝ satisfying the saddle point condition:

Step 2.For xPEand the required miss distance m and with the optimal control pair,we then change the final time tfuntil achieving the capture,namely the terminal costequals m.

Now we explicitly demonstrate these two steps.In order to simplify the analysis,we define the zero effort miss variables as

where Φ（tf，t）is the transition matrix of A.It satisfies

Let τ=tf-t,then the explicit form of Φ（tf，t）is given as the following by solving the matrix differential Eq.(17)

with

De fine the matrices BP（tf，t）and CE（tf，t）as

the game dynamics Eq.(12)and the terminal cost become

It is easy to know

We observe that the changing rate of the distance to the origin along a solution satisfies

where ξ=

Since the terms corresponding to these two players in dJ/dt are separable,the optimal control strategies for the pursuer and evader are obtained by minimizing or maximizing this rate

which gives the optimal controllers

We substitute them into the derivative Eq.(23)

where the fourth equality comes from Eq.(20)and the last from the fact that Φ12is also a function of τ.Here τ has the same meaning of time-to-go as in Ref.21To simplify the analysis,let θ = ωτ,and hence

Integrating it gives

with Δρ = ρP-ρE.

With this equation,we already find the optimal terminal cost for the game ending time tf=t+τ.Then we need to find a proper tf(in other words,proper θ)so that the capture condition is satisfied.Different with Refs.20,21,the Zero Effort Miss(ZEM)trajectory here depends not only on J but also on the final state of the ZEM variables.

4.Vector guidance based on time-to-go

Although the optimal control strategy has already been derived in Eq.(25),we still cannot give an explicit form since the time-to-go is unknown in this optimal control.Hence,the main problem for deriving a real-time guidance is to find the time-to-go.The corresponding unknown in our case is θgo.

Let m be the desired pursuer-evader satellite miss distance.We substitute it into Eq.(28)and get

Solving this equation,we can get the time required for the game to guarantee the miss distance.However,it is difficult to find an analytic solution since this equation is nonlinear,and more specifically,it contains an integration term which does not have an explicit primitive function.Hence we solve it by numerical method.First,we define

Taking its limit for θ → 0,we will have

We cannot ensure that f（θ）will be smaller than 0 since that it depends on the current state and the function f（θ）is nonlinear.This equation may have one solution,multiple solutions or no solution.Since our goal is to achieve the capture as soon as possible,we only care about the first zero point.

Investigation of different states shows that the shape of f（θ）has the following four types:

Case 1.df（θ）/dθ ＜ 0 for θ in a sufficient long interval.As θ increases,f（θ）will decrease and finally have a zero point.This is shown in Fig.2(a).

Case 2.df（θ）/dθ ＞ 0 when θ is small,and then it decreases as θ increases.It will decrease below zero in a sufficient long interval.Hence f（θ） first increases and then decreases later.Finally,f（θ）decreases below zero for the negative value of df（θ）/dθ.For this case,Fig.2(b)illustrates the shape of f（θ）.

Case 3.df（θ）/dθ ＜ 0 when θ is small but it increases as θ increases,and after certain time it becomes greater than zero.Hence f（θ）decreases at first,being negative at certain point,and then it increases and becomes positive later.The curve of f（θ）for this case is shown in Fig.2(c).

Case 4.df（θ）/dθ ＜ 0 at the beginning,and then it climbs up to be larger than zero,with a positive local minimum.As θ increases,df（θ）/dθ is negative finally,so f（θ）is initially positive and becomes negative after one fluctuation.See Fig.2(d)for this case.

With the aforementioned analysis for the shape of f（θ）,we propose a numerical algorithm to find the time-to-go.Given the current state xPE,we first calculate the initial value of the derivative of f（θ）.

(1) （df（θ）/dθ）|θ=0＞ 0，and then we know that the curve of f（θ）is like Fig.2(b).In order to solve Eq.(30),we first find a point θ0which makes f（θ）negative.This can be done by selecting a small point and increasing this value exponentially until f（θ）＜ 0 is satisfied.After searching θ0,θgocan be solved numerically by the Newton–Raphson method

θgocan be obtained by iterating this process until the convergence accuracy being satisfied.The convergence order for Newton method is 2,which makes the algorithm converge fast to the solution.However,now we still do not know the derivative of f（θ）.To give an explicit form of f′（θi）,we differentiate f（θ）and get

Since y（θ）=DΦ（θ/ω）xPE,we know

Substituting it into Eq.(33),we have

(2)If （df（θ）/dθ）θ=0＜ 0,then it may have an increasing trend which leads to a zero point(see Fig.2(c)),may increase later but finally decrease to be negative(see Fig.2(d)),or may be negative for all θ ＞ 0(see Fig.2(a)).

For the first two situations,we search a point^θ0such thatis positive.Then the solution for df（θ）/dθ=0 is calculated by numerical methods.In this paper,we use the simple bisection method with^θ0being the starting point.We can still use Newton solving method here,but the simple bisection method is more robust to the unknown shape of df（θ）/dθ.

We then set θ0as the solution for df（θ）/dθ=0 and compute the value of f（θ0）.From Fig.2(c)and Fig.2(d),we know that f（θ0）may be positive or negative.If f（θ0）＜ 0,we can repeatedly apply Newton gradient method to the equation f（θ）=0 and obtain the solution θgo.If f（θ0）is positive as in Fig.2(d),we can first find the point θ0which makes f（θ）＜ 0 by the same method in situation(1)and then give θgoby the simple bisection method.

For the last case,it is not possible to find an initial point θgoat which df（θ）/dθ is positive as above.However,we can still find the time-to-go with the same method as that in situation(1).

After solving the time-to-go,we then put it into the matrix Φ（θ）and obtain the nonlinear vector guidance strategy Eq.(23).From Eq.(29),we know if the intercepting satellite applies the optimal control,then the norm of ZEM trajectory‖y（θ）‖ is always lower bounded by

Fig.2 Curve of f（θ）in four cases.

Since Bl（θ）is positive,we have the following remarks

Remark 1.For the general pursuit-evasion games,in Ref.2,the authors showed there may exist a singular area,in which the optimal ZEM trajectory can be negative during some time interval while the optimal control strategy is arbitrary.However,there is no such singular area in our case.

Remark 2.Since ‖y（θ）‖ is lower bounded by Bl（θ）while Bl（θ）

is the denominator of the guidance law,we know that the optimal guidance law never chatters.

Remark 3.Usually,ZEM is the miss distance at the final time of the game if both players do not apply any control.However,in this paper the norm of ZEM is the game miss distance if both players play optimally.In the real situation,if both sides adopt the optimal control,it is easy to know that the game’s trajectory will be the same as the optimal trajectory.Hence the ending time of the game will be the same as tf.

Remark 4.The ending time of the game depends on the players’control strategies.For the interceptor,if the opponent uses other non-optimal control,the game trajectory will be different from the optimal one.Then the ending time needs to compute based on the current state after each sampling.

Remark 5.If both the pursuer and evader play optimally,we know that the ending time of the interception t*fhas a meaning of saddle solution,namely

This implies that if the evading satellite does not apply an optimal control strategy,the ending time of the game will be less thanHence we actually give a solution for the problem in Ref.17where the authors want to find an optimal control so that the intercepting time is minimal in the event that the target uses its own optimal control to maximize this time.

Remark 6.Following Remark 5,we know that the calculated time-to-go at the current instant should be smaller than that for the instant before the current time,namely θgo（t2）≤ θgo（t1）

for t1≤ t2.Hence the estimation of θ0for t2instant can be replaced by θgo（t1）.This would improve the accuracy and speed of the proposed algorithm.

5.Numerical example

In this section,we present the numerical simulation and discussion for the proposed vector guidance law.We assume that the target satellite moves in a circular orbit of radius rE=6878.165 km while the intercepting satellite is adjacent to the target.The mass of the target is 500 kg.It has a single thrusterwhich can exertthe force maximally up to TE=50 N,while the intercepting satellite is smaller with mass 100 kg and carries a thruster with maximum force TP=20 N.Hence, we know the orbit angular velocity ω=1.24×10-3rad/s and the acceleration bounds ρP=0.2 m/s2,ρE=0.1 m/s2.We choose the virtual orbit as the target satellite’s original orbit,and let the virtual satellite O be the same as the target before the pursuit-evasion game and move along the virtual orbit after the game starting.We assume that the initial states of the pursuer and evader are

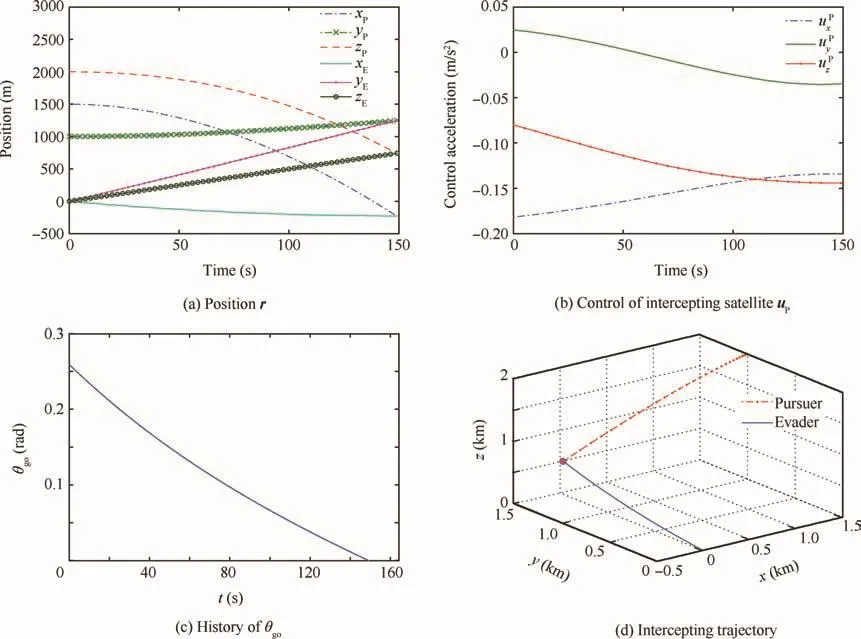
Fig.3 Interception when uE=0.

Fig.4 Interception when uEis optimal.

For all the examples,we assume that the miss distance m=0.1 m and the satellites take sampling every 0.1 s.

We first assume that the target does not discover the intercepting satellite,and hence it will not apply any control to escape from the pursuer.Fig.3 shows the simulation results for this case.

Fig.3(a)illustrates the positions of the pursuer and evader,from which we can find the corresponding position components approach the same points.Finally,the intercepting satellite collides with the target.Fig.3(b)shows that the control of the pursuer does not chatter,where uPx,uPyand uPzdenote the elements of the pursuer’s control acceleration in three dimensions.Fig.3(c)shows the history of θgocomputed by the intercepting satellite after each sampling.We can find that this curve is nonlinear,and this is because the evader does not use the optimal control during the interception.Fig.3(d)gives the intercepting trajectory.Simulation shows that the intercepting satellite completes the mission after 149.2 s.

Then we consider the situation that the evader also uses the optimal guidance strategy.The initial state for this case is the same as that in the previous example.Simulation results are illustrated in Fig.4.

Fig.5 Interception when uEis not optimal.

The pursuit-evasion game ends after 208.7 s.It is longer than the previous example since now the target also uses its optimal control which postpones the mission completing time.Fig.4(c)illustrates the three elements of the evader’s control acceleration.From Fig.4(b)and Fig.4(c),we can find that if both players apply the optimal control,the real control trajectories are near-linear before the end of the game,while at the time around the ending of the game,the controls fluctuate slightly.This is because we cannot give an analytic expression to compute θgoand the numerical method really depends on the iteration accuracy.This makes the real applied control slightly deviate from the optimal strategy.From Fig.4(d),we can find that θgodecreases linearly,which conforms to Remark 3 that when both players apply the optimal control strategies,the final game time is constant and θgodecreases linearly as the real time increases.

In the last example,the evader applies the following control:

which is not optimal.The simulation results are shown in Fig.5.In this case,the interception ends after 149.0 s,less than that of the second case.From Fig.5(b),we can find that when the game nearly ends,the control of the pursuer is gradually similar as that of the evader.This observation may be extended to the general case.From Fig.5(c),we know that the estimated time-to-go is not linearly decreasing since the evader does not apply the optimal guidance law.

6.Conclusions

This paper investigates the proximate satellite interception problem.Reduced linear dynamics is established by choosing a virtual circular reference orbit.Then game theory is applied to derive the optimal vector guidance law with miss distance as the payoff function.A numerical method to solve the time-togo from the highly complex ZEM trajectory equations is proposed based on the Newton-gradient method.

The vector guidance proposed in the present paper can guarantee that the miss distance of the satellite interception satisfies the mission requirement.If both sides apply the optimal control strategies,the time-to-go decreases linearly as time increases and the game ending time is a saddle point which means that if the pursuer applies other control strategies,target capturing will be prolonged while if the evader applies nonoptimal control the game ending time will decrease.This actually solves the pursuit-evasion game problem with interception time as the payoff function.Later work will consider the measurement noises,different sampling rate,sampling delay and hybrid dynamics.

Acknowledgements

This work was co-supported by the National Natural Science Foundation of China (Nos.61603115,91438202 and 91638301),China Postdoctoral Science Foundation(No.2015M81455),the Open Fund of National Defense Key Discipline Laboratory of Micro-Spacecraft Technology of China(No.HIT.KLOF.MST.201601),and the Heilongjiang Postdoctoral Fund of China(No.LBH-Z15085).

1.Ichikawa A,Ichimura Y.Optimal impulsive relative orbit transfer along a circular orbit.J Guid Control Dyn 2008;31(4):1014–27.

2.Lu S,Xu S.Adaptive control for autonomous rendezvous of spacecraft on elliptical orbit.Acta Mech Sin 2009;25(4):539–45.

3.Singla P,Subbarao K,Junkins JL.Adaptive output feedback control for spacecraft rendezvous and docking under measurement uncertainty.J Guid Control Dyn 2006;29(4):892–902.

4.Yu W,Chen W,Yang L,Liu X,Zhou H.Optimal terminal guidance for exoatmospheric interception.Chin J Aeronaut 2016;29(4):1052–64.

5.Wu SN,Wu GQ,Sun ZW.Spacecraft relative orbit finite-time control for proximity to non-cooperative strategy.J Dalian Univ Technol 2013;53(6):885–92[Chinese].

6.Imani A,Beigzadeh B.Robust control of spacecraft rendezvous on elliptical orbits:optimal sliding mode and back stepping sliding mode approaches.Proc Inst Mech Eng G J Aerosp Eng 2016;230(10):1975–89.

7.Gao H,Yang X,Shi P.Multi-objective robust H∞control of spacecraft rendezvous.IEEE Trans Control Syst Technol 2009;17(4):794–802.

8.Deng H,Sun Z,Zhong W,Chen C.Finite time optimal control for non-cooperative targets rendezvous with multi-constraints.J Harbin Inst Technol 2012;44(11):20–6[Chinese].

9.Isaacs R.Differential games:a mathematical theory with applications to warfare and pursuit,control and optimization.New York:Courier Corporation;1999.p.200–31.

10.Menon PKA,Calise AJ.Interception,evasion,rendezvous and velocity-to-be-gained guidance for spacecraft.AIAA guidance,navigation and control conference;1987 Aug 17–19,Monterey,USA.Reston:AIAA;1987.p.334–41.

11.Menon PKA,Calise AJ.Guidence laws for spacecraft pursuit evasion and rendezvous.AIAA guidance,navigation,and control conference;1988 Aug 15–17;Minneapolis,USA.Reston:AIAA;1988.p.688–97.

12.Anderson GM.Feedback control for a pursuing spacecraft using differential dynamic programming.AIAA J 1971;15(8):1084–8.

13.Conway BA,Pontani M.Numerical solution of the three dimensional orbital pursuit-evasion game.J Guid Control Dynam 2009;32(2):474–87.

14.Pontani M.Numerical solution of orbital combat games involving missiles and spacecraft.Dyn Games Appl 2011;1(4):534–57.

15.Hafer W,Reed H,Turner J,Pham K.Sensitivity methods applied to orbital pursuit evasion.J Guid Control Dyn 2015;38(6):1118–26.

16.Ghosh P,Conway B.Near-optimal feedback strategies for optimal control and pursuit-evasion games:a spatial statistical approach.AIAA/AAS astrodynamics specialist conference;2012 Aug 13–16;Minneapolis,USA.Reston:AIAA;2012.p.1–15.

17.Stupik J,Pontani M,Conway B.Optimal pursuit evasion spacecraft trajectories in the hill reference frame.AIAA/AAS astrodynamics specialist conference;2012 Aug 13–16,Minneapolis,USA.Reston:AIAA;2012.p.1–15.

18.Jagat A,Sinclair AJ.Optimization of spacecraft pursuit-evasion game trajectories in the euler-hill reference frame.AIAA/AAS astrodynamics specialist conference;2014 Aug 4–7,San Diego,USA.Reston:AIAA;2014.p.1–20.

19.Tartaglia V,Innocenti M.Game theoretic strategies for spacecraft rendezvous and motion synchronization.AIAA guidance,navigation,and control conference;2016 Jan 4–8;San Diego,USA.Reston:AIAA;2016.p.1–13.

20.Gutman S,Rubinsky S.Exoatmospheric thrust vector interception via time-to-go analysis.J Guid Control Dynam 2016;39(1):86–97.

21.Rubinsky S,Gutman S.Vector guidance approach to three-player con flict in exo-atmospheric interception.J Guid Control Dynam 2015;38(12):2270–86.