一类循环MDS矩阵的构造及计数

董新锋 董新科 李 枫

(1.保密通信重点实验室 四川成都 610041； 2.西南科技大学计算机科学与技术学院 四川绵阳 621010)

扩散部件的设计是密码算法设计的重要组成部分，目前的扩散部件主要有MDS矩阵、基于循环移位和异或运算的线性变换、比特置换、二元矩阵等。扩散部件设计的好坏直接影响着密码算法的安全性和效率[1-3]，采用差分分支数和线性分支数较大的扩散结构可以使密码算法更好地抵抗差分攻击和线性攻击，采用结构简单的扩散部件，有利于密码算法的快速实现。

MDS(最大距离可分码)矩阵的差分分支数和线性分支数相等，且达到最大[4]，故利用MDS矩阵设计分组密码的扩散结构是一种常用的方法。目前，MDS矩阵作为扩散部件被广泛应用于密码算法的设计中，如AES算法、CLEFIA算法、SMS4算法等都采用MDS矩阵，设计扩散结构。此外，为了保证密码算法的快速有效实现，MDS矩阵应具有较少的元素且元素的数值较小，例如AES算法中使用的MDS矩阵为循环移位矩阵，且只含有GF(28)上的3个不同的数值{1,2,3}，CLEFIA算法中使用的MDS矩阵为Hadamard矩阵，只含有GF(28)上的4个不同的数值{1,2,4,6}和{1,2,8,10}。

如何构造能够快速实现的MDS矩阵一直是人们关心的重要问题。文献[5]提出可以分别从循环移位矩阵、Cauchy矩阵以及Hadamard矩阵等特殊的矩阵中搜索出便于实现的MDS矩阵。文献[6]与文献[7]提出了利用Cauchy型矩阵设计MDS矩阵的思想和构造方法，但能构造出的MDS矩阵的个数不多，即当矩阵的级数给定时，这两种方法都只能构造出一个或少数几个MDS矩阵。文献[8]基于Cauchy矩阵以及Hadamard矩阵的构造方法给出了一类Cauchy-Hadamard矩阵的构造方法。文献[9-14]研究了通常情形下MDS矩阵的构造方法。文献[15-19]研究了轻量级MDS变换的构造方法。

本文将在Cauchy矩阵构造方法的基础上，提出一种循环移位MDS矩阵，并给出了这类矩阵的结构、构造方法和个数，是循环移位MDS矩阵的一种新的构造方法。由于这类MDS矩阵的结构非常简明，且构造方法简单，包含较少的不同元素，因而能够快速有效实现。

1 准备知识

本文用⨁表示逐位模2加，用+表示实数加或实数模2m加，用a-1表示有限域GF(2n)中元素a的乘法逆元。

对于y=(y1,y2,…,ym)∈GF(2n)m，本文均用W(y)表示y=(y1,y2,…,ym)中非0元的个数。

对于GF(wn)上m×m矩阵A定义的线性变换f(x)=Ax，其差分分支数达到最大值m+1等价于其线性分支数达到最大值m+1。当其差分分支数达到最大值时，则称A为MDS矩阵。

下面首先介绍线性变换的差分分支数Bd和线性分支数Bl的定义。

定义1 设f(x)=Ax且A是GF(2n)上的m×m矩阵，则

Bd=min{W(α)+W(Aα)|α∈GF(2n)m{0}}

Bl=min{W(ATα)+W(α)|α∈GF(2n)m{0}}

其中矩阵AT为矩阵A的转置矩阵。此处用+表示实数加。

本文以下部分均使用+表示实数模2m加。

定义2 设A=(aij)2m×2m是GF(2n)上的2m×2m矩阵，如果当0≤i,j≤2m-1时，均有aij=a0(i+j)，则称A为有限域上的一个循环(Cyclic)移位矩阵，并简记为A=Cyc(a00,a01,…,a0(2m-1)).

定义3[6]设x0,x1,…,xm-1,y0,y1,…,ym-1是GF(2n)中的互异元，对0≤i,j≤m-1，令aij=(xi,yj)-1，则称矩阵(aij)m×m为有限域GF(2n)上由X={x0,x1,…,xm-1}和Y={y0,y1,…,ym-1}生成的Cauchy矩阵。

文献[6]证明了有限域GF(2n)上的Cauchy矩阵都是MDS矩阵，因而也称Cauchy矩阵为Cauchy型MDS矩阵。

下面给出Cauchy-Cyclic型MDS矩阵的定义。

定义4 如果有限域GF(2n)上的2m×2m矩阵同时是Cyclic矩阵和Cauchy矩阵，则称该矩阵为Cauchy-Cyclic型MDS矩阵，简称为C-C矩阵。

2 C-C型MDS矩阵的构造及计数

定理1 设x0,x1,…,x2m-1∈GF(2n)且互不相同，则存在Y∈GF(2n)m，使得由X={x0,x1,…,x2m-1}和Y能够决定一个C-C矩阵的充要条件是xi⨁xj=x0⨁xi+j对0≤i,j<2m都成立，且存在GF(2n)中的非零元δ，使得xi⨁x0≠δ对0≤i<2m都成立。

证明：

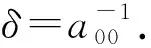
由A是C-C矩阵知a00=aii=(xi⨁yi)-1，从而

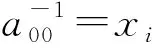
由y0≠xi和y0=x0⨁δ知xi⨁x0≠δ，

再由aij=a0(i+j)以及aij=(xi⨁yj)-1和a0(i+j)=(x0⨁y(i+j))-1知xi⨁yj=x0⨁yi,j，从而有xi⨁x0=yj⨁yi+j=(xi,j⨁δ)⨁(xj⨁δ)=xi,j⨁xj.

这说明必要性成立。

设i≠j，则xi⨁xj=x0⨁xi,j≠0，故x0,x1,…,x2m-1是GF(2n)上互不相同的元素。

令yi=xi⨁δ，则y0,y1,…,y2m-1也是GF(2n)上互不相同的元素。

由于xi⨁yj=xi⨁xj⨁δ=xi(j⨁x0⨁δ≠0，故x0,x1,…,x2m-1,y0,y1,…,y2m-1互不相同，因为由X和(0,y1,…,y2m-1)能够生成一个Cauchy矩阵(aij)2m×2m，其中aij=(xi⨁yi)-1.

再由aii=(xi⨁yi)-1=(xi⨁xj⨁δ)-1=(xi+j⨁x0⨁δ)-1=(yi+j⨁x0)-1=a0(i+j)，即知(aij)2m×2m是循环矩阵，因而是C-C矩阵。

这说明充分性成立。

定理1解决了利用有限域GF(2n)中2m个不同元{x0,x1,…,x2m-1}通过构造C-C矩阵的方法构造MDS矩阵时{x0,x1,…,x2m-1}应当满足的条件，其证明过程给出了C-C矩阵的构造结构。

定理1说明构造C-C矩阵等价于构造GF(2n)中满足xi⨁xj=x0⨁xi+j不同元{x0,x1,…,x2m-1}，并从GF(2n){0,x1⨁x0,x2⨁x0,…,x2m-1}中选取一个元作为δ，因此，也称C-C矩阵为基于{δ,x0,x1,…,x2m-1}构造的C-C矩阵。

下面解决C-C矩阵的计数问题。

定理2 设A=(aij)2m×2m和B=(bij)2m×2m是GF(2n)上基于{δ,x0,x1,…,x2m-1}和{δ",y0,y1,…,y2m-1}构造的C-C矩阵，则A=B的充要条件是δ=δ"且存在ε∈GF(2n)，使得当0≤i≤2m-1时都有xi⨁yi=ε.

证明：

由aij=(xi⨁xj⨁δ)-1=[(yi⨁ε)⨁(yj⨁ε)⨁δn]-1=(yi⨁yj⨁δ")-1=bij,易知充分性成立。

由aij=(x0⨁xi,j⨁δ)-1知a00=δ-1，

同理知b00=δ"-1，

故由A=B可知δ=δ".

设x0⨁y0=ε，则由(x0⨁xi⨁δ)-1=ai0=bi0=(y0⨁yi⨁δ")-1可知xi⨁yi=ε.

即必要性成立。

定理2说明，基于{δ,x0,x1,…,x2m-1}构造的C-C矩阵与基于{δ,0,x1⨁x0,x2⨁x0,…,x2m-1}构造的C-C矩阵相等，因而只需基于{δ,0,x1⨁x0,x2⨁x0,…,x2m-1⨁x0}构造C-C矩阵即可。

下面考虑基于{δ,0,x1⨁x0,x2⨁x0,…,x2m-1⨁x0}构造的C-C矩阵的计数情形。

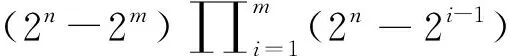
证明：

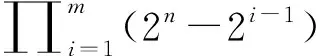
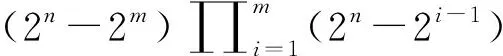
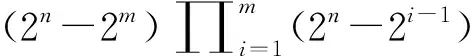
3 构造方法及实例

由上节的相关结果可知，C-C矩阵的构造可以采用下述的步骤完成。

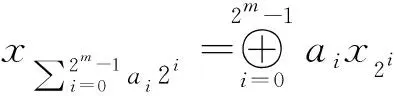
Step 4 对0≤i,j<2m-1，令aij=(xi+j⨁δ)-1,则矩阵A=(aij)2m×2m是GF(2n)上的一个2m阶的C-C矩阵。

下面给出构造GF(28)上的一个4阶MDS矩阵的实例。

选取的8次不可约多项式：f(x)=x8+x4+x3+x2+1。

选取{δ,x0,x1,x2,x3}={δ,0,1,x,x+1}，其中x为GF(28)上的本原元，δ=x2。

根据aij=(xi+j⨁δ)-1得到的4阶MDS矩阵(0x表示16进制前缀)：

测试结果表明，上述的4阶矩阵具有最大的分支数5，是循环MDS矩阵。

4 结束语

本文研究了Cauchy矩阵的构造方法，在此基础上构造了一类循环移位MDS矩阵(C-C矩阵)，并解决了C-C矩阵的构造方法和计数问题。

本文的研究结果为循环移位MDS矩阵的构造方法提供了一种新的途径，丰富了密码算法扩散部件的选择，对密码算法的设计具有实际的应用价值。

如何快速构造元素数值较小的循环移位矩阵或Hadamard矩阵是进一步需要解决的问题。

[1] SCHNEIER B,KELSEY J, WHITING D,et al.Twofish:A 128-bit block cipher[OL].Available at http://www.schneier.com/,2007-2-2.

[2] WANG M Q.Differential cryptanalysis of present[OL]. http://eprint.iacr.org/2007/408.

[3] WU W L,ZHANG W T, FENG D G.Impossible differential cryptanalysis of reduce round ARIA and camellia[J].Journal of Computer Science and Technology,2007,22(3):449-456.

[4] KANG J S,HONG S, LEE S J,et al.Practical and provable security against differential and linear cryptanalysis for substitution-permutation networks[J].ETRI Journal,2001,23(4):158-167.

[5] XIAO L, HEYS H.Hardware design and analysis of block cipher omponents[C].Proceedings of the 5th International Conference on Information Security and Cryptology-ICISC’02,2003 LNCS 2587:164-181.

[6] YOUSSEF A,MISTER S, TAVARES S.On the design of linear transformations for substitution permutation encryption networks[C].Workshop on Selected Areas in Cryptography-SAC’97,Ottawa,Workshop record,1997:40-48.

[7] BLOMER J,KALFANE M, KARPINSKI M,et al.An xor-based erasure-resilient coding scheme[R/OL].Technical Report TR-95-048.International Computer Science Institute,August 1995.ftp://ftp.icsi.berkeley.edu/pub/techreports/1995/tr-95-048.ps.gz.

[8] 崔霆，金晨辉.对合Cauchy-Hadamard型MDS矩阵的构造[J].电子与信息学报，2010, 32(2): 500-503.

[9] MALIK M Y, NO J S. Dynamic MDS Matrices for Substantial Cryptographic Strength[OL]. http://eprint.iacr.org/2011/177.

[10] GUPTA K C, RAY I G. On constructions of MDS matrices from companion matrices for lightweight cryptography[OL]. http://eprint.iacr.org/2013/056.

[11] DEHNAVI S M, MAHMOODI A, MIRZAEE M R, et al. Construction of new families of MDS diffusion layers[OL]. http://eprint.iacr.org/2014/011.

[12] KOLAY S, MUKHOPADHYAY D. Lightweight diffusion layer from thekthroot of the MDS matrix[OL]. http://eprint.iacr.org/2014/498.

[13] SIM S M, KHOO K, OGGIER F, et al. Lightweight MDS inrolution matrices[M]//Fast Software Encryption. Springer Berlin Heidelberg.2015:471-493.

[14] ZHAO R, ZHANG R, LI Y Q, et al. On constructions of a sort of MDS block diffusion matrices for block ciphers and hash functions[OL]. http://eprint.iacr.org/2015/449.

[15] SUMANTA S, SIANG M S. A deeper understanding of the XOR count distribution in the context of lightweight cryptography[OL]. http://eprint.iacr.org/2016/422.

[16] SUMANTA S, HABEEB S. Lightweight diffusion layer importance of toeplitz matrices[OL]. http://eprint.iacr.org/2016/835.

[17] SUMANTA S, HABEEB S. Analysis of toeplitz MDS matrices[OL]. http://eprint.iacr.org/2017/368.

[18] SUMANTA S, HABEEB S, RAJAT S, et al. Lightweight design choices for LED-like block ciphers[OL]. http://eprint.iacr.org/2017/1031.

[19] SUMANTA S, HABEEB S. Bounds on the differential branch number of permutations[OL]. http://eprint.iacr.org/2017/990.