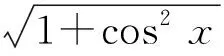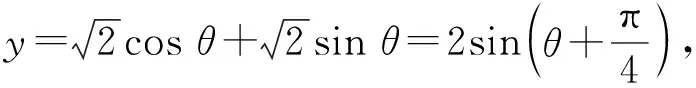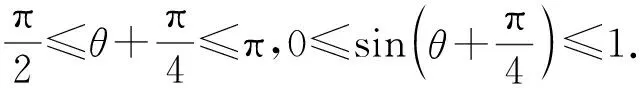构造:让解题突破思维瓶颈①
段志贵
(盐城师范学院数学与统计学院 224002)
构造方法作为一种数学方法,能够具体反映出在数学发现过程中所表现出来的创造性思维[1].构造法解题的实质是根据数学问题的条件或结论的特征,用条件中的元素为“原件”,用已知数学关系为“支架”,构造出一种相关的数学对象、一种新的数学形式,从而使问题转化并得到解决[2].
不同于一般的逻辑方法,构造法属于非常规思维.这一思维体现在当某些数学问题在使用通常办法,按定势思维去解决很难奏效时,依据问题的相关特征或性质,从新的角度,用新的观点观察、分析、解释对象,抓住反映问题条件与结论之间的内在联系,把握问题的背景、结构等关系上的特点,构造出满足条件或结论的新的数学对象,或构造出一种新的问题形式.通过构造,使得原问题中隐晦不清的关系和性质在新构造的数学对象(或问题形式)中清楚地表现出来,从而突破思维瓶颈,借助该数学对象(或问题形式)简捷地解决问题.
1 挖掘背景构造,让解题思路明晰
许多问题的编拟都有一些特定的背景,要么是某个概念或数学公式,要么是某个已经解决了的实际问题,要么是一个基本思想的应用等[3].有些问题,当孤立地运用题设条件难以获得解题思路时,不妨把所考虑的问题置于特定的背景下,构造原题的原形,往往可得到简捷巧妙的解法.构造法往往要通过仔细观察、分析,去发现问题各个环节以及其中的联系,从而为寻求解法创造条件,因此构造法体现了发现的思想.
例1已知a,b,c,x都是实数, 且a 分析x-a的几何意义是,在数轴上表示x与a两数之间的距离,因此要求x-a+x-b+x-c的最小值就是要在数轴上找一点x,使其到a,b,c的距离之和最短.当x取在b以外的地方时,三条线段x-a,x-b,x-c都有重叠部分,所以当x取在b点时x-a+x-b+x-c有最小值,最小值为c-a. 分析构造数列模型 所以数列{an}为递增数列. 故an>0(其中n∈N+),即原不等式得证. 对于某些关于自然数的不等式问题,与数列有着密切的联系,这时可构造有关数列模型,利用其单调性解决.具体地说,欲证含有与自然数n有关的不等式f(n)>g(n),可以构造数列模型an=f(n)-g(n),证明数列{an}是单调递增,且a1>0.当然本题也可以用数学归纳法或其它方法进行证明,但相比之下,用构造数列模型去证,显然更为简洁. 分析由题设条件,可以作一个三度(长度、宽度和高度)分别为cosα,cosβ,cosγ的长方体,原问题就可以建立在这个长方体内进行讨论和证明了. 图1 由于长方体一条对角线和与它过同一顶点的三条棱所成角的余弦值的平方和等于1,为此可构造一个长方体ABCD-A1B1C1D1,如图1所示,使∠C1AD=α,∠C1AB=β,∠C1AA1=γ.设AD=a,AB=b,AA1=c,则 由基本不等式,得 数形结合是数学中常用的思想方法.在解题中,数与形的转换经常用到.通过数形结合,构造某种数学形式,使条件与结论的关系很简洁明了的展现出来,直观、具体,从而使问题得到解决. 图2 例4证明sin 5°+sin 77°+sin 149°+sin 221°+sin 293°=0. 分析此题若作为“三角”问题来处理,当然也可以证出来,但从题中的数量特征来看,发现这些角都依次相差72°,联想到正五边形的内角关系,由此构造一个正五边形,如图2所示. 这里,正五边形作为建模的对象恰到好处地体现了题中角度的数量特征.需要解题者具有敏锐的观察力与想象能力.如果没有一定的建模训练,是很难“创造”出如此简洁、优美的证明的. >sin2x+sin2y+sin2z 分析先化简结论得 即 图3 分析此题用常规方法求解,较为繁琐,转换思维视角,依条件构造解几模型,可获得新颖别致的解法.将原函数式变形为 图4 构造法体现了类比的思想,为了找出解题途径,要联系已有知识中与之类似的或与之相关的问题,从而为构造模型提供参照对象.数学解题时,不妨先看看比比,察觉面对的问题与头脑中的“已知”之间在结构、规律等方面的相似因素,通过联想,类比构造出数学模型,找到解决问题的路径. 分析此题x,y分离在两个等式之中,看似无从着手,但深入研究已知条件,可以发现两个等式有一些相似的地方.事实上,把第二个等式进行适当变形可得: (2y)3+sin 2y+2a=0, 与x3+sinx-2a=0相比较,容易发现两式结构相似,x和2y居于相同的“角色”.自然想到构造函数f(x)=x3+sinx,则两个条件分别变为: f(x)=2a和f(2y)=-2a,即f(x)=-f(2y), 因为函数f(x)=x3+sinx是奇函数, 所以有f(x)=f(-2y), f(x)是单调递增的函数, 所以有x=-2y,即x+2y=0, 因此,cos(x+2y)=1. 主成分分析也称主分量分析,旨在利用降维的思想,把多指标转化为少数几个综合指标。在用统计方法研究多变量问题时,变量太多会增加计算量和增加分析问题的复杂性,人们希望在进行定量分析的过程中,涉及的变量较少,得到的信息量较多。希望用较少的变量去解释原来数据中的大部分变量,将许多相关性很高的变量转化成彼此相互独立或不相关的变量。通常是选出比原始变量个数少,能解释大部分数据中变量的几个新变量,即所谓主成分,并用以解释数据的综合性指标。本文应用SPSS软件针对表1所列15个指标应用主成分分析法分析,以找出15个指标中的内在联系,并加以总结归纳。 通过化简去掉了根号,即 构造法还体现了化归的思想,表现在把一个个零散的发现由表及里、由浅入深地集中和联系起来,通过恰当的方法加以处理,化归为已有的认识,自然形成了构造模型的方法.事实上,有些问题生疏隐晦,按其本来面目无从入手.这时,解题者应充分把握问题的本质,并对问题作一番提炼、抽象与纯化,对其进行恰当赋义,化归为一个全新的数学问题.新的数学问题往往超越了原问题的背景或意境,提供了更广阔的思维空间,为问题最终获得解决架设了一条通道. 所以函数的最大值为2,最小值为0. 可以看到,利用三角函数性质进行构造,可以巧妙地摆脱问题中根号带来的困惑. 例11从6对老搭档运动员中选派5名出国参赛,要求被选的运动员任意两名都不是老搭档,求有多少种不同的选派方法? 图5 分析构造六棱柱ABCDEF-A1B1C1D1E1F1,如图5所示,用6种不同的颜色给六棱柱的12个顶点染色,使得同一侧棱的两端点同色,用来表示一对老搭档运动员.于是问题被巧妙地化归为:求从12个着色点中任取5个不同色的点的不同取法即可.这可分两个步骤完成: 故由分步乘法计数原理,完成这件事共有6×32=192种方法,即选派5名运动员共有192种方法. 例12求r元方程x1+x2+…+xr=n非负整数解的组数. 分析解决这个问题,我们可以设计一个适当的数学问题模型,把问题直接化归到不重组合问题上,即: 把n个不加区分的球全部放入r个盒子里,每个盒子内的球数不限,也可以有空盒子,共有几种不同放法? 设想n个球放在一条直线上,如图6所示,在两边插上固定挡板A、B.然后利用r-1个活动板插入球与球或球与挡板之间的空隙(例如C、D、E…).我们把从A板开始的每相邻两个挡板间的球数顺次记为x1,x2,…,xr.这就是方程的一组解. 图6 构造法解题的非常规性与创造性,使得常常需要非逻辑思维的参与,才能取得关键性的进展[5],因此,直觉、灵感、想像等思维活动在构造解题中往往不可或缺. 同时,上述构造策略的揭示与方法的选取,也只是为了讨论问题的方便,具体解题时还需综合考虑问题本身相关的多个因素.有的问题可以直接构造,有的则需要间接构造;有的需要构造条件,有的则需要构造反例;有的要考虑图形的构造,有的则着力于变量间关系的构造.总言之,构造法解题并无定法,或许还要渗透着猜想、试验、归纳、类比、分类等基本的问题解决策略.然后,构造法却也是有规律可循的,相信通过深入剖析问题所给背景与结构,灵活采用数形结合、建模化归等数学思想,借助于构造法,一定会突破思维瓶颈,为顺利快捷地完成解题任务创造有利的条件,奠定坚实的基础.

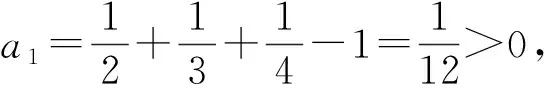
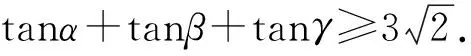


2 数形转换构造,让解题云开雾散
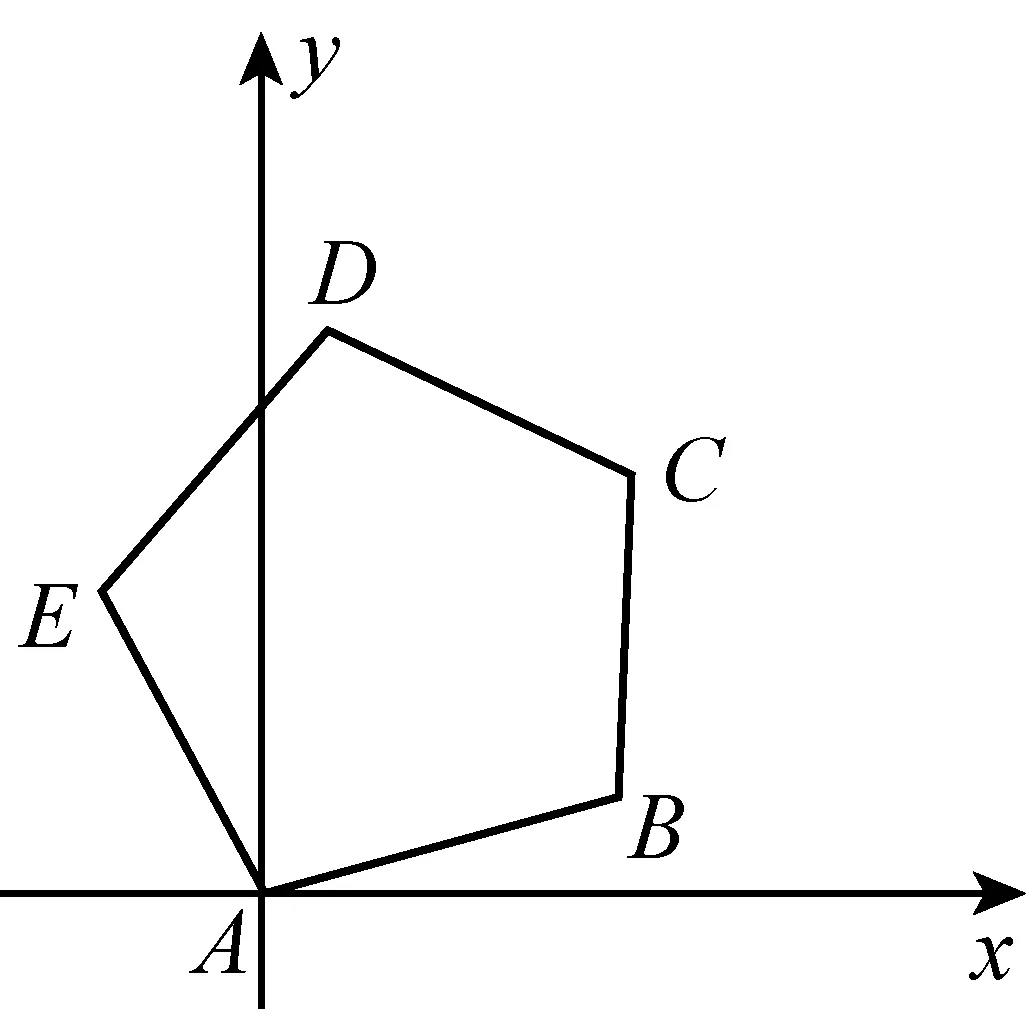
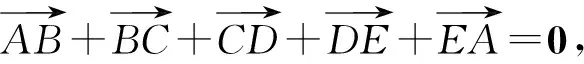

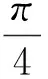
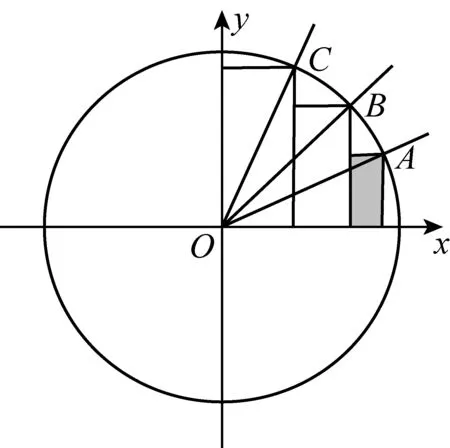

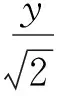
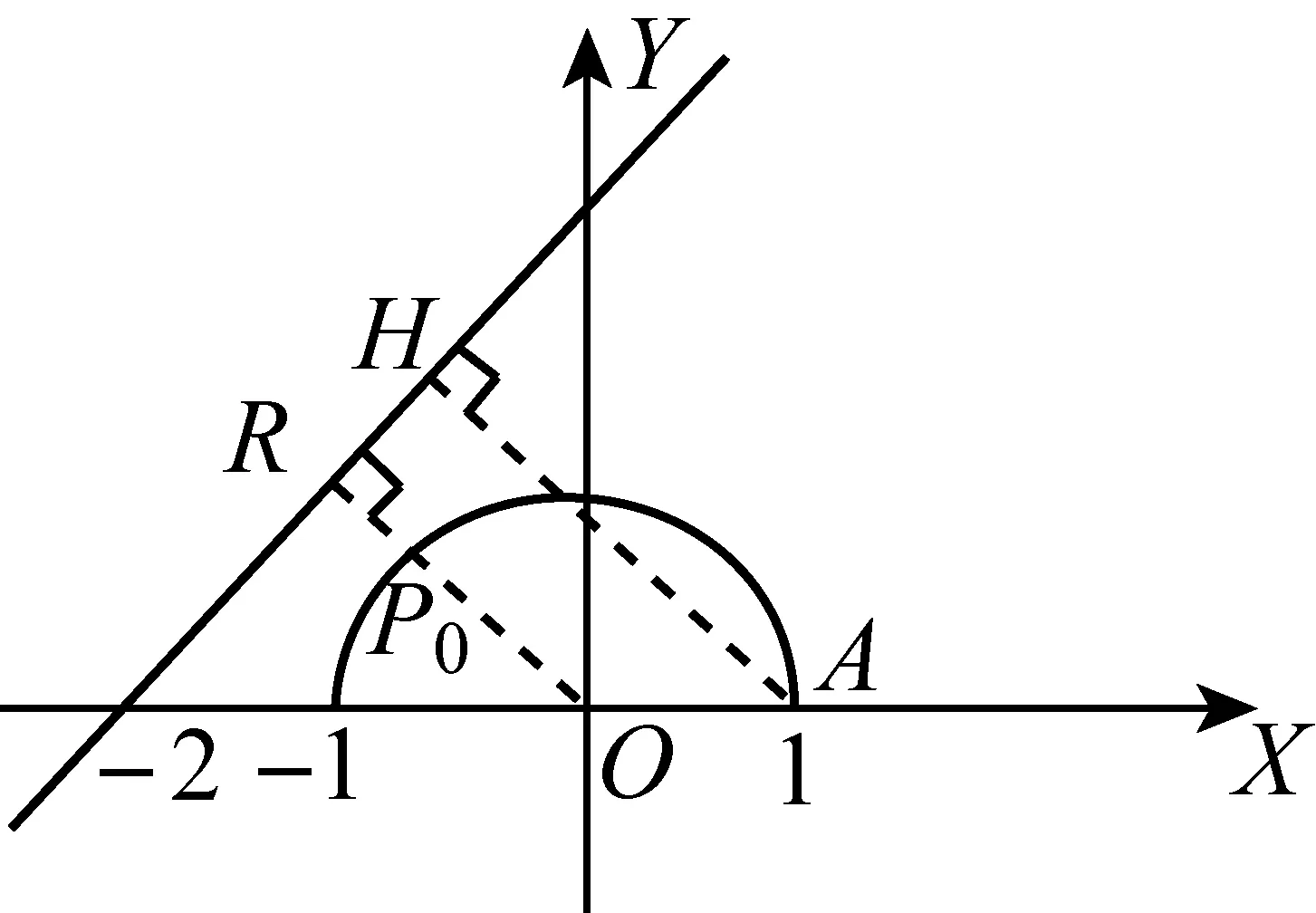

3 透析结构构造,让解题触类旁通
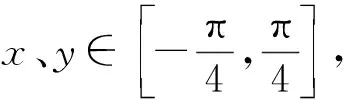
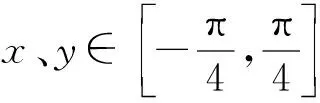




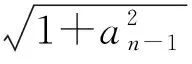

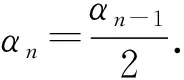
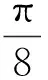
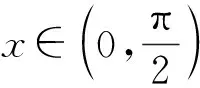
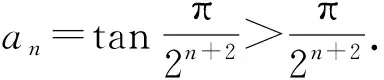
4 运用化归构造,让解题冲出重围