旋转坐标系下分区计算的LU隐式方法

肖中云，刘刚，牟斌，江雄

中国空气动力研究与发展中心 计算空气动力研究所，绵阳 621000

当前CFD并行计算大多采用区域分解的并行算法，将计算域按照负载平衡原则分配给不同进程，每个进程分别采用时间推进方法进行迭代求解，并通过进程间消息传递交换流场数据。这种方法由于信息交换量小、负载平衡性好而得到广泛使用。严格地说，隐式时间迭代算法由于在分区边界存在依赖关系并不能直接用于并行，通常这种影响量很小而被忽略。但是这样的简化在旋翼计算中却碰到了收敛性变差的问题，甚至导致一些非物理的计算结果。出现这样的问题与旋翼流动特点有关，旋翼以旋转运动为主，在悬停和低速前飞状态下，旋翼尾迹旋绕桨盘附近，向远场的发展过程缓慢。由于流动的这种特性，数值计算误差容易被积累，导致收敛性变差[1-3]。随着并行计算规模的增长，旋翼CFD计算对算法的可扩展性提出了很高要求，这就需要发展考虑分区边界影响的隐式时间迭代格式，对忽略边界影响的处理方法进行重新评估，目的是使大规模并行计算不会因为进程数增加导致收敛性变差或者失效，同时计算结果不受进程数目的影响。

文献[4-5]对计算流体力学的并行计算技术进行了综述，指出显式格式是内在并行的而且并行网格划分不影响其数值特性，保持串、并行计算过程一致。常见隐式格式中雅克比松弛是内在并行的，高斯-赛德尔松弛与其他线松弛格式由于网格点相互依赖，非内在并行，但通常有更好的收敛性。由于这类方法的并行求解比较困难，实际计算中通常采取“局部隐”的方法，即对计算区域进行分块，对每块独立进行隐式求解，块边界值由相邻块前一时刻的值来确定。

基于LU分解的对称高斯-赛德尔(LU-SGS)迭代是一种典型的隐式时间迭代算法[6-7]。Wissink等[8]最早提出了原始LU-SGS时间迭代方法在分区边界会产生误差，尤其在并行规模较分区边界较多时误差得到放大；提出了基于雅克比迭代的数据并行LU松弛算法(DP-LUR)，同时将LU-SGS与DP-LUR进行结合构造了混合LU-SGS方法(HLU-SGS)，提高了收敛效率。Luo等[9]在对HLU-SGS方法进行研究以后，认为当网格块数较多时，混合方法具有优势，当并行规模较小时边界数据传递不会对结果带来影响，由于LU-SGS具有较高的迭代效率，在计算中直接采用了LU-SGS方法进行并行计算。Otero和Eliasson[10]将LU-SGS直接应用于并行计算，采用多次迭代的方法，在每一次前向扫描和后向扫描完成后分别进行一次消息传递接口(MPI)交换信息，更新边界单元的ΔQ值。文中称这种方法为混沌更新，利用多次迭代消除未按顺序更新带来的误差。

目前在旋翼计算中隐式时间迭代方法得到了广泛应用，但是关于分区边界影响的研究较少。文献[11]在非惯性旋转坐标系下对旋翼悬停状态进行了模拟，时间离散采用的LU-SGS隐式迭代方法，在两次扫描过程中，虚拟单元上的值直接赋零。文献[12-13]在惯性系下对旋翼前飞状态进行并行计算，时间推进采用隐式LU-SGS格式，但对并行计算的边界如何处理没有进行特别说明。针对旋翼并行计算中隐式时间迭代方面的潜在问题，本文在同一框架下发展了LU-SGS、DP-LUR和HLU-SGS计算方法，分析了原始LU-SGS方法在并行计算中产生误差的行为及原因，通过在旋转坐标系下静止场计算验证了算法的有效性。在此基础上，采用分区并行计算、多重网格方法等先进算法对旋翼的悬停流场进行模拟，获得了较高的并行效率和流场计算精度，进一步验证了本文方法对于大规模分区计算的适用性。相关方法可以进一步推广到其他流动问题的旋转坐标系计算。

1 数值计算方法

1.1 LU-SGS时间隐式迭代格式

Navier-Stokes方程经过隐式时间离散后的形式为[6]

(1)

式中：Q为守恒型流场变量；R为Navier-Stokes方程右端项；V为单元控制体体积；Δt为时间步长；下标i为单元编号；上标n为当前时间步。为了得到左端的雅克比矩阵，通量函数采用最大特征值分裂，即

λij(Qj-Qi))sij

式中：F为通矢量；j为单元i的相邻单元；sij为交界面面积；nij为单位法向矢量；λij为通量雅可比矩阵的谱半径，λij=|vij·nij|+cij。

将左端雅克比矩阵分解为上三角矩阵U、下三角矩阵L和对角阵D这3个部分，得到

(2)

式中：

其中：N(i)为单元i的相邻单元；L(i)为左相邻单元；U(i)为右相邻侧单元；由于控制体封闭[14]，单元i满足：

得到

同时用到

LU-SGS算法首先对式(2)进行近似分解，然后采用高斯-赛德尔迭代求解线性代数方程，即

(D+L)D-1(D+U)ΔQ=R

1) L扫描

(D+L)ΔQ*=R

2) U扫描

(D+U)ΔQ=DΔQ*

式中：ΔQ*为L扫描后得到的流场变量值；ΔQn+1为U扫描后得到的流场变量值。MPI并行计算采用域分解的算法，高斯-赛德尔迭代在域边界位置会碰到相邻点流场值无法及时更新的问题。图1 给出的是二维网格LU-SGS迭代的L扫描示意图。当扫描到边界单元时，位于其左侧或下侧相邻单元的当前时刻值(ΔQ*)不可用，通常只能进行简化处理，如假设ΔQ*=0，这种简化带来的误差在特定情况下可能放大，引起计算不稳定或者发散。在并行计算分区数很大时，对边界的处理方式要谨慎对待。

图1 LU-SGS格式L扫描示意图Fig.1 Diagram of lower sweep in LU-SGS scheme

1.2 基于LU分解的时间迭代并行计算方法

由1.1节可见，高斯-赛德尔迭代方法在并行分区边界会碰到问题，无法做到与串行计算结果一致。而在本质上，DP-LUR方法将离散方程式(2) 的非对角项移到方程的右边，用Jacobian迭代代替对称Gauss-Seidel迭代。这样DP-LUR方法对当前时间层的流场值没有依赖，保证了计算域内部单元和边界单元采用完全相同的计算格式推进。DP-LUR算法的收敛效率低于LU-SGS算法，通常将迭代次数取为5步甚至更多。

ΔQ0=D-1R

Dok=1,2,…,ksweep

ΔQk=D-1[R-(U+L)ΔQk-1]

End Do

ΔQn+1=ΔQksweep

为了同时利用LU-SGS迭代的高效率和DP-LUR在边界处理上的优点，文献[8]发展了两者相混合的方法(HLU-SGS)，即在块边界单元采用Jacobian迭代格式，计算边界单元的ΔQ，随后对所有采用LU-SGS方法进行计算，对于块内部单元来说，算法等同于LU-SGS方法；对于块边界单元来说，相邻单元的ΔQ为已知的当前时刻的值。在极限情况下，当所有单元都是边界单元的情况时，该计算格式退化为点隐式的Jacobian迭代方法。HLU-SGS的算法为

ΔQ0=D-1R

Dok=1,2,…,ksweep

边界信息交换ΔQ*(k)=ΔQ(k-1)

采用Gauss-Seidel方法计算ΔQ(k)

End Do

ΔQn+1=ΔQ(ksweep)

图2给出的是多块结构网格的计算流程图，其中MGCycle表示多重网格循环，BLK表示网格块号，P1、P2、PM表示进程编号。可以看到每进行一次时间步迭代，各进程间只进行一次通信，交换网格边界的的流场信息。在每个计算进程内，各网格块之间相对独立，为了节省内存开销，大部分工作变量都定义在当前网格块上，包括流场变量、网格度量系数、右端项残差等，在完成当前块计算以后，这些数据被下一网格块取代。

并行隐式时间迭代算法的流程图如图3所示，从图中可以看到，各网格块之间的计算相互耦合，比如在每次进行时间迭代时，需要对所有网格块进行扫描，并进行进程间通信，交换网格边界流场解ΔQ信息。显然，在上述需求下，原来的基于单块的数组存取方式不再适合。本文的改进方式如下：取消基于单块网格的数组变量，用一维数组存放当前进程下所有网格的流场变量；开辟全局数组存放网格的几何度量系数信息，这些信息在右端项计算和时间迭代计算中将要用到；开辟全局数组存放右端项残差，该信息在DP-LUR迭代和LU-SGS 迭代中将分别用到。在经过上述改进以后，在同一计算框架下，既可以完成原有的LU-SGS迭代计算，也可以进行多次内迭代的DP-LUR计算，还可以进行DP-LUR和LU-SGS的混合计算。

图2 网格分区并行计算的原有流程Fig.2 Original flow chart of grid partitioned parallel computation

图3 网格分区并行计算的改进流程Fig.3 Improved flow chart of grid partitioned parallel computation

1.3 并行程序设计

并行网格分配采用贪婪优化算法，其核心思想是：将当前最重的任务，分配给当前负载最小的进程[15]。当原始网格分布不满足分配要求时，需要对网格块进行剖分，根据贪婪算法的设计思想，在找到当前最需要网格的进程和当前最大网格块之后，如果网格块单元数小于或刚好等于要求的网格单元数时，则直接将该网格块放到该进程。但更多时候是，当前网格块单元数大于所需的网格单元数，就需要对当前网格块进行拆分。采取的拆分策略是：当网格块的剖分位置位于维数25%～75%之间时，对网格进行按需剖分并分配；当剖分位置不在25%～75%范围内时，对网格块进行中位剖分，剖分后不分配，继续查找当前最大网格块进行下一步操作。负载平衡与边界单元数最少是结构网格剖分的一对矛盾，为了使网格块不被分得过于零碎，同时也减少分区边界数，要牺牲一些负载平衡要求，一般将负载不平衡度控制在5%～7%以内可以取得较好的剖分结果。并行网格分配的另一项重要任务是建立分区边界的映射关系，确定出发送/接收次数，以及每次发送/接收的对方进程号、字段长度、相对应的网格单元编号等信息。

图4 MPI并行的编程模型Fig.4 Model for MPI parallel programming

并行程序设计采用对等模式，如图4所示，每个进程地位相同，代码和功能基本一致，只不过是处理的数据对象不同。由于边界点新值的计算需要相邻边界其他块的数据，因此在每一个数据块的两侧各增加1列数据空间，用于存放从相邻数据块通信得到的数据，进程之间通过MPI发送与接收函数进行消息传递。

为了适应多重网格计算，网格单元按照原始网格、第2重网格、第3重网格等的顺序进行排序，并存储在一维数组当中，每一重网格计算分别是对数组中的某一段进行操作。假设当前进程的原始网格单元为N，那么多重网格的次密层单元数为N/8，第3重为N/64，以此类推。对任意网格点来说，由多重网格层数、网格块号、3个方向的指标号(i,j,k)可以确定出唯一指标号，即在一维数组中的存放位置。假设任意流场变量A，在进行多重网格计算时，每一重网格上的数据分别为

第1重网格：A(1:N)

第2重网格：A(N+1:N+N/8)

……

上述数据存储结构中只考虑了计算单元，没有考虑虚拟边界单元。当计算每一个具体的网格块时，另开辟专门的边界数组进行存储虚拟单元的流场变量值。如图5所示，“i”方向的边界数组可以表示为“Boundi(1:2,jdim,kdim)”，其中“1，2”分别代表左边界的两排虚拟单元，“3,4”代表右边界的两排虚拟单元，jdim和kdim表示边界面j和k方向上的网格维数。

图5 网格块与虚拟边界单元Fig.5 Grid block and virtual boundary cell

2 计算结果与分析

2.1 旋转网格算例测试

根据动网格计算对“均匀流保持特性”的要求[16]，设计了如下算例，即取静止流场中的一块网格，采用动网格方法对流场进行模拟，无论网格做何种运动，最终得到的结果都应该是保持静止初场不变。如图6所示，取计算域为周向角等于36°的一块扇形网格，假设参考长度(旋翼展长)为R，网格的周向远场边界为4R。采用静止流场作为初场，经过任意长时间的计算后，流场应保持初场不变，即流场状态变量与环境变量相等，用密度或其他变量表示的流场残值应该保持为机器零值。

计算在旋转坐标系下进行，旋翼桨尖马赫数Matip=0.352。由于计算域为没有旋翼的空流场，远场为静止大气，边界条件采用无反射黎曼边界条件，采用静止流场作为初场，空间离散采用Roe通量差分格式，库朗数(CFL数)取为20。首先对单块网格的串行计算进行了测试，结果表明，在当前参数设置下计算可以顺利进行，密度残差一直保持在机器零值(实数用双精度表示，机器零值约为10-16)。

并行计算采用8个分区，网格划分方式分为两种，一种是沿展向划分，一种是沿周向划分(见图6)。为了考察分区边界对数值计算的影响，分别对3种时间离散方法进行了对比，一种是LU-SGS 方法，每个时间步分别进行一次L扫描和U扫描；一种是DP-LUR方法，该方法由于迭代效率较低，在每个时间步的内迭代步数为8步；一种是HLU-SGS方法，该方法结合了LU-SGS和DP-LUR方法，每个时间步进行2次DP-LUR迭代和1次LU-SGS迭代。需要进一步指出的是，由于DP-LUR方法采用雅克比内迭代，文献[8]认为5次内迭代可以获得与高斯-赛德尔迭代类似的收敛速度，本文测试结果表明，DP-LUR方法采用8次内迭代，HLU-SGS方法采用2次DP-LUR迭代和1次LU-SGS迭代可以获得很高稳定性，使周向边界取20倍旋翼半径、CFL=10 000情况下保持计算稳定。综合上述因素，建议DP-LUR方法内迭代次数选取为5～8次，HLU-SGS方法的DP-LUR内迭代次数为1～2次。

图6 展向和周向网格剖分示意图Fig.6 Schematics of spanwise and circumferential grid partitions

图7给出的是2种剖分网格、3种隐式时间迭代方法得到的残差变化曲线，其中残差用密度的L2模表示，Span8表示展向分为8个分区，Circum8表示周向分为8个分区。从图中可以看到，对于DP-LUR格式而言，无论网格是周向剖分还是展向剖分，密度残差一直保持为机器零值，即网格运动没有引起流场发生变化，流场保持为静止初场。对于LU-SGS格式来说，展向剖分网格对应的流场随迭代步数不变，但是对于周向剖分网格，随迭代步数密度残差增大，流场不再是理论上的静止流场。为什么是周向划分网格导致计算发散呢？对于当前旋转运动网格来说，周向剖分网格的边界方向与旋转方向相同，边界面上的逆变速度(流体相对于网格坐标的速度)大，也就意味着面上的流通量大。当LU-SGS格式用于上述网格的并行计算时，由于其在边界上的简化处理，方程中起主导作用的物理量被丢掉，导致了误差放大和计算发散。相对而言，HLU-SGS和DP-LUR格式在时间迭代中增加了边界上的信息交换，对两种剖分网格的计算都得到了收敛结果。

图7 3种格式、2种网格下的残差历程(CFL=20)Fig.7 Residual histories of three operators applied to two grids (CFL=20)

针对图7中的发散算例(对应周向剖分网格)，图8为采用不同CFL数计算得到的残差曲线。从图中可以看到，在迭代2 000步前提下，LU-SGS格式CFL=20对应的密度残差发散最快，CFL=10对应的曲线次之，CFL=5对应的曲线在计算时间内仍一直保持收敛状态，后续计算会不会发散未知。由此可见，这种由计算格式带入的误差十分危险，可能是以一种不易察觉的方式使计算结果受到污染。对于HLU-SGS格式来说，每个时间步采用2次DP-LUR迭代和1次LU-SGS迭代的组合方式使计算格式非常鲁棒，在CFL=10 000情况下计算仍保持收敛。

从前面分析可以看到，造成计算不稳定的原因来自于网格分区边界的运动速度，在旋转坐标系下该最大速度取决于转速和远场边界的大小。下面测试保持旋转速度不变，将远场边界与旋转中心距离b从4R分别增大到10R和20R，对应周向网格运动速度为1.41、3.52和7.04倍声速。图9给出的是不同计算域大小对收敛性的影响，其中时间推进为HLU-SGS格式，CFL=10 000。从图中可以看到，在远场边界不断增大的情况下，HLU-SGS计算格式都达到了收敛状态，显示了良好的计算稳定性；另外随着远场边界的增加，残差量级增大，在远场边界为20R时残差只能收敛到10-14量级，说明旋转坐标系计算远场边界不宜取过大。

图8 CFL数对残差曲线的影响Fig.8 Effects of CFL number on residual histories

图9 计算域对残差曲线的影响(HLU-SGS)Fig.9 Effects of computational domain on residual histories (HLU-SGS)

2.2 Caradonna-Tung标模旋翼计算

为了测试当前的计算方法，选择标准模型Caradonna-Tung旋翼[17]进行了悬停状态计算。该旋翼包括两片等弦长无扭转的桨叶，翼剖面形状为NACA-0012翼型，桨盘半径为1.143 m，桨叶展弦比为6。模拟状态桨尖马赫数Matip=0.44，总距θc=8°。网格采用重叠网格方法，包括桨叶网格和背景网格，背景网格又分别生成了稀/密程度不同的两套网格，其中稀网格3个方向的维数为109×119×165(对应径向、周向和法向)，桨尖区域的最小网格间距为0.05倍弦长，网格单元数约200万；密网格3个方向的网格维数为305×177×969(对应径向、周向和法向)，如图10所示，将桨叶展向0.65R～1.1R范围并且桨叶下方区域作为桨尖涡模拟区对网格进行均匀加密，网格间距为0.02倍弦长，网格单元数超过5千万。计算采用256个分区的并行计算，为了达到负载平衡要求，网格经过了多次剖分，剖分后的稀网格为452块，密网格为448块，图10显示了背景网格在经过网格剖分后产生的分区边界。

图10 稀/密网格的并行分区Fig.10 Grid partitions of coarse and fine grids

计算参考系为原点位于旋翼中心的旋转坐标系，只需模拟单片桨叶，周向采用周期性边界条件，远场边界采用悬停源/汇边界条件[18-19]。流动假设为全湍流，湍流模型为两方程k-ω剪切应力输运(SST)模型，空间离散采用Roe通量差分格式。时间迭代分别采用了原始LU-SGS方法、数据并行的DP-LUR方法与混合方法HLU-SGS，其中DP-LUR方法每个时间步进行6次内迭代，HLU-SGS方法每个时间步进行1次DP-LUR迭代和1次LU-SGS迭代。前面提到原始LU-SGS方法有计算不稳定的情况发生，为了对比3种计算方法，这里选择采用较小计算域和低CFL数方法，使3种隐式格式都能够正常计算，具体为背景网格的周向边界距离旋翼轴3倍旋翼半径，CFL=20。此外，为了加速收敛，计算还采用了V循环的多重网格方法和低速预处理方法，计算目标是使流场达到充分收敛。

流场收敛性研究与格式比较在稀网格上进行，为了充分让流场收敛，总迭代步数达到10万步。图11给出的是拉力系数CT/σ随迭代步数的变化，其中CT表示用桨盘面积无量纲化的拉力系数，σ表示旋翼实度，可以看到3种隐式算法中DP-LUR收敛最快，其他两种方法相当，HLU-SGS略快于LU-SGS方法。由于DP-LUR方法在一个时间步内进行了6次迭代，其收敛快是可以预料的，HLU-SGS方法在一个时间步数内进行了1次DP-LUR迭代和1次LU-SGS迭代，收敛略快于原有的LU-SGS方法。

由于3种方法每个时间步的计算时间不同，为了比较各自的收敛速度，图12给出了拉力系数CT/σ随时间的变化曲线，可以看到原始的LU-SGS方法收敛速度最快，DP-LUR方法收敛速度最慢，尽管HLU-SGS方法相对原始LU-SGS方法计算量有增加，这是边界隐式计算所付出的代价，但是相对DP-LUR方法计算效率有了明显提高。

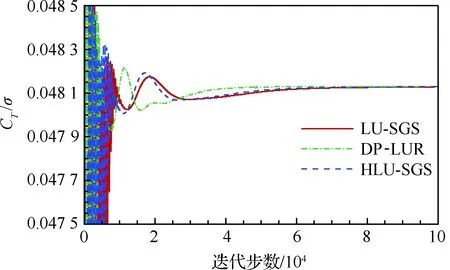
图11 拉力系数随迭代步数的变化Fig.11 Variations of thrust coefficient with iterations

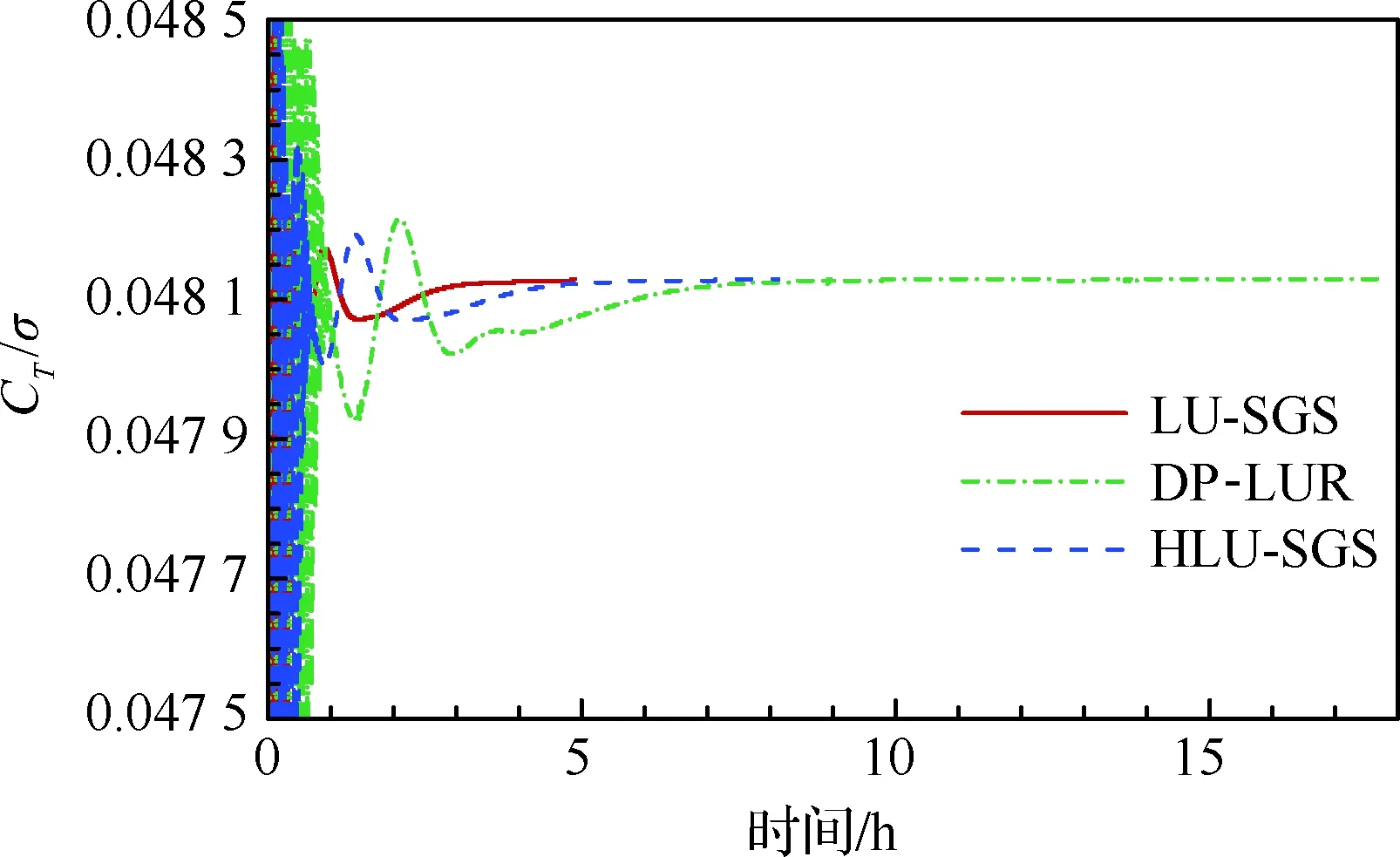
图12 拉力系数随时间的变化Fig.12 Variations of thrust coefficient with time

图13给出的是并行计算的加速比和并行效率统计，在高性能计算机系统上完成计算，每个计算节点采用Intel Xeon处理器(64核，256 G共享内存)，结点之间采用无限带宽技术(Infiniband)高速互连。测试算例为密网格算例(网格单元数约5千万)，在同样计算条件下分别采用了1～512核进行了计算，由于所测得的数据有一定的散布，图中除了给出每个算例的测试结果外，还用曲线进行了拟合。从图中可以看到，在测试范围内，随并行规模的扩大，加速比单调增大，但并行效率呈下降趋势。以128核并行计算为例，加速比约为94.5倍，并行效率约为74%。由于本文采用了并行隐式时间迭代方法，相对原始LU-SGS方法，在每个时间步增加了一次信息交换(传递ΔQ值)，通信需求的增加使并行效率有一定下降。

图13 并行计算的加速比与效率Fig.13 Speedup ratio and efficiency of parallel computations

图17给出了稀/密两套网格的截面流线和下洗速度云图比较，可以看到两套网格得到的下洗场分布比较一致，最大下洗速度约为15 m/s。不同之处是密网格刻画了更多的流动细节，包括旋翼尾迹中桨尖涡的分布，以及由于桨尖涡的存在使局部流线发生卷曲等。另外，值得注意的是，密网格计算得到的第一个桨尖涡的强度大于稀网格，旋涡引起的局部上洗速度大于15 m/s，由于旋涡位置靠近桨叶，将对桨叶气动性能的预测产生影响。

图14 拉力与扭矩系数的收敛曲线Fig.14 Convergence histories of thrust and torque coefficients

图15 Q值等值面Fig.15 Iso-surface of Q value

图16 稀/密网格的涡量云图比较Fig.16 Comparison of vorticity contour of coarse and fine grids

图17 截面流线和下洗速度云图Fig.17 Surface streamlines and down wash velocity contour

图18给出的是桨尖涡运动轨迹的计算值与试验值比较。从图中可以看到，密网格模拟的桨尖涡下降轨迹与试验值吻合一致，稀网格则过高估计了桨尖涡下降速度；从桨尖涡向内收缩来看，计算与Caradonna和Tung的试验值[17]存在较大差异。原因分析如下，本文计算只模拟了旋翼桨叶，不包括桨毂和旋翼轴；试验数据取自1981年Caradonna和Tung的试验，试验装置不仅有旋翼轴，还有测压管线沿旋翼轴引出，使旋翼轴体偏大，目测半径有5%～10%倍旋翼半径，中心轴体部分会影响桨尖涡向内收缩的偏移量，定性地说中心轴体增大，桨尖涡向内收缩量减小。图18同时参考了Kocurek的尾迹模型数据[17]，与本文计算结果比较一致，一定程度上验证了本文计算。总的来说，当前密网格计算获得了旋翼悬停流场的主要流动特征，在旋翼气动性能预测上更有优势，通过采用适用于分区计算的LU隐式方法改进以后，稀网格和密网格都获得了充分收敛流场，进一步验证了本文的并行分区算法。

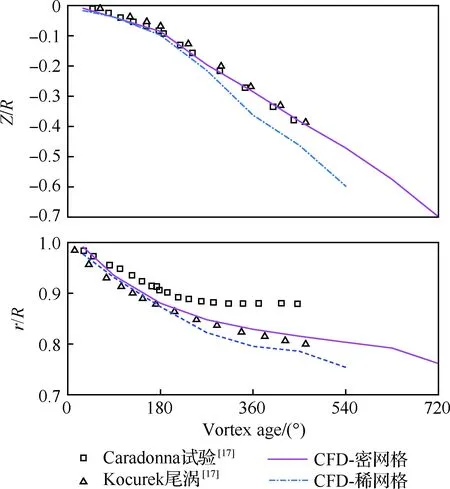
图18 桨尖涡的运动轨迹Fig.18 Trajectories of blade tip vortex motion

3 结 论

本文采用3种基于LU分解的隐式时间迭代算法，基于网格分区和基于MPI的并行方法，在旋转坐标系下对单独旋转网格、旋翼的悬停状态进行了数值模拟，研究了不同时间迭代格式对旋翼计算收敛性的影响。

1) LU-SGS隐式时间迭代方法由于在分区边界缺少相邻单元的流场信息，理论上如果直接应用于并行计算会在边界上带来误差，一般认为这种误差量很小、对结果没有显著影响。本文通过旋转网格算例证明，将LU-SGS方法应用于旋转网格并行计算时，当分区边界与旋转方向同向时，时间离散产生的误差会起主导作用并不断积累放大，使计算结果受到污染，并导致计算发散。

2) DP-LUR方法用雅克比迭代代替高斯-赛德尔迭代算法，避免了分区边界的迭代误差问题，能消除并行剖分对计算的影响，不足之处是每步时间推进需要进行多次迭代，计算效率低于LU-SGS方法。HLU-SGS方法是DP-LUR与LU-SGS两种方法的结合，能有效消除分区边界的影响，同时获得较高的计算效率，是一种适用于并行的隐式时间推进方法。算例表明该方法能很好适用于旋转坐标系下的旋翼计算，能够获得气动力与尾迹流场都充分收敛的计算结果。

3) 本文讨论的隐式时间迭代方法适用于所用旋转坐标系计算，解决了结构网格多块分区和并行计算分区的问题，适合于计算域较大和网格整体旋转的情况。除旋翼悬停计算以外，该方法还可以推广到飞机的绕速度矢滚转、螺旋桨、风力机等其他旋转类流场的数值计算。