复合材料梁弹性参数不确定性量化及试验验证
吴邵庆 范 刚 李彦斌 姜 东 费庆国
(1东南大学土木工程学院, 南京 211189)(2东南大学空天机械动力学研究所, 南京 211189)(3东南大学机械工程学院, 南京 211189)
纤维增强复合材料具有比强度高、比刚度大、抗疲劳性能好等优点,在航空航天、机械等领域得到广泛应用[1].该类复合材料由于内部纤维、基体、界面特性、复杂加工工艺等[2],其宏观力学参数存在明显的离散性.建立准确的纤维增强复合材料结构力学模型,需要对其力学参数中的不确定性进行定量评估.
针对纤维编织复合材料等效宏观弹性参数的不确定性研究,大多采用代表性体积单元与有限元相结合的方法[3-6].由于复合材料细观结构的微小变化均需要重新划分有限元网格,利用基于细观有限元模型来研究细观参数分散性对复合材料宏观性能的影响,计算效率非常低,且无论细观建模如何精细,仍与实际材料存在误差.为更高效地量化复合材料等效宏观力学性能的不确定性,研究者们开展了基于随机场表征的复合材料参数不确定性量化研究[7-9].由于缺乏试验数据,上述研究都采用假设的随机场来模拟含不确定性的材料弹性参数,与实际复合材料参数的不确定性存在较大偏差.因此,开展基于试验数据的复合材料不确定性量化能够为复合材料结构提供更加准确全面的力学模型.
现有的复合材料参数不确定性量化方法主要集中在系统参数统计特征的识别方面.文献[10-11]利用混沌多项式分别展开正交异性板的不确定性参数和模态参数,利用板的固有频率样本拟合概率模型,进而由模态参数概率模型识别弹性参数的概率分布;文献[12-14]基于一阶摄动的随机模型修正方法,利用实测模态数据识别了复合材料板弹性参数的统计特征;Debruyne等[15]同时考虑了模态参数测量误差和材料弹性参数的不确定性,利用不确定性模态参数识别了蜂窝夹芯复合材料梁的弹性参数随机场;MacHado等[16]利用空间相关的随机分布场描述系统不确定性参数,基于灵敏度分析方法由实测频响函数样本识别了弹性参数的随机分布场.
本文针对纤维编织复合材料梁,开展了基于小样本试验数据的复合材料不确定性弹性模量的随机建模方法研究.该方法结合了小样本试验数据的先验信息,能够在实测样本数量小于50情况下,为含不确定性材料参数的复合材料结构的高精度动响应预示和动强度评估提供准确的随机参数量化模型.
1 不确定性参数的量化模型
采用Karhunen-Loève(K-L)展开方法可将随空间分布的梁弹性模量随机场E(x,θ)表示为确定性空间函数与随机变量乘积的线性组合[17].随机场的K-L展开是基于自协方差函数的谱分解,其特征值问题可表示为如下Fredholm积分:

(1)
式中,CFF为随机场的自协方差函数;λk和φk分别为CFF的特征值和特征函数.特征函数集{φk}在其定义域内构成一个完备正交基,则随机场E(x,θ)可以有如下K-L展开:

(2)


(3)


(4)

由于梁试件数目较少,式(3)中随机变量η(k)的分布特征无法确定,利用一维混沌多项式展开[18]来表示未知分布特征的随机变量η(k):

(5)

(6)
式中,Hα(ξk) 为归一化前的混沌多项式基,有如下递推关系式:
(7)
由于η=[η(1),η(2),…,η(v)]满足E[ηηT]=Iv×v,则有

(8)
将式(5)代入式(3),可得复合材料梁弹性参数随机场量化模型:

(9)

2 不确定性量化模型中混沌多项式系数估计


(10)



(11)


(12)
且

(13)

式(10)中建立了γ(k)的后验分布函数,然后采用Metropolis-Hasting采样算法[22]进行采样,得到目标分布的样本.Metropolis-Hasting采样算法步骤如下:
① 设置马尔可夫链的长度s和采样起始步tb,初始化当前状态条件γβ=γ1,设j=1.
② 由式(12)计算得到当前状态条件γβ下的似然函数L(γβ).
③ 采用随机高斯摄动ε~σεN(0,I),生成新状态条件γθ,并由式(12)计算新状态条件γθ下的似然函数L(γθ).
④ 定义接受概率ρ(γθ,γβ)为

(14)
⑤ 生成一个均匀分布的随机数u~U(0,1),如果u≤ρ(γθ,γβ),接受转移,即γβ+1=γθ;否则不接受转移,令γβ+1=γβ.
⑥ 重复步骤③~⑤,直至j=s.


(15)
式中,J(γ(k))为费舍尔信息矩阵(Fisher information matrix),定义其经验公式为

(16)


(17)
将式(13)代入式(17),可得
(18)
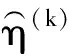
根据式(15),采用蒙特卡罗模拟依次抽样得到γ(k)=[γ1(k),γ2(k),…,γq(k)]的样本,代入式(9)建立弹性参数随机场的不确定性量化模型.弹性参数的样本直接反映了其分布特性,通过核密度函数法拟合可以得到其概率密度函数.
3 非均匀复合材料弹性参数不确定性量化
3.1 复合材料梁杨氏模量场识别
以C/C纤维编织复合材料梁为研究对象,开展同一批次多组梁的模态试验.
搭建如图1所示的模态试验系统,试件一端固支,有效尺寸为260 mm×15 mm×3 mm,均匀布置14个测点.采用单点激励多点拾振的方式开展模态试验.激励处为2号点,采用激光位移计对各测点处的动位移开展非接触式测量.根据激励信号和各测点处的动位移信号,计算得到各测点处的位移频响函数,利用小波去噪后,乘以频率的平方得到加速度频响函数.

图1 模态试验系统及试件
根据上述试验方案,依次开展23根复合材料梁试件的模态试验.图2中给出了各梁试件的同一测点(测点3)处的加速度频响函数(FRF).由图可知,在300~400 Hz,800~1 000 Hz两个区间范围内,同一批次的复合材料梁试件出现了对应第1阶和第2阶固有频率的峰值;同一批次不同梁试件的固有频率及其峰值均具有一定的离散性,表明材料参数存在不确定性.
由于试件长度方向尺寸远大于厚度和宽度方向尺寸,因此仅考虑复合材料梁长度方向弹性模量随空间分布的非均匀性.由于试件高跨比小于1/5,采用欧拉-伯努利梁模型,建立如图3所示的悬臂梁有限元模型.

图2 不同梁试件同一测点处的加速度频响函数

图3悬臂梁有限元模型
基于实测加速度频响函数,利用基于频响函数的复合材料空间分布模量场识别方法[25],依次识别获得23根复合材料梁有限元模型中各单元的杨氏模量,并将第i个单元的杨氏模量Ei(i=1,2,…,13)用随机变量描述,定义一维随机向量E(θ)=[E1(θ),E2(θ),…,E13(θ)].图4中给出了同一批次复合材料梁杨氏模量随机场E(θ)的样本,此时,样本总数M=23,随机变量个数N=13.
3.2 复合材料梁杨氏模量场不确定性量化


图5 K-L特征值相对累积和的收敛性(v=9)

图6混沌多项式系数γ(3)的后验样本分布直方图
图7混沌多项式系数γ(6)的后验样本分布直方图


(a) 单元1

(d) 单元4

(g) 单元7
4 不确定性材料参数量化模型试验验证
基于不确定性材料参数量化模型建立复合材料梁的谱随机有限元模型,开展确定性正弦激励下含不确定性参数结构的随机动响应预示,利用试验实测动响应的统计特征验证随机动响应预示结果的精度,从而证明不确定性材料参数量化模型的正确性.
将复合材料杨氏模量的不确定性量化模型代入悬臂梁有限元模型中,并在测点4处施加如图9中所示正弦激励,采用谱随机有限元方法(SSFEM)[26]计算各测点处随机动位移响应的均值和方差,结果分别如图10和图11所示.
搭建如图12中所示复合材料悬臂梁振动试验系统,通过激振器将图 8中的正弦激励信号施加在试件测点4处,采用力传感器和激光位移计分别测量激励和动位移信号,开展了同一批次23根复合材料梁在相同动载荷工况下的振动试验.将试验测量的各测点处动位移响应样本进行概率统计,获得其均值和方差,与采用谱随机有限元方法计算得到的动位移响应统计特性分别对比,结果见图10和图11.由图可知,计算均值与试验样本统计均值吻合较好,在动位移响应极值点处相对误差稍大.定义由谱随机有限元法计算得到的响应DSSFEM与试验测量得到的响应Dtest之间的相对误差RE为

图9 正弦激励信号

(c) 测点10
图10梁上各测点处动位移响应的均值

(a) 测点6

(c) 测点10
图11梁上各测点处动位移响应的方差

(19)
式中, ‖·‖2表示向量的2-范数.根据式(19),测点6,8,10,12处响应的计算均值和试验均值相对误差分别为7.4%,9.6%,11.2%,12.8%.由图11可知,采用谱随机有限元方法预测的各测点处响应方差曲线与试验统计结果均呈现吻合的振荡变化趋势,具有较好的一致性,2类结果均定量反映了正弦激励下由系统参数不确定性引起的结构动响应不确定性.计算方差与试验方差存在一定偏差,在极值点处的误差相对稍大,主要原因是:① 由本文提出的方法建立的不确定性材料参数量化模型与实际结构系统材料参数不确定性之间存在偏差,包括模型本身由于初始样本数量不足以及未能考虑密度等其他参数引起的不确定性等方面的误差;② 各测点处的实测响应样本不足,响应方差统计结果本身存在误差.在上述误差来源的影响下,基于不确定性材料参数量化模型计算得到的各测点处动响应的统计特征与实测动响应样本统计结果必然会存在一定偏差,对不确定性材料参数量化模型精度的验证也会带来干扰.然而,图11中的结果对比仍然可以一定程度反映本研究提出的不确定性材料参数量化模型的准确性.

图12 振动试验系统
5 结论
1) 本文针对纤维编织复合材料等效宏观力学性能的离散性,开展了基于小样本试验数据的复合材料梁弹性模量不确定性量化方法研究.
2) 采用谱分解方法建立不确定性材料参数量化模型,将不确定性问题转化为确定性问题,降低了问题求解的难度;结合了实测样本的先验信息,采用贝叶斯理论建立不确定性材料参数量化模型,在小样本试验数据情况下,能够准确反映含不确定性复合材料参数的统计特征;同一批次同工况下的复合材料梁振动试验验证了不确定性量化方法的可行性.
3) 所提出的方法能够充分考虑结构系统因复合材料力学性能离散而导致的随机不确定性和因数据缺乏或信息不完善而产生的认知不确定性,解决了传统概率分析模型需要大样本数据的缺陷;同时,基于谱分解不确定性参数量化模型的维度与结构模型的单元数量无关,对工程中的复杂结构具有较好的适应性.
4) 本方法目前仍然针对的是相对独立的系统参数,对复合材料结构中存在多个相关的不确定性参数工况,还需要进一步研究.

