基于稀疏度区间的变步长最优子空间追踪算法
孙润润
(安徽理工大学 计算机科学与工程学院,安徽 淮南 232001)
1 概 述
传统的信号采样技术通常基于Nyquist采样定理:只有当采样频率大于信号带宽的2倍以上时,采样后的数字信号才能得到原有完整的信息。高采样频率使得采样的数据量过大导致资源浪费,给硬件系统、存储处理和成本带来很大的压力。近年来国际上出现的压缩感知理论(compressed sensing,CS)解决了一系列问题。该理论指出:如果信号是稀疏的或者在某一个稀疏域是稀疏的,那么可以选取与稀疏基不相关的矩阵对信号进行低维投影,再通过一系列的L1范数最小化的优化算法进行重建,可以较高精度地重构出该信号[1]。
因此,压缩感知理论打破了传统采样定理的先压缩再采样的模式,使用采样压缩并用的技术极大地节省了资源,而且目前该理论已涉及众多领域,具有极大的应用价值和研究前景。
压缩感知理论主要包括三个方面:稀疏、低维观测和重构。在现实生活中很少有信号是真正稀疏的,当某个信号是可压缩时,代表该信号是可以通过稀疏信号来近似表达的。假设采样信号X(X∈RN×1),稀疏基Ψ(Ψ∈RN×N)为正交矩阵,则X可以表示成:X=ΨΘ,即为信号X在稀疏域的稀疏表示。其中Θ的非零元个数为K(K≪N),则信号X是K-稀疏的。其中常用的稀疏基包括傅里叶变换基、离散余弦基。
信号X经过稀疏基变换成稀疏信号后,再通过选取与稀疏基不相关的矩阵对信号进行压缩。假设选取矩阵Φ(Φ∈RM×N)为观测矩阵,对信号进行低维观测:Y=ΦΨΘ=ΦX,其中传感矩阵A=ΦΨ,满足M≥Klog(N/K)。其中观测数Y的维数M远小于信号X的维数N,即K 对于上述公式的求解主要分为凸优化类算法、组合算法和贪婪算法。凸优化算法是将非凸问题转化成凸问题进行求解,计算复杂度高,包括BP算法、内点法、梯度投影法和迭代阈值法。组合算法要求信号的采样支持分组测试而快速重建,但是应用不大,包括傅里叶采样、链式追踪和HHS(heavg hitters steroids)追踪。贪婪类算法在每次迭代中寻找一个局部最优解来逐步逼近原始信号,运算速度快且重构效果好,与其他两种方法相比应用广泛。 贪婪类算法的典型首先是匹配追踪算法MP(matching pursuit)[2],算法相对简单但是不能保证重建误差足够小,并且每次迭代的结果不是最优而是次优的。为解决这些问题,随后出现了正交匹配追踪算法OMP(orthogonal matching pursuit)在正交方向寻找非零元,保证了迭代的最优性,减少了迭代次数[3]。为了提高算法的收敛速度,随后发展起来的算法有分段匹配追踪算法StOMP(stagewise OMP)[4]、正则化正交匹配算法ROMP(regularized orthogonal matching pursuit)[5]。后来又引入了具有回溯思想的压缩感知匹配追踪算法CoSaMP(compressive sampling matching pursuit)、子空间追踪算法SP(subspace pursuit)[6]。以上这些算法都是基于稀疏度为先验知识,但是现实生活中稀疏度K通常是未知的。T.DO等提出了稀疏度自适应匹配追踪算法SAMP(sparse adaptive matching pursuit)[7],在迭代过程中逐渐改变步长,使得逐渐逼近稀疏度K。逐步最优子空间追踪算法SOSP(stepwise optimal subspace pursuit)是一种使用逐个最优扩增缩减方法修正假定支撑集的算法,保证了残差的收敛性且重构精度较高[8-9]。 文中提出的基于稀疏度区间的变步长最优子空间追踪算法VssOSP(Variable step size optimal subspace pursuit algorithm based on sparsity interval)就是在SOSP的最优增减支撑集的基础上,打破稀疏度自知的限制,根据匹配测试公式获取初始固定步长。再在假定支撑集的增加过程中,根据信号残差能量的迭代变化先判断稀疏度的区间。随着支撑集个数的不断增加,残差内积将首先单调减小最后保持为一个很小的值,且稳定在较小的范围内[10-13]。再在稀疏度区间中使用黄金分割法逐渐得出信号稀疏度,并在区间分割的过程中逐渐删减假定支撑集中多余的元素,最终重构原始稀疏信号。 公式一:分块矩阵求逆。 由上式可以看出含有公因式(D-CA-1B)-1,令f=D-CA-1B,则原式化简为: 公式三:假定支撑集增加过程中残差变化ΔS的迭代公式。 公式四:删减假定支撑集元素的迭代公式,i∈S。 公式五:假定支撑集删减过程中残差变化ΔS的迭代公式。 文中提出的基于稀疏度区间的变步长最优子空间追踪算法在K未知的条件下,首先使用匹配测试的方法获得初始的固定步长值,此步长接近且小于K值,并获得初始支撑集。再选择残差内积增量最大的原子加入支撑集,直到满足条件停止增加并获得稀疏值K的估计区间。由于支撑集个数逐渐增加时,残差内积首先会迅速下降,然后趋于稳定的状态,残差变化的拐点区间就是K值区间。当支撑集原子个数L≥K时,K个稀疏系数都会被选中。随着残差能量单调递减,最终收敛在一个局部最小点。最后确定残差变化过程的拐点位置,即稀疏估计。通过区间的减小同时实现支撑集多余元素的删减,最终重构信号。算法分为以下三个步骤: 步骤一:选取初始固定步长。 步骤二:增加支撑集直到达到要求,获得稀疏度K的区间和增加后的支撑集。 根据步骤一得到的K0,定义步长L=K0,步长增量step=K0,t为迭代次数,Rk为第k次的标记,k为标记次数,阈值ε。 (1)以L为步长首先增加支撑集,根据公式二、三选择残差内积变化量最大的前L个元素,依次加入支撑集。 (2)根据增加过程中的残差变化量进行判断,若当前残差内积Δnew小于上一次迭代的残差内积Δt-1,则Δt=Δnew,t=t+1,L=L+step,继续增加支撑集,返回步骤(1)。 (3)若当前残差内积Δnew大于或等于上一次迭代的Δt-1,说明残差内积开始变大或者基本不变,则可能此时L≥K。此时开始标记上一次的残差内积:Rk=rt-1,k为标记次数。 (4)若此时连续两次标记的位置上的残差内积之间的差值大于等于阈值ε,即Rk-1-Rk≥ε,则L=L+step且返回继续增加支撑集,返回步骤(1)。 (5)若此时连续两次标记的位置上的残差内积之间的差值小于阈值ε,即Rk-1-Rk<ε,则停止迭代增加支撑集,稀疏度区间则为[L-2step,L-step]。 步骤三:黄金分割稀疏度区间至得到K值,同时剔除多余支撑集元素,重构稀疏信号。 根据步骤二得出的区间,定义区间最大值为Lhigh,区间最小值为Llow,区间长度range=Lhigh-Llow,取估计稀疏值Ktry=Ltry=Lhigh-range*0.382。支撑集剔除残差变化量最小的L个元素,其中L采用黄金分割法(golden ratio)从区间中获取。 (1)根据公式四、五剔除支撑集S前Lhigh-Llow个最小残差变化量,得到当前假定支撑集St。 (2)若此时两次的残差变化小于阈值ε,即Δtry-Δhigh<ε,则S=St,Lhigh=Ltry,保留删除后的支撑集,返回步骤(1)。 (3)此时两次残差变化大于或等于阈值ε,Llow=Ltry不保留删除后的St,Ltry=Lhigh-range*0.382,返回步骤(1)。 (4)不断缩小K值范围直到最终确定K值和相应的支撑集以及残差。 为了验证文中提出算法的重建效果和性能,对算法进行了一系列的仿真验证实验。在实验中,M=128,N=256,观测矩阵为M×N阶独立分布高斯随机矩阵,原始信号x为K稀疏的矩阵(从x中随机选取了K个位置,其中每个位置为独立分布的高斯随机变量,其他项为零),稀疏基为单位矩阵,通过y=Φx得到观测矩阵y。首先将文中算法VssOSP和典型的贪婪算法OMP、ROMP、SP、SAMP、SOSP进行一系列的性能仿真实验对比,如图1所示。 从图1(a)可以看出,所有重构算法在M固定且稀疏度K不断增大的情况下准确重建率不断减小。但各类算法精确重构所适用的信号稀疏度范围有显著差别,OMP、ROMP、SAMP、SP、SOSP、VssOSP在K≤18,K≤35,K≤46,K≤37,K≤48,K≤50时能够保证100%准确重构稀疏信号;在50≤K≤62时,VssOSP的重建概率开始明显下降,但依然高于OMP、ROMP、SP、SOSP,稍低于SAMP;但是在62≤K≤70时,VssOSP开始稍高于SAMP、SOSP。相对来说,在在信号所需采样数M一定的情况下,VssOSP算法能稳定重建稀疏度更高的信号。 (a)不同稀疏度K时的重建率(M=128,N=256) (b)不同测量值M时的重建率(K=20,N=256) 从图1(b)同样可以看出,各重构算法在稀疏度固定且采样数越大时准确重构率越大。但ROMP、SP、SAMP、SOSP、VssOSP在M≥92,M≥90,M≥80,M≥85,M≥80时准确重建概率接近为1;在M≥53时,VssOSP算法准确重构率明显超过OMP、ROMP、SP、SOSP,稍高于SAMP。总体来说,VssOSP算法能稳定重建信号,所需的采样数较少。 为检验VssOSP算法对二维图像信号的重构性能,选择标准的二维灰度图像(256×256的Lena图片)进行重构,通过比较不同算法的峰值性噪比来判断不同算法的性能。为提高重构信号的质量,先采用离散余弦变换进行基稀疏变换,然后将变换后的各行作为一维信号进行压缩采样,再用不同算法进行重建,重建完成之后再通过反变换得到重建图像。其中观测矩阵Φ为高斯随机矩阵,稀疏基Ψ为单位阵。 定义图像的采样率为M/N。重建图像的质量用峰值性噪比(peak signal to noise ratio,PSNR)表示。运行时间以秒为单位,PSNR以dB为单位。不同算法重构Lena的效果图如图2所示。可以看出,VssOSP算法的重构效果明显优于SP、CoSAMP算法,稍优于ROMP、OMP、SAMP、SOSP算法。经VssOSP算法重建后的图像与原始图像相近且有良好的视觉效果。 图2 不同算法重构Lena的效果 表1给出了各种算法在不同压缩比M/N为0.3、0.4、0.5时重建图像的PSNR和运行时间的对比。可以看出,随着采样率的增大,各种重建算法重建图像的PSNR均显著增大,通过增加观测数目可以提高重建图像的重建质量;在相同压缩比的条件下,VssOSP算法重建图像的PSNR值均为最大,说明该算法对图像的重建精度较高。 表1 不同采样率下重构算法的性能对比 另外,根据表1中的时间数据可以看出,随着采样数的增大,各种重建算法运行时间均增大,而VssOSP的运行时间明显高于其他非稀疏自适应算法。从结果看,VssOSP运行时间稍高于SOSP,低于SAMP。 提出的VssOSP算法是在SOSP算法最优扩增缩减方法理论基础上,打破稀疏度自知的限制,首先使用匹配测试的方法获得初始的固定步长值,此步长接近且小于K值,并获得初始支撑集。再选择残差内积增量最大的元素加入支撑集,直到满足条件停止增加并获得稀疏值K的估计区间。由于支撑集个数逐渐增加时,残差内积首先会迅速下降,然后趋于稳定的状态,残差变化的拐点区间就是K值区间。最后确定残差变化过程的拐点位置,即稀疏估计,通过区间的减小同时实现支撑集多余元素的删减,最终重构信号。 实验结果表明,在各种算法性能对比之下,VssOSP在稀疏度递增或采样数变化时都可以很好地重建原始信号,重建时间稍高于SOSP,低于SAMP,且重建后的图像与原始图像相近且有很好的视觉效果。2 基于稀疏度区间的变步长最优子空间追踪算法
2.1 符号定义与理论推导
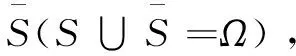
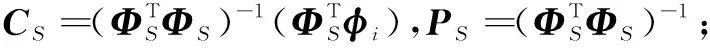
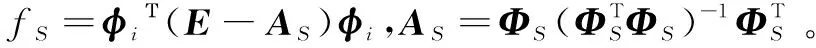
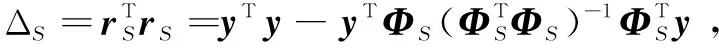
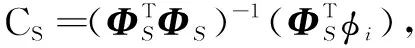
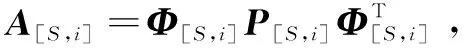
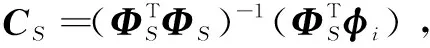
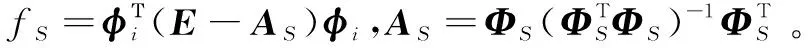


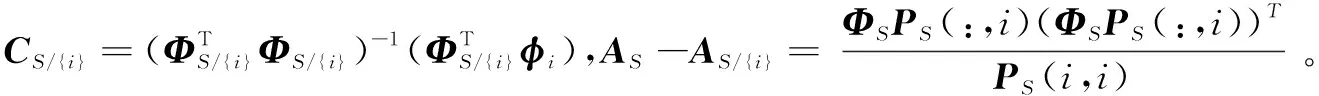
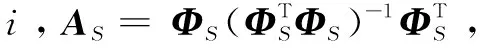
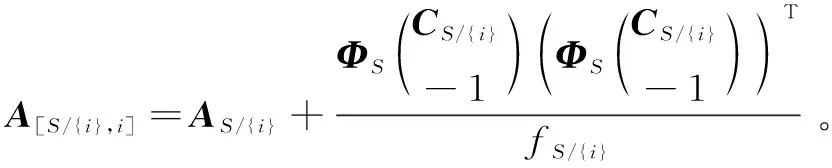
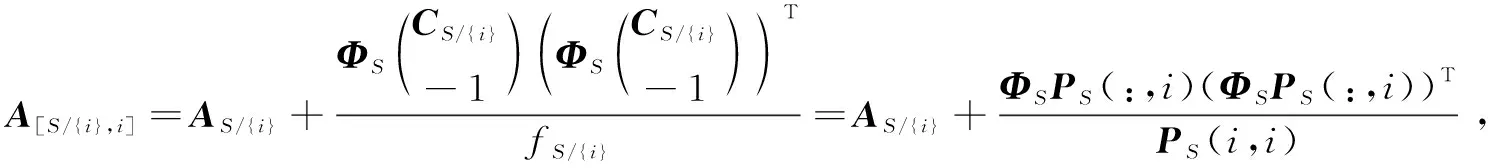
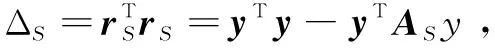
2.2 算法步骤
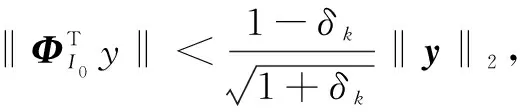
3 仿真实验结果及分析
3.1 信号重建性实验
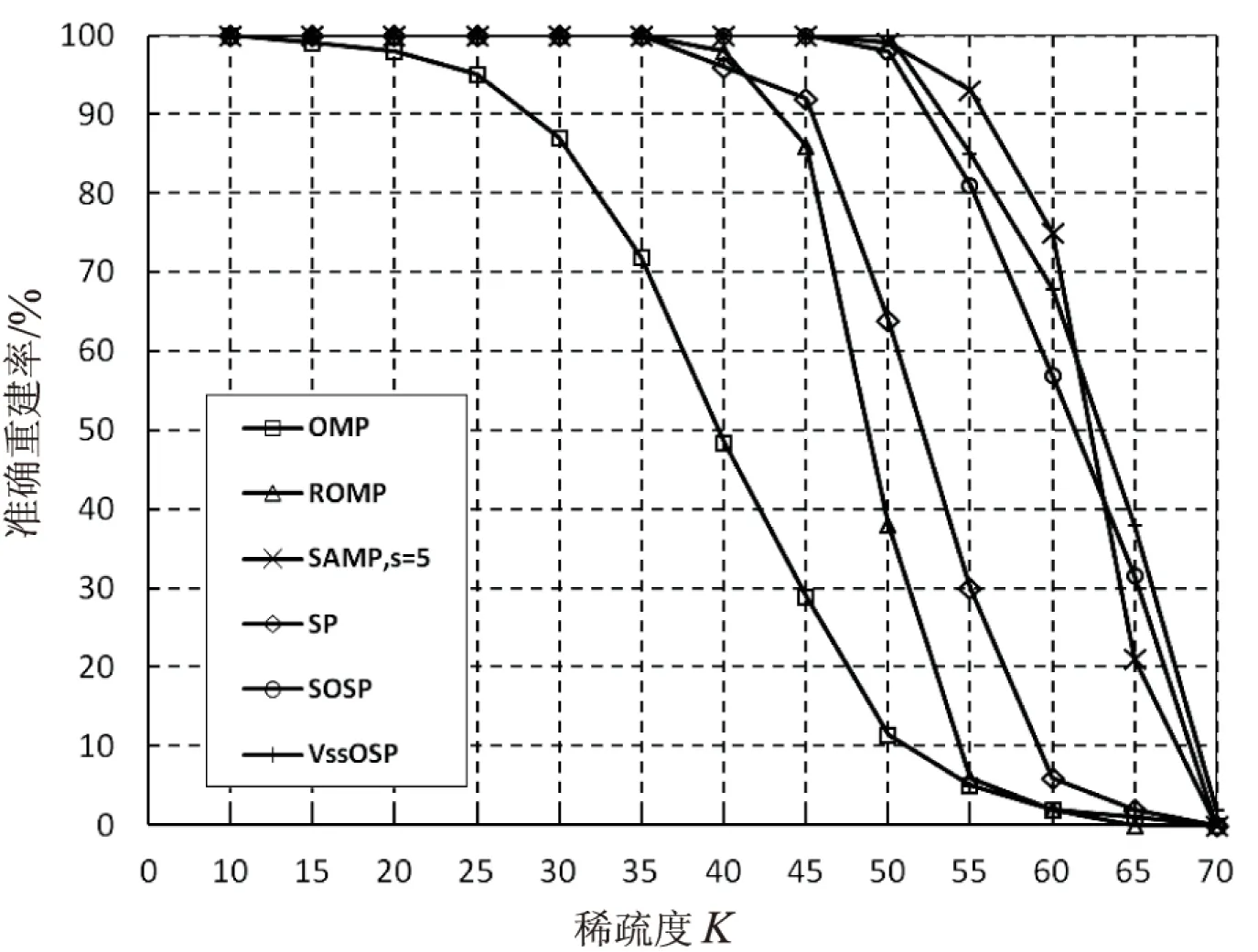
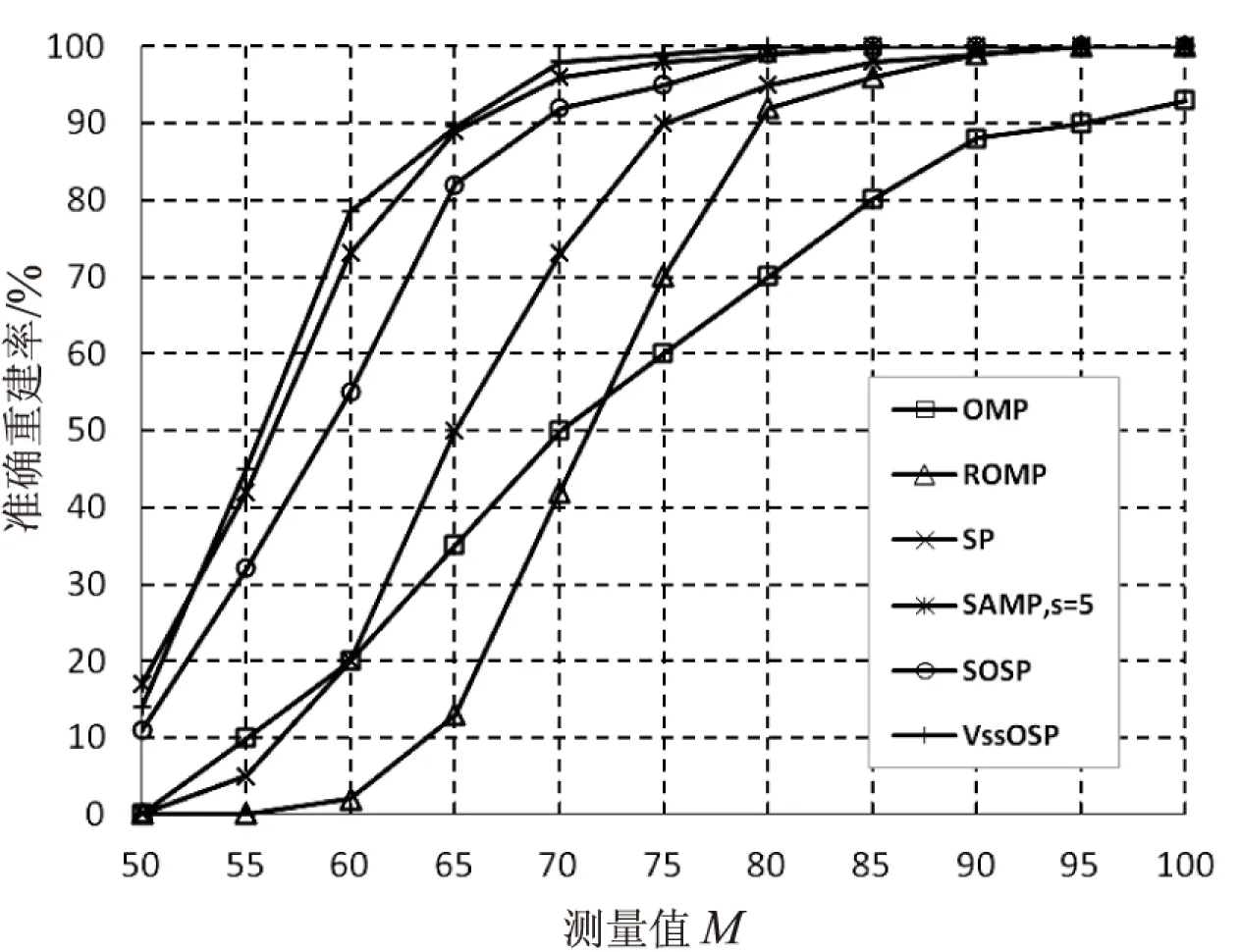
3.2 图像重建实验


4 结束语

