基于符号计算的变系数KP方程的孤子解

薛瑞梅，王书敏，姚若侠

(陕西师范大学 计算机科学学院，陕西 西安 710119)

0 引 言

计算机科学的蓬勃发展推动了其他学科的发展，计算机符号计算系统[1-3]的出现为人类分析和研究数学物理模型提供了极大的便利。近年来，计算机科学在数学物理领域的应用，使得非线性科学焕发了新的活力。在力学、物理学、生命科学、工程技术等许多领域，非线性偏微分方程的精确解都发挥着重要作用。科学研究者提出了大量的求解非线性微分方程的方法，如反散射法[4]、双线性法[5]、齐次平衡法[6]等。而变系数非线性偏微分方程往往比常系数的非线性偏微分方程具有更广泛的物理意义，它的解更具一般性，也更贴近现象的本质。Maple作为一个应用广泛的符号计算系统，结合了世界上最强大的数学引擎和接口，使用它非常容易分析、探索、可视化和解决数学问题。1970年，Kadomtsev和Petviashvili提出的用以描述散色和非线性介质中的扰动KP方程[7]，在流体力学、气体动力学等领域有着广泛的意义，它的解对许多问题都有重要的参考价值[8]。文中借助计算机符号计算系统Maple，通过修正的CK直接约化方法[9-11]和推广的Painlevé非标准截断方法[12-14]求解一类变系数KP方程。

文中研究的一般变系数KP方程的形式如下[15]：

[ut+f(t)(6uux+uxxx)]x+g(t)uyy=0

(1)

其中，f(t),g(t)是关于t的任意函数。当f(t)=a,g(t)=b(a,b是常数)时，式1变为常系数方程。

[ut+a(6uux+uxxx)]x+buyy=0

(2)

以Maple为计算工具，采用修正的CK方法获得了式1与式2的解之间的关系，再利用Painlevé非标准截断方法构造出式2的解，继而获得式1的解。

1 变系数KP方程的CK约化

设式1有如下形式的解：

u(x,y,t)=α(x,y,t)+β(x,y,t)U(X,Y,T)

(3)

其中，α=α(x,y,t),β=β(x,y,t),X=X(x,y,t),Y=Y(x,y,t),T=T(x,y,t)均为待定函数，并且在变换{u,x,y,t}→{U,X,Y,T}下，要求U(X,Y,T)满足式2，即

(UT+a(UUX+UXXX))X+bUUYY=0

(4)

其中，a,b是常数。

式1的约化过程如下所述：

(1)调用Maple的偏微分方程工具包PDEtools，即[>with PDEtools()；然后在Maple中输入式1；

(2)调用微分替换函数dsubs()，执行dsubs()语句，用式3替换式1中的u之后，再将式4代入；

(3)借助collect()函数和coeff()函数，整理并提取出未知函数U及其导数项系数，令其为零，由此可获得一个代数方程组，解之得：

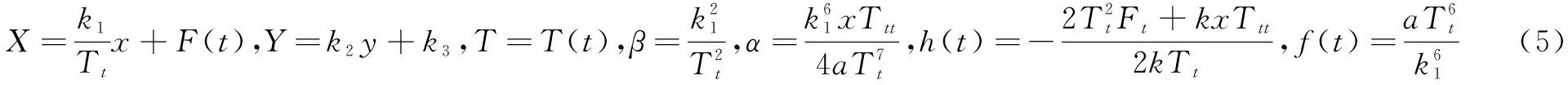
其中，F(t),T(t)是t的任意函数；k1,k2,k3是任意常数。

在Maple中式1约化过程的主要算法如下：

>restart:with PDEtools();

>PDEque:=方程(1);#将方程(1)输入计算机，命名为“PDEque”

>equ1:=dsubs(u(x,y,t)=α(x,y,t)+β(x,y,t)U(X,Y,T),PDEqu);

>equ2:=equ1-(UT+α(UUx+UXXX))X+bUUYY=0;

>equ3:=collect(equ2，U(X,Y,T));

#以下部分提取出未知函数U及其导数项系数，由此可获得一个代数方程组，解之

>str:=[]:

>for i from 1 tonops(equ3) do

>ss(i):=coeffs(op(i,equ3),U(X,Y,T)):

>str:=[ss(i),op(equ3)]:

>od:

>str;

>solve(str);

根据上述过程，有如下定理：

定理1：如果X,Y,T,α,β按式5给出，则式1的解可表示为：

(6)

2 常系数KP方程的Painlevé非标准截断展开

通常，对于如下给定的偏微分方程：

F(t,x1,x2,…,xn,u,ux1,ux2,…,uxi,

ux1x1,…,uxixj…)≡F(u)=0

(7)

它的Painlevé展开为：

(8)

其中，φ≡φ(x1,x2,…,xn,t)=0是任意的奇性流形，由于φ的任意性，Conte[16]令：

(9)

即可获得一个新的展开式：

(10)

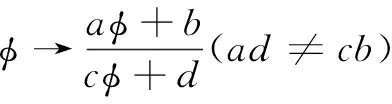
对于2+1维系统(y=x2),将式9分别对x,y和t求微分，可得下述三个恒等式：

(11)

其中

(12)

其中，S,C,K均在Mobious变换下保持不变。

Pickering对上述方法作了进一步推广[17]，取一个新的变量g作为一个新的展开函数使得展开式为：

(13)

其中，g要满足以下条件：

(14)

式14的自洽条件为gxt=gtx,gyt=gty,gxy=gyx。

所要研究的(2+1)维KP方程具有以下形式：

[ut+a(uux+uxxx)]x+buyy=0

(15)

将u按照Pickering推广的方法展开为：

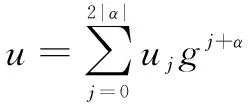
(16)

借助主项平衡，得到α=-2，代入式16，展开如下：

(17)

其中g要满足式14。

继而，与第二部分约化过程一致，这里就不再对算法进行赘述。借助Maple系统的dsubs()函数，把式14和式17代入式15；再用collect(equation，g)语句整理方程；然后，再把所得到的方程通过Maple系统的sort()函数，按照g的幂次高低排列；最后，提取g的各个幂次项的系数。如果仅仅希望得到原方程的孤子解的话，则可以令S=s,C=c,K=k，也就是说把它们当作常数处理，此时再令g的各次项系数为零，即可得到一系列复杂的方程组，通过Maple计算，在之后给出结果，式中的s,c,k均为常数，且由式14通过Maple计算可得：

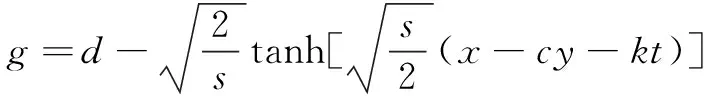
(18)

参数解1：

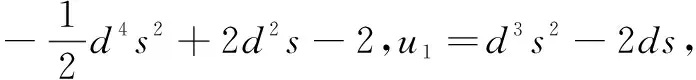
u3=0,u4=0

(19)

对应式2的单孤子解为：

(20)

当s=1,c=1,k=0,a=1,b=1,d=1(或者s=1,c=0,k=1,a=1,b=1,d=1)时，用Maple中的Plots命令可以轻易画出解的三维图，如图1所示。

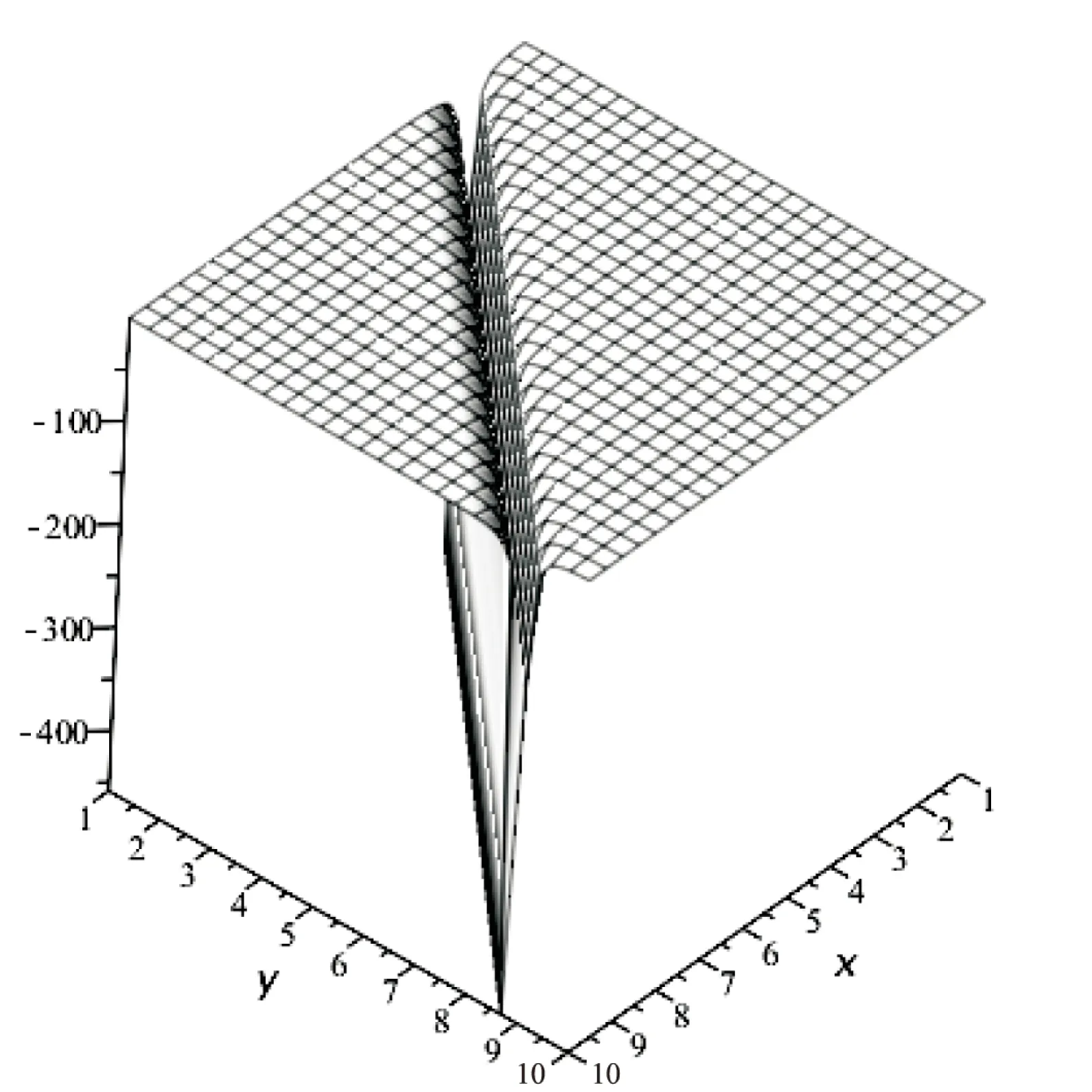
图1 三维图(1)

参数解2：

(21)

对应式2的单孤子解为：

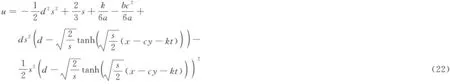
同样，当s=1,c=0,k=1,a=1,b=1,d=1(或者s=1,c=1,k=0,a=1,b=1,d=1)时，解的三维图如图2所示。

利用式6进而得到式1的单孤子解。

解1：

(23)

解2：

(24)

通过对变系数KP方程的求解，可以发现：利用Maple只需很少的执行语句，就可以轻松地对复杂的变系数KP方程求精确解，并且可以利用Maple中的Plots命令绘制约化后的常系数方程孤子解三维的图形，使数学问题可视化，有助于研究者直观地分析微分方程的解。

3 结束语

以符号计算系统Maple为工作平台对变系数KP方程进行求解，利用修正的CK直接约化方法建立了变系数KP方程与其对应的常系数方程之间的关系，之后利用推广的Painlevé非标准截断展开法分析了常系数方程，求出了常系数方程的两个解，进而得到变系数KP方程的两个单孤子解。实验结果表明，该方法可用于一部分变系数偏微分方程的求解。