关注方法本质 提高运算能力*
——基于解析几何复习的思考与解题策略透视
●
(杭州高级中学,浙江 杭州 310003)
解析几何是考查学生数学思维能力与数学运算能力的重要内容之一,也是高考一直来重点考查的内容,这一内容在高考中有着很好的区分度.解决解析几何问题,需要将代数方法与几何图形完美结合.在此过程中,无论使用哪一种方法,都面临两个问题:一是方法中蕴含的数学思想;二是运算中体现的技巧能力.对这两者的认识不足,是绝大多数学生解题半途而废的根源.因此,对解析几何问题的思路分析、运算技巧等方面的研究有着重要的意义.如何更好地掌握这一部分知识,更有效地解决这一类问题,值得去探索、去研究.以下就此谈谈解析几何问题的思考与解决策略.
1 注重概念落实,重视定义特征
许多圆锥曲线问题都具有比较典型的几何特征,因此我们常说解析几何首先是几何问题,特别是圆锥曲线的定义,体现了圆锥曲线的本质.对一些具有典型定义特征的解析几何问题,毫无疑问地可以联想到定义的应用,通过定义及相应的知识解决问题.这对加快解题速度、提高解题正确率无疑是一种重要的解题策略.
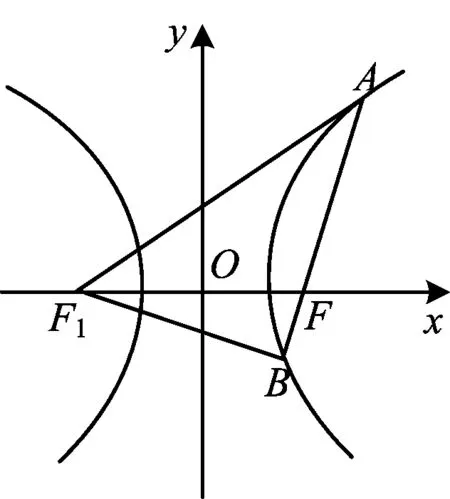
图1
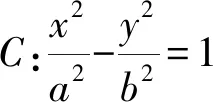
( )

解设双曲线的左焦点为F1,|BF|=t,则
|AF|=4t,
由定义得 |AF1|=2a+4t, |BF1|=2a+t.
在△AF1F和△BF1F中,根据余弦定理得
即
两式相减得
12at=10ct,
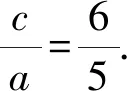

( )
(2010年全国数学高考卷Ⅱ理科试题第12题)
思路分析该题与例1虽然一个是双曲线、一个是椭圆,但同属圆锥曲线且题型结构类似,设左焦点F1并联结AF1和BF1,结合定义与余弦定理,同样可顺利解决.答案为B.
评注该方法紧扣定义,思路简捷,只需根据题意构造焦点三角形.该方法对于解决这类问题有一定的通用性.
2 抓住题型结构,重视运算过程
正确的解题思路不一定就能得到问题的正确结果,思路正确仅仅是解题的一个方面,运算能力与运算技巧等综合能力才是优秀学生需要具备的.培养运算能力、掌握一定的运算技巧对解决解析几何问题尤其重要,加强运算训练、提升运算能力、掌握运算技巧也是解决这类问题的重要策略[1].

图2
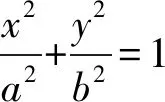
1)求椭圆的离心率;
2)已知a=2,四边形ABCD内接于椭圆,AB∥DC,记直线AD,BC的斜率为k1,k2,求证:k1k2为定值.
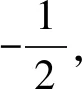
由题意得椭圆方程为
因为AB∥DC,所以
从而直线CD的方程为
与椭圆方程联立得
x2-2mx+2m2-2=0,
从而
x1+x2=2m,x1x2=2m2-2,
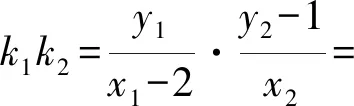
算到这里,许多学生运算受阻,发现韦达定理只能代入一部分,无法继续算下去.其实我们可以这样思考,首先题目中要证明的是定值,那么最后结果肯定是定值,可以先把能代入的先代入,进一步进行化简,根据化简后的式子进行分析即可.由韦达定理得
为了证明它是定值,只要把分子、分母往同一个方向化简即可,分子用x1=2m-x2代入可得
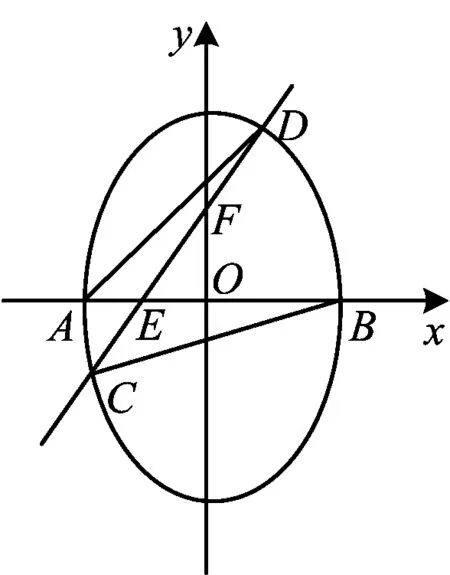
图3


2)设直线AD,CD的斜率分别为k1,k2,若k1∶k2=2∶1,求k的值.
思路分析第2)小题中直接写出k1,k2,并代入k1∶k2=2∶1可得.思路简单明了,但具体运算同样需要运算能力来保证.具体如下:
设C(x1,y2),D(x2,y2),则
代入k1∶k2=2∶1,得
(1)
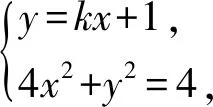
(4+k2)x2+2kx-3=0,
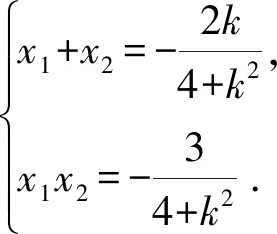
算到这里,不少学生无法继续下去,原因是式(1)无法使用韦达定理.如果换个角度,想办法代入椭圆方程,就可以使问题迎刃而解.
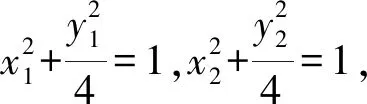
(2)
式(1)两边平方得
把式(2)代入得
即
3x1x2+5(x1+x2)+3=0.
利用韦达定理可得
3k2-10k+3=0,

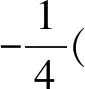
从而
即
8kBDk2=-1.
又
于是
利用韦达定理可求出k=3,不需要检验.
另外,在解析几何问题的解决中,还可以用特殊位置来验证结果的正确性,比如例3中直线CD过原点时可很快验证结果的正确性,确保万无一失.
3 把握全局观念,重视横向联系
椭圆、双曲线与抛物线统称圆锥曲线,它们之间有着许多关系及共同的性质,这对学习解析几何有着重要的意义.如对抛物线y2=2px(其中p>0),过原点O的两条互相垂直的直线OA和OB交抛物线于点A,B,则直线AB必过定点(2p,0).这个性质可以推广到过抛物线上任意一点的性质:
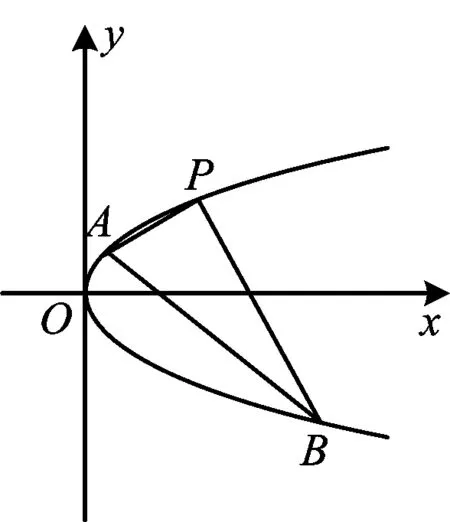
图4
例5如图4,已知P(x0,y0)是抛物线y2=2px(其中p>0)上一定点,过点P作两条互相垂直的直线PA,PB,交抛物线于点A,B,求证:直线AB过定点,并求这个定点.
分析如果设PA,PB的直线方程,虽然可以求出点A,B的坐标,但运算会比较复杂.如果用设点法解决,就会比较简单.
解设A(x1,y1),B(x2,x2),可得
又PA⊥PB,得
即
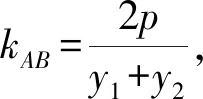
即
所以 (y1+y2)y= 2px+y1y2=
即 (y1+y2)(y+y0)= 2px-4p2-2px0=
2p(x-2p-x0),
故直线过定点(2p+x0,-y0).
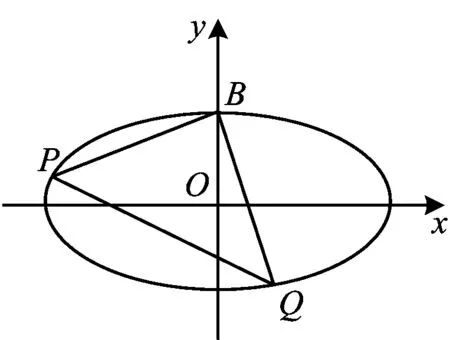
图5
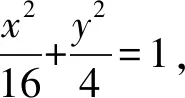
思路分析该题是过椭圆上一点B的两条相互垂直的直线与该椭圆相交的问题,可以求出点B,Q的坐标,运算过程可预见到联立方程后必定是一个不带常数项的二次方程,计算相对比较容易.也可以设直线PQ的方程,然后代入kBPkBQ=-1中.
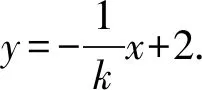
(1+4k2)x2+16kx=0,
解得
从而
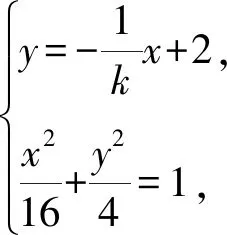
则
故直线PQ的方程为
即

另一种方法就是:设直线PQ的方程为y=kx+m,联立椭圆方程,运用韦达定理,然后由BP⊥BQ,得
可以得到m与k的关系,从而得证.
评注解析几何中,有各种同类的题组,很多性质是一系列的.在一种圆锥曲线中所具有的性质,往往在另一种圆锥曲线中也会有类似的结论,注意知识之间的横向联系,并进行纵向深化,这对形成知识体系有一定的帮助.
4 培养良好习惯,重视思想方法
解析几何主要研究两大问题,那就是曲线与方程问题,探究几何特征、注重方程思想是研究这类问题的主要内容.方程思想在浙江省数学高考中也多次用到,题意分析中蕴含思想方法,具体运算中体现数学能力.

图6
例7如图6,已知点P是y轴左侧(不含y轴)一点,抛物线C:y2=4x上存在不同的两个点A,B满足PA,PB的中点均在C上.
1)设AB中点为M,证明:PM⊥y轴;

(2018年浙江省数学高考试题第21题)
分析第1)小题中,由于PA,PB具有相同的性质,因此可以用方程的思想来解决,即两个方程同一个形式,可以合二为一.第2)小题中,把|PM|,|AB|转化为关于y1,y2的代数式,再运用韦达定理,思维方向明确,但需要一定的运算能力才能完美解决问题[3].
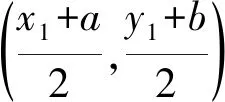
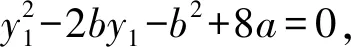
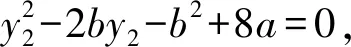
于是y1,y2是方程y2-2by-b2+8a=0的两个根,可得

2)解△PAB的面积为
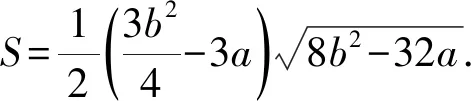
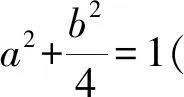

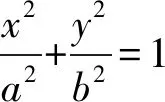
分析两条切线方程具有相同的形式,可以利用方程思想解决.

由于两条切线均过点M(xM,yM),于是
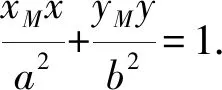
评注这类问题既蕴含了数学思想,又体现了运算能力.只有全面分析、确定方法、熟练运算,才能得到正确的结果.
解析几何是高考的重点内容,同时也是学习的难点.有人认为是方法难找,也有人认为是运算太烦,笔者认为主要难点恰恰是两者的统一,思维分析给运算提供了方法,也给运算者增强了信心,而运算能力使正确的思维方法得到实现.只有两者完美组合,才能使解析几何问题得到真正解决.

