“ 圆 ”源不断

吴晓刚

在每年的中考数学大戏里，圆都是重头戏。有关圆的中考试题很多来源于教材，下面，我们撷取两例，以帮助同学们固本清源。

【原题再现】苏科版九（上）57页例2：

如图1，AB是⊙O的直径，弦CD交AB于点E，∠ACD=60°，∠ADC=50°，求∠CEB的度数。

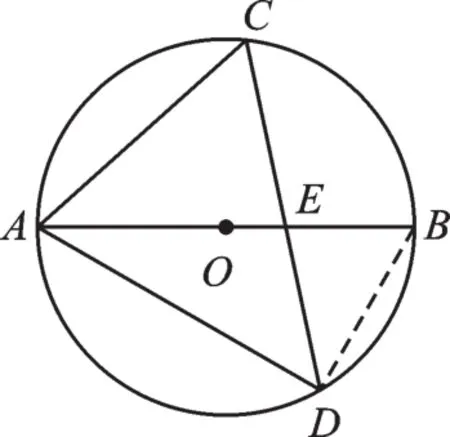
图1

【解析】连接DB。AB是⊙O的直径，根据“直径所对的圆周角是直角”，可得∠ADB=90°，再 由 ∠ADC=50°可 得 ∠CDB=40°。 ∠ACD，∠ABD都是︵AD所对的圆周角，根据“同弧所对的圆周角相等”，可得∠ACD=∠ABD=60°，最后利用外角性质，可得∠CEB=∠ABD+∠EDB=60°+40°=100°。

【点评】本题意图是让同学们掌握圆周角定理，学会通过构造直径所对的圆周角来解决圆中的角度问题。一条弦所对的弧有两条，本题还可以利用另一个半圆上的点C，连接BC，构造直角∠ACB来解决。

变式1 如图2，AD为△ABC的外接圆⊙O的直径，若∠BAD=50°，则∠ACB= 。

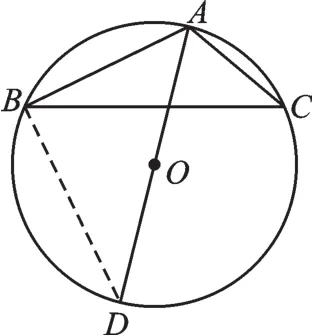
图2

【解析】连接BD。由AD为△ABC的外接圆⊙O的直径可得∠ABD=90°，若∠BAD=50°，则∠D=90°-∠BAD=90°-50°=40°，所以∠ACB=∠D=40°。

【点评】本题是教材例题的翻版，只是对图形结构进行了异化，单纯考查圆周角的知识，突出了“遇到直径，构造直角”的转化方法。

变式2 如图3，AC为⊙O的直径，点B在圆上，OD⊥AC交⊙O于点D，连接BD，∠BDO=15°，则∠ACB= 。

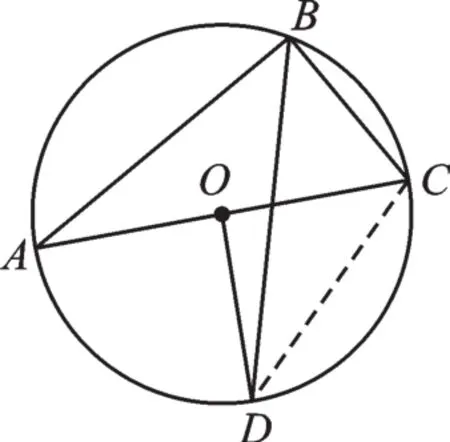
图3

【解析】连接DC。由OD⊥AC，OD=OC，可得∠ODC=45°，又∠BDO=15°，则∠BDC=30°。根据“同弧所对的圆周角相等”，可得∠A=∠BDC=30°。由AC为⊙O的直径可得∠ABC=90°，并由此求得∠ACB=60°。

【点评】本题的突破口是由“OD⊥AC”构造出一个等腰直角三角形。如果连接AD，再利用弧AB转化圆周角，亦可构造求解。

【原题呈现】苏科版九（上）93页第16题：

如图4，在△ABC中，∠C=90°，⊙O是△ABC的内切圆，切点分别为D、E、F。若BD=6，AD=4，求⊙O的半径r。

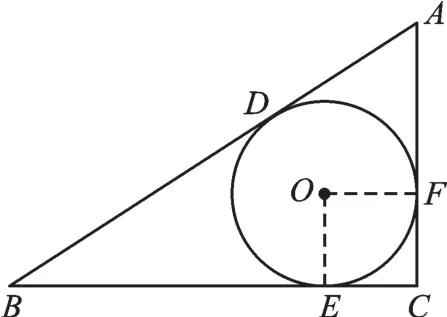
图4

【解析】连接OE、OF，可得四边形OECF是正方形，设OE=OF=CE=CF=r。由切线长定理可得 BD=BE=6，AD=AF=4，则 BC=6+r，AC=4+r，再根据勾股定理，可得（6+r）2+（4+r）2=102，整理得r2+10r-24=0，解得r=2或-12（不合题意，舍去）。

【点评】本题是教材中的一个习题，图形的基本框架是直角三角形内切圆，主要考查了切线长定理。解题的关键是在直角三角形中，以内心、直角顶点、两直角边的切点为顶点构造正方形这个基本图形，再运用勾股定理、方程思想即可求解。

变式1 在Rt△ABC中，∠C=90°，CA=8，CB=6，则△ABC内切圆的周长为 。

图5

【解析】在Rt△ABC中，∠C=90°，CA=8，CB=6，则AB=10。如图5，连接OE、OF，可得四边形OECF是正方形。设OE=OF=CE=CF=r，则AD=AE=8-r，BD=BF=6-r，列方程，得（8-r）+（6-r）=10，解得r=2，则△ABC内切圆的周长为4π。

【点评】本题的主体还是直角三角形内切圆，图形结构与教材原题无异，只是计算与方程的建立是原题的逆向应用。数学基础好的同学可以直接利用直角三角形内切圆半径公式（S是△ABC的面积，a、b为直角边，c为斜边）得到答案。

变式2 结果如此巧合！下面是小颖对一道题目的解。

题目 如图6，Rt△ABC的内切圆与斜边AB相切于点D，AD=3，BD=4，求△ABC的面积。

图6

解：设△ABC的内切圆分别与AC、BC相切于点E、F，CE的长为x。

根据切线长定理，得AE=AD=3，BF=BD=4，CF=CE=x。

根据勾股定理，得（x+3）2+（x+4）2=（3+4）2。

整理，得x2+7x=12.=12

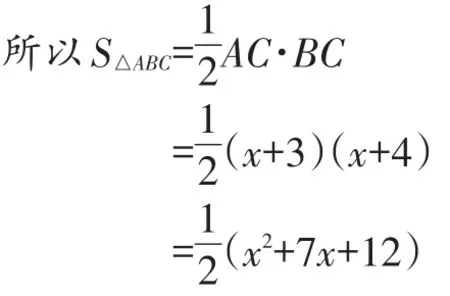
小颖发现12恰好就是3×4，即△ABC的面积等于AD与BD的积。这仅仅是巧合吗？

请你帮她完成下面的探索。

已知：△ABC的内切圆与AB相切于点D，AD=m，BD=n。

可以一般化吗？

（1）若∠C=90°，求证：△ABC的面积等于mn。

倒过来思考呢？

（2）若AC·BC=2mn，求证：∠C=90°。

改变一下条件……

（3）若∠C=60°，用m、n表示△ABC的面积。

【解析】设△ABC的内切圆分别与AC、BC相切于点E、F，CE的长为x，根据切线长定理，得：AE=AD=m，BF=BD=n，CF=CE=x。

证明：（1）如图7，在Rt△ABC中，根据勾股定理，得（x+m）2+（x+n）2=（m+n）2，整理，得x2+（m+n）x=mn，所以S=AC·BC=（x+m）（x+△ABCn）=x2+（m+n）x+mn］mn+mn）=mn。

图7

证明：（2）由AC·BC=2mn，得（x+m）（x+n）=2mn，整理，得x2+（m+n）x=mn，∴AC2+BC2=（x+m）2+（x+n）2=2［x2+（m+n）x］+m2+n2=2mn+m2+n2=（m+n）2=AB2，根据勾股定理逆定理可得∠C=90°。

解：（3）如图8，过点A作AG⊥BC于点G，在Rt△ACG中，AG=AC·sin60°=x+m），CG=

在Rt△ABG中，根据勾股定理可得［3

2

（x+m）］2+［（x+n）-x+m）］2=（m+n）2，整理，得

x2+（m+n）x=3mn，∴S△ABC=BC·AG=×（x+n）·x+m）=x2+（m+n）x+mn］=（3mn+mn）=3mn。

图8

【点评】本题是南京市中考数学的压轴题，此题是对教材习题的深度挖掘。做这道中考题，同学们更应该汲取的是其中的学习方法。研究一个问题要从特殊到一般，思考不受局限，运用多种角度、逆向思维，会有很多精彩的发现。事实上，本题可以进一步推广到一般三角形中：△ABC的内切圆与AB相切于点D，AD=m，BD=n，∠C=α，则S△ABC=，同学们到了高中可以进一步验证这个结论。