数学问题解决教学设计的新视角——基于提高数学抽象能力

叶金鑫 张 昆

淮北师范大学数学科学学院 (235000)

问题是数学的心脏，解题教学是数学课堂教学的重要形式之一，针对数学问题的特怔，在课堂上引发师生之间，生生之间的讨论与交流，充分利用相关的数学知识和思想方法，寻找解决问题的策略和方法，拓展学生的解题思路，优化学生的思维品质，是解题教学的理想追求.有些问题比较新颖，同学们从表象中难以看出玄机，这时体现了提高数学抽象能力的重要性.下面笔者来具体谈谈数学抽象能力.

1.数学抽象能力概念的界定

所谓抽象，通常是指从众多的事物中抽取出共同的和本质性的特征，而舍弃其非本质特征的思维过程.数学抽象则是指在数学活动中，抽取出一般的基本概念、本质特征以及运算规律等数学属性的思维过程.数学抽象是一种高级的数学思维能力，也是数学能力的核心.数学抽象能力具体表现为：发现在普遍现象中存在差异的能力，在各类现象间建立联系的能力，分离出问题的核心和实质的能力，由特殊到一般的能力，从非本质的细节中使自己摆脱出来的能力，把本质的与非本质的东西区分开来的能力，善于把具体问题抽象为数学模型的能力等等方面.在数学的学习中，数学抽象思维能力的培养是以数学对象或数学内容为基础，抽取同类事物中共同的、本质的属性或特征，形成新的事物的思维过程.数学抽象思维能力的基本方法类似于自然科学的思维方法，如观察、实验、类比、归纳，也类似于社会科学的思维方法，如反驳、猜测、想象、直觉等.

2.培养学生数学抽象能力的作用

作为数学能力的核心，数学抽象在数学核心素养中占据最重要地位.甚至可以说，数学抽象是数学核心素养的基础.一方面，数学学习过程中需要学习者具备一定的抽象能力.由于数学具有抽象性的特点，学习者只有具备一定程度的抽象能力，才能对数学对象的认知实现质的飞跃.另一方面，数学的应用过程也对学习者的数学抽象素养有一定的要求.在数学的应用活动中，要求学习者能将所遇情境进行数学化和抽象化，并与已学数学知识相联系，最终利用数学知识解决问题并将问题还原回实际情况.这一系列的活动都是建立在数学抽象基础上的，所以，教师在教学活动中要特别注重对数学抽象能力的培养.学生抽象能力越高，在学习中的迁移能力就越强，对新的知识的理解和掌握也就越快.抽象是思维最重要的特点.因为只有通过抽象才能使人的认识由感性上升到理性，从而掌握事物的本质和规律.因此抽象的水平在一定程度上反映了学生的思维水平.如果学生的数学抽象能力提高了，他们的逻辑思维水平才会真正提高.从而使学生在数学的学习过程中能迅速抓住本质，提升学习效率，为以后的学习奠定基石.既然数学抽象能力对学生发展的作用如此之大，那么笔者从一道高考题出发，具体谈谈提高数学抽象能力对解题的益处，希望对老师们今后的教学有所帮助.

3.在数学解题活动中培养学生抽象能力

我们引入的这道高考题的例子，都是源于真实高三数学教师在复习课上所讲授的解题教学内容，只是为了行文表达的技术上需要，我们在不改变授课教师原来设计所生成的教学环节及联结这些环节的中介的基础上，在极少数地方作了改动.

例1 已知acosα+bsinα=c，acosβ+bsinβ=c，若cosα+cosβ=cosα·cosβ，求证c2-b2=2ac.

师：已知条件为acosα+bsinα=c①，acosβ+bsinβ=c②，若cosα+cosβ=cosα·cosβ③，我们该如何证明c2-b2=2ac④.

生1：这道题我是这样想的，告诉我们两个已知条件，我准备从等式①出发，因为涉及到sinα,cosα，自然想起了三角关系式sin2α+cos2α=1，如果要凑成三角关系式，那么可能要平方，于是我想对两边进行平方，再利用三角公式sin2α+cos2α=1进行替换，这样就只有一个未知数了，另一个式子也是如此，即(acosα+bsinα)2=c2，得到a2cos2α+2abcosαsinα+b2sin2α=c2，写到这步突然发现2abcosαsinα不好处理，于是…

师：这位同学想到这步已经很好了，他既然遇到2abcosαsinα不好处理，同学们能不能想一种既用到两边平方也不出现2abcosαsinα这种形式的方法.同学们可以讨论一下.

生：议论纷纷.

生2：老师，我发现只要把acosα或bsinα其中一个调到等式的另一边就可以了，这样就不会出现2abcosαsinα这种乘积的形式了，我们首先可以把bsinα放到等式的另一边，再两边平方，接着用三角公式sin2α+cos2α=1进行替换，这样就只出现一个未知数了，另一个式子也如此.

师:很好，结合以上两位同学的共同想法我来具体化一下

解：由题意得acosα-c=-bsinα,两边平方得(acosα-c)2=(-bsinα)2,展开得a2cos2α-2accosα+c2=b2sin2α,因为sin2α=1-cos2α,所以a2cos2α-2accosα+c2=b2(1-cos2α),整理得

(a2+b2)cos2α-2accosα+c2-b2=0⑤,同理可得(a2+b2)cos2β-2accosβ+c2-b2=0⑥.

师：接下来同学们该怎么办呢？大家可以分小组讨论一下.

课堂活动记录：学生你一言我一语的讨论着，有的还在纸上认真的演算...

生3：我们小组是这样想的，观察⑤⑥两式，我们发现了它们的相同点，它们除了cosα,cosβ不相同外，其它的都相同，我们想可不可以用一个未知数来代替，于是把cosα,cosβ看成是方程(a2+b2)x2-2acx+c2-b2=0的两个根，再根据方程根与系数的性质得出两根之和与两根之积，又因为已知条件等式③，我们可以得出两根之和与两根之积是相等的，这样就可以证明出这个问题.我来具体化一下过程，接着生2的想法，我接着写.

由上述⑤⑥两个式子可得cosα,cosβ是方程

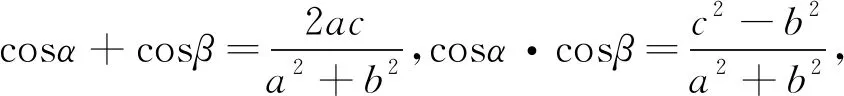
其实这一题到这里算是一种比较好的解法了，首先通过自己之前的知识经验把不熟悉的式子转化成具有相同形式的式子，再观察式子的相同点，进行抽象，把⑤⑥两个式子用⑦一个式子来表示，最后证明出结果.在解题过程中学生们初步接触用抽象方法来解决数学问题，在日常的解题教学中老师要时刻渗透这种抽象的思想，使得知识的形成，应用更具自然，流畅.让同学们掌握这种思想，使他们得到提升.在教学过程中又有学生提出这样的问题.

生4：像生1生2那种思路我一下子可能想不到，老师有没有其它简单点的思路呢?

师：确实，我们遇到难题都希望化繁为简，当看到复杂的解法时，往往会想如果有更简单的方法就好了，那请同学们利用我们刚刚学的抽象方法想想看有没有更简单的证明方法呢？

生：一片讨论声.

生5：我通过观察①②两式，发现两个式子的形式完全相同，利用方法一的思路，可以将①②两式进行抽象，得出一个式子ax+by=c，这里将cosα,cosβ抽象成x，sinα,sinβ抽象成y，由此又想到把三角公式sin2α+cos2α=1，抽象成x2+y2=1，联立两个式子，得出和方法一相同的式子(a2+b2)x2-2acx+c2-b2=0，后面的过程和方法一就相同了.

师：说的真好，听了生5的解题思路，现在我请一个同学来具体化一下思路.

这种解法相比于方法一可能更简单，不需要经过任何转化，只需要根据抽象法的要求，观察相同点，再把相同点用一个未知数来代替.这样省去转化中的繁琐计算，更有利于学生对数学的学习.由这道题的两种解法，同学们了解了在问题解决不出来的时候大家可以回过头来想想这个问题可不可以用抽象化来解题，或许对我们解决问题会有所帮助.

4.两种具体解法分析

由上述一道题的两种解法，我们可以得出提高抽象能力在我们日常解题中的重要性.不管是第一种解法在解题过程中的间接抽象，还是第二种解法在题目一开始就直接抽象，都要求我们对抽象能力有一定的理解和把握.下面笔者来具体谈谈这两种解法.

第一种解法：从题目本身出发，直接从已知条件入手，运用转化思想把题目转化成我们所熟悉的形式，这就是第一步移项得出的acosα-c=-bsinα，再两边平方得出(acosα-c)2=(-bsinα)2，其实这步是学生1和学生2经过多次移项的尝试得来的，如果稍有不慎就可能陷入学生1的囧境.所以这种解法对于解题能力稍弱的同学可能是困难的.接下来要用到一个三角公式sin2α+cos2α=1，把这个式子代入，整理出一个式子(a2+b2)cos2α-2accosα+c2-b2=0，同理可得另一个式子，(a2+b2)cos2β-2accosβ+c2-b2=0，观察这两个式子抽象出一个方程(a2+b2)x2-2acx+c2-b2=0，最后根据方程的性质证明出结果.这种解法相比较第二种解法多了前面的转化过程，也间接繁琐了计算，增加了思维的复杂程度，对于刚接触抽象法的学生来说是有点难以接受，很容易让他们对数学失去兴趣和信心.

第二种解法：从第一步就是观察等式①②，观察出相同点后把相同点用一个未知数来代替即抽象成ax+by=c，再把我们所熟悉的一个公式sin2α+cos2α=1，抽象成x2+y2=1，联立两个公式可得出结果(a2+b2)x2-2acx+c2-b2=0，后面的解法就和解法一一样了.这题不需要像第一题那样的繁琐计算，直接从已知条件出发，抽象出最一般的代表，得出结果.作为提高学生在数学问题解决中抽象能力的入门例题，这种解法能很快的让学生感受到数学解题中的抽象思想，从中体会到具备抽象能力的优势和益处，激发学生学好此类方法的兴趣，进而在不知不觉中形成解决问题的抽象能力.所以笔者认为要时时培养这种思想，在课堂教学过程中老师要潜移默化的渗透这种思想，这也是这题的精神所在.

这两种解法的不同点在于解法一是在过程中进行抽象而解法二是在一开始就进行抽象，解法一比解法二多了开头的转化.但两种解法的相同点都是要求学生掌握这种数学抽象的方法，进而提升数学抽象能力.从更有利于学生掌握这种抽象方法来说，笔者更倾向于第二种解法，因为从问题的一开始就需要学生们具有抽象化能力，直接从已知条件抽象，不需要繁琐的转化过程，这样也相对减少题目的运算量，简化了思维，更有利于学生们接受这种方法.不论哪种解法，都强调了数学抽象能力，而这种能力是很难培养的，需要教师在日常的解题教学中逐步去渗透这种思想.这一题的第二种解法也给我们教师一种启示，如果学生在以前就有了这种思想的培养，那这题就非常容易了，也避免了像第一种解法的繁琐计算.所以及早锻炼学生的这种能力，为学生以后的思维发展奠定基石.这也是笔者写这篇文章的意义所在.

5.简要的结论

由此，我们可以得到这样的结论：教师在进行数学教学设计时和在日常教学生的解题过程中都要时时刻刻的渗透“提高数学抽象能力”的思想.俗话说“多一点想就有可能少一点算”，这也是近些年高考命题的趋势，因此在平时的解题训练中，应倡导对问题进行适当的归类，掌握相应的求解方法，来为我们解题提供方便.总之，数学抽象能力的培养是一个长期的过程，其过程需要教师和学生大量的练习和尝试.作为教师，应该通过多种途径给学生提供锻炼的机会，而作为学生，应该主动积极地思考和总结，在具体和抽象之间多做转化，对所学内容勤于总结，最好能用自己的语言复述和整理，有意培养自己的数学抽象能力，为自己今后的数学学习打下良好的基础.