对“设而不求”的解答分析与思考

唐俊涛

江苏省吴县中学 (215151)

1.问题呈现

在高中数学解题过程中，有一类题型需要设置一些题目中没有直接给出的变量，而这些中间变量可以通过相应的化简变形进行消除、或整体代换，对最终的结果起到了重要的衔接作用，这就是我们常讲的数学中的“设而不求”.

而高中阶段我们最为熟悉的“设而不求”题目就是圆锥曲线中的一种解题方式，往往过程是：联列直线与圆锥曲线的方程，消元得到关于x或y的一元二次方程，设出直线与圆锥曲线的交点坐标(x1,y1),(x2,y2)，利用韦达定理得到x1、y1、x2、y2的关系，从而解决相应的问题.其实“设而不求”并非只是处理解析几何问题中的通性通法，在很多数学“板块”中都能适用.作为教师，对此应该要有全面的认识，不可以以偏概全，更不能绝对化.可是在实际课堂教学过程中，教师往往把“设而不求”变成了一种“固定的模式、不变的套路”，学生在解题过程中常常是“死记硬背、套用模式”.长此以往学生的解题能力并没有提高，相反如此长期训练还抑制了学生的思维发展，这样的教学未免有失偏颇.其实我们应该摒弃一些陈旧的、定势的思维，努力培养学生多元化的创新思维.

2.题型汇总

笔者将常见的设而不求问题进行了分类和总结，供大家参考，同时也希望能得到专家同行的指点.

2.1 解析几何中的设而不求

解析几何中的设而不求往往是为了避免坐标的繁琐，通过寻找横纵坐标之间的关系，从而简化运算的一种方案.

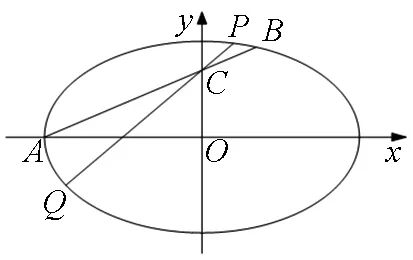
图1

例1 点A(-a,0),

(1)求椭圆的方程；(2)过点C任意作一条直线PQ与椭圆相交于P，Q，求PQ的取值范围．

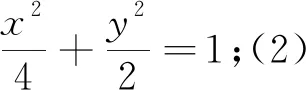
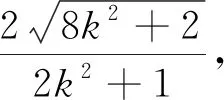
本题是典型“设而不求”在直线与椭圆中的应用.P(x1,y1),Q(x2,y2)的坐标在计算过程中没有具体去求出，而是利用韦达定理整体去求出PQ的表达式，从而进行求解.这是常见“设而不求”的应用，也是学生最熟悉的一种“设而不求”的题型.当然在利用韦达定理时应该先确保联立所得的二次方程有解，即△≥0.但上题中直线所过点C(0,1)在椭圆内部，所以可确保△≥0.

在解决此类题目时，学生解题的思路往往没有问题，关键在运算上会出现问题，所以此类问题教学教师需要放手让学生去独立求解，自行突破运算化简的“瓶颈”，这样考试中遇到类似问题时，学生就能从容应对，提高运算的准确性.

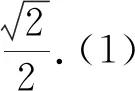
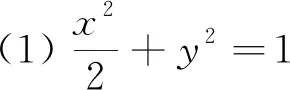
例2并不是圆锥曲线中常用的“设而不求”.若设出直线方程与椭圆方程进行联列后用韦达定理求解，则计算量会相当的大，而且表达式会比较繁琐,学生进行处理时往往会“半途而废”.反之如果设点坐标进行化简求解，虽然字母较多，但表达式相对简单，只需要合理的变形，突破要求量的“瓶颈”，解题就自然顺畅、简明很多.这也体现着“思维量大，运算量小”的特点，同时这也符合近几年来高考压轴题的命题趋势.

当然在解析几何中，设直线与设点往往都是可行的，这也需要学生通过一定的分析来选择适当的解决方案，从而避开繁琐的运算.

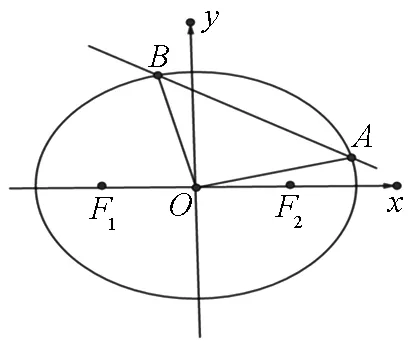
图2

此题处理不仅可通过设直线求解，同时还可利用设点的坐标求解，当然在具体解答时可发现设点坐标相比设直线运算量要小，但是思维量要大.这就需要学生数学感觉更强，对选择切入点的能力要求更高。正所谓“条条大路通罗马，需要分清远和近，多多思考找捷径，重视思维提能力.”

2.2 三角函数中的设而不求

当然在“三角函数”板块中当遇到所求角度并不是特殊角时，有时也需要设“辅助角”来进行过渡，这也是“设而不求”的方法.

解析：函数f(x)=2msinx-ncosx=

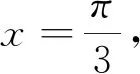
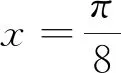
此类题型的特点就是题中“合一变形”后φ不是特殊角，所以学生在解题中就会陷入困境.事实上，只要对φ“设而不求”，让其满足题中条件即可.

2.3 函数零点中的设而不求

对于某些复杂函数的零点问题，并不能简单的通过求解相应的方程来进行处理，此时该函数零点可以先将其设出，通过该零点满足的方程或等式，整体代换，达到设而不求的效果，从而达到简化数学运算的目的.

例4 (2013年全国卷理科)已知函数f(x)=ex-ln(x+m).(1)x=0是f(x)的极值点，求m，并讨论f(x)的单调性；(2)当m≤2时，证明：f(x)>0.

解析：(1)略；(2)函数f(x)的定义域为(-m,+∞),由m≤2，可知f(x)=ex-ln(x+m)≥ex-ln(x+2)，所以原命题就变成只需证明ex-ln(x+2)>0.

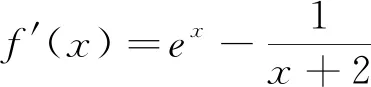
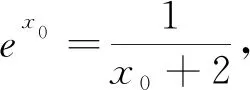
2.4 方程同解中的设而不求

方程的根与函数的零点从数的角度是统一的，方程的根与函数图像交点则是从形的角度是统一的.所以当图像的交点相同时，则它们所对应的方程也应该是同解的.

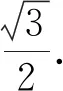
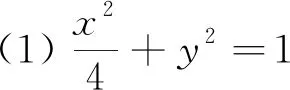
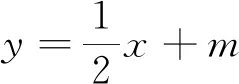
本题中涉及的方程根的设而不求，并没有用到前面所讲的韦达定理来解题，而是利用了两个方程的解相同，所以通过方程的对应系数相等或成比例解答，这样的解题就避开了求解P、Q坐标这样繁琐的步骤.

3.总结反思

综上分析，笔者认为只在圆锥曲线中涉及到“设而不求”是狭隘的，在三角、函数、方程等数学“板块”中也常常会出现需要通过“设而不求”来解决的题型.

教师在教学“设而不求”内容的重点就是让学生首先要了解“设什么”，“怎么设”，这是“设而不求”的核心；其次列式后如何根据所得的等式中提取我们题目中关键的信息，从而过渡到所需要的结果，这里需要学生有一定的变形、化简、转化的能力，这就是教师在教学过程中的重点，学生学习的难点.

就“设而不求“本身而言，它具备广泛的应用性，教师在教学过程中应该拓宽学生的思维空间，不能让学生产生定势思维，应该引导学生全面地进行思考，独立地进行解答，将各个数学知识板块内容串联起来，高视角思考问题，同时还能够提升自身的解题能力与学科素养.