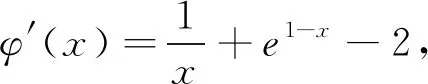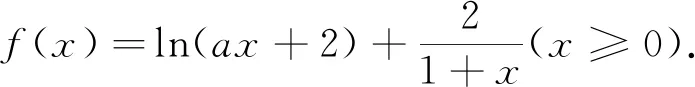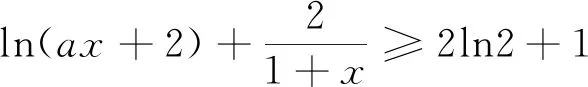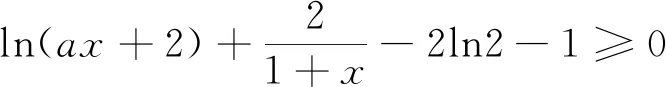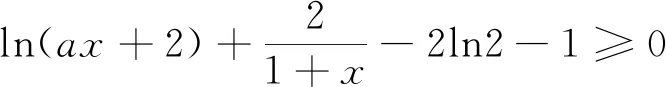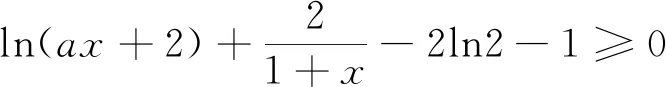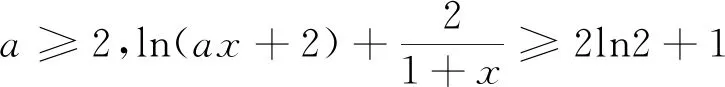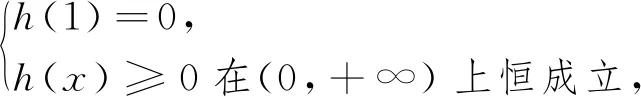两步法处理含参恒成立问题中参数取值范围的问题

杨艳萍

江西省九江第一中学 (332000)

解决含参数不等式恒成立中的参数范围问题，通常利用分离参数法，再求函数最值，从而求解，成为熟知的解题通法.而有一些含参数不等式其参数不能从解析式中分离出来，或分离参数后，解析式中含多个超越函数无法求其最值，这类含参数不等式恒成立求参问题，涉及的知识面广，综合性强，同时数学语言抽象，讨论繁杂等，严重影响解题的速度，甚至会中断解题过程，导致“望题兴叹”.然而这类问题又是历年高考函数压轴题的热点和难点.高考过程中，在规定的时间内，如何保质保量完成解题的任务，解题方法的选择尤为重要.为此，笔者经过研究得出了程序化的解题过程，只要按两步操作即可，希望对大家有所启迪.

例1 (2018九江三模理21)已知函数f(x)=xlnx+a·e1-x(a∈R)．

(1)当a=1时，求函数f(x)的最小值；

(2)若f(x)

分析：不等式f(x)

解析：(1)略.(2)f(x)

则函数h(x)在1的某个右领域(1右侧小范围)内必定单调递减，即存在ε>1，当x∈(1,ε)时，∴h(x)单调递减，即h′(x)=lnx+1-a·e1-x-2a(x-1)≤0在[1,ε]内恒成立，∴h′(1)=1-a≤0，即a≥1.

第二步：下证：当a≥1时，h(x)<0在(1,

点评：第一步为第二步做铺垫，第二步：证：当a≥1时，h(x)<0在(1,+∞)内恒成立,有两种方法可供选择，方法一：直接证当a≥1时，h(x)<0在(1,+∞)内恒成立；方法二：证当a≥1时，h′(x)≤0在(1,+∞)内恒成立；观察h(x)和h′(x)的解析式，不难发现借助不等式a≥1，h′(x)可放大(消参数a)，即h′(x)≤φ(x)(消参数a)，从而只需证明不含参数的φ(x)≤0即可.

(1)当a=2时，求f(x)的最小值；

(2)当f(x)≥2ln2+1恒成立，求实数a的取值范围.

两步求解：

例3 已知函数f(x)=mxlnx.

(1)当m>0时，求函数F(x)=f(x)-x+1的单调区间;

(2)若对任意的x∈(0,+∞),f(x)≥x-1恒成立，求实数m的值.

分析：不等式mxlnx-x+1≥0，易发现当x=1时，不等式左边恰好等于零，又不等式mxlnx-x+1≥0在(0,+∞)上恒成立，画函数简图可知x=1是函数h(x)=mxlnx-x+1,x∈(0,+∞)的极小值点，第一步h′(1)=m-1=0得“对任意的x∈(0,+∞),f(x)≥x-1恒成立”的必要条件m=1；第二步再证充分性.

解：(1)略.(2)对任意的x∈(0,+∞),f(x)≥x-1恒成立，即mxlnx-x+1≥0在(0,+∞)上恒成立，令h(x)=mxlnx-x+1,x∈(0,+∞).

两步求解：

第一步：由于

第二步：下证当m=1时，h(x)≥0在(0,+∞)上恒成立.

当m=1时，h′(x)=lnx，当x>1时，h′(x)>0,当0

点评：第一步观察函数的零点、极值点等特殊点，借助函数的极小值点x=1确定“对任意的x∈(0,+∞),f(x)≥x-1恒成立”的必要条件m=1；第二步将m=1代入易证不等式xlnx-x+1≥0在(0,+∞)上恒成立.

超越函数(三角函数、对数函数以及变量在无理数幂所表示的函数)与初等函数经过四则运算形成的不等式，对于这类不等式高中阶段只能借助观察法取特值求解，所以解答这类题型时迅速确定自变量取哪个特值是关键.命题人在命题时一般会将自变量的特值作为区间端点或隐藏在给定的区间中.本文从命题角度入手，利用区间端点得到不等式恒成立的必要条件，或观察不等式中函数的特征可以确定自变量的特值，借助这个特值得到不等式恒成立的必要性，再证不等式恒成立的充分性，从而确定参数的范围.