经典风险模型中破产变量的联合分布

苏必豪，李婧超

深圳大学数学与统计学院，广东深圳 518060

近年来，学界对保险风险模型的破产相关变量做出大量研究．GERBER等[1]对破产时间、破产时赤字和索赔数等问题进行研究．虽然破产概率仍是破产理论的焦点，但研究破产相关变量及其之间的关系更具有一般性．经典风险模型的研究表明，当破产发生时，若初始盈余对最终破产概率的影响不可忽略，则破产概率密度是正偏斜的，且偏斜度至少为0.5%[2]．类似地，在相同情况下直到破产发生时，索赔次数的概率函数是正偏斜的[3]．这些结果说明，当破产发生时，总索赔额分布的偏度可能是正的，本研究将证明该结论成立．

虽然已经有许多学者对破产前总索赔的预期折现额进行研究[4-5]，但关于破产时总索赔额的研究却不多，唐应辉等[6]根据个体索赔额分布函数的性质，研究个别风险模型中总索赔额分布函数的界值问题．本研究将揭示破产时的总索赔额与破产时间和破产赤字密切相关．尽管破产时的赤字分布并未体现保险公司在破产之前的支出额分布情况，但由破产时间的分布可知保险公司直到破产前的收入．根据破产时间和破产赤字的联合分布，可研究破产前总索赔额的分布等性质．破产时总索赔额的分布给保险人指明，不同程度的支出对应发生破产的可能性．HUANG等[7]讨论盈余第一次达到一定水平时的拉普拉斯变换，RABEHASAINA等[8]研究在Sparre Andersen过程中，破产时间和破产时总索赔量的联合分布，得出拉普拉斯变换的表达式，但未能有效对其结果做逆变换．在初始盈余为0的情况下，做逆变换并不是一个获得破产相关变量分布的简单方法[9-10]．本研究采取较为直接的方法，得到联合密度的显式表达式．通过对破产时间和破产时赤字的联合概率密度函数进行函数变换，得到截止至破产时的总索赔额与其他破产变量，如截止破产时的总索赔次数、破产时间及破产时赤字的联合概率密度，并且以个体索赔分布为指数分布以及其他可分解型的指数族分布的情况进行举例说明．

1 符号表示

2 包含S(Tu)的联合概率密度

考虑包含随机变量S(Tu)的联合概率密度．假设在时间t时，发生第n次索赔，此时破产发生，且破产的集体索赔额为x． 因此，

Pr(Tu≤t,N(Tu)=n,S(Tu)≤x)=

(1)

x>c+ct，t>0， 且

vn(u,x-ct-u,t)

w(u,x,t)=v(u,x-ct-u,t)

(2)

由(Tu,Yu)的概率密度，可求出(Tu,S(Tu))的概率密度．DICKSON 等[11-12]给出有关(Tu,Yu)概率密度的显式解．为得到wn(u,x,t)， 运用 DICKSON[13]给出的vn(u,y,t)公式，当u>0， 有w1(u,x,t)=λe-λtp(x)． 则对n=1,2,3,…有

pn*(ct-z)p(z+x-ct)dz

(3)

pj*(u+cs)

wn+1-j(0,x-u-cs,t-s)ds

(4)

通过式(3)和式(4)可获得包含2个变量的联合密度，对n求和得(Tu,S(Tu))的联合概率密度，对t积分得(N(Tu),S(Tu))的联合概率密度． (Tu,S(Tu))的联合概率密度可表示为

g(ct-z,t)p(z+x-ct)dz

(5)

且对u>0，

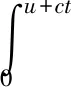
(6)

(7)

(8)

利用联合概率密度函数求S(Tu)的边缘概率密度较为复杂．然而，若定义

S(Tu)≤x)

(9)

对第1次索赔的时间和数量进行调整，得

(10)

对于存在显示表达式的ψ(u)， 式(10)中积分的性质不允许通过标准方法来求解Ω(u,x)的索赔大小分布．第2个标准方法是做逆变换，但仍非获得S(Tu)密度的有效途径．

2.1 指数索赔

首先， 考虑单次索赔额为指数分布， 即p(x)=αe-αx,x>0的情况，其结果在文献[14]中详细说明，v(u,x,t)=w(u,t)αe-αx， 因此，w(u,x,t)=w(u,t)αe-α(x-ct-u)． 文献[11]对于w(u,t)可得(Tu,S(Tu))的联合概率密度为

(11)

其中，x>u+ct，t>0， 且

为v阶的修正Bessel函数．图1给出对于2个不同u值时， (Tu,S(Tu))的联合概率密度函数图像．其中，t表示破产时间；x表示破产时的集体索赔额．由式(4)可得S(Tu)的概率密度．用求和形式写出Bessel函数，并根据(u+ct)n的二项展开式，当x>u， 有

(12)

(13)

图1 u=0, 20时w(u, x, t)的图像Fig.1 (Color online) w(u, x, t) charts when u=0, 20

同时，也可得(N(Tu),S(Tu))的联合概率密度，对任意的x>0， 运用式(7)可得

E(2n-1,λ,x/c)

(14)

对于u>0，x>u， 通过一些简单变换得

E(n+j-1,λ,(x-u)/c)-

E(2n+j-k-1,λ,(x-u)/c)} (15)

图2 当n=2,3,4,5, n=10和 n=20时，和的图像 and charts when n=2,3,4,5, n=10 and n=20

2.2 其他指数族索赔分布

只有特定几个类型的个体索赔分布才可以求出(Tu,Yu)联合分布函数的显式解，这些分布需满足以下性质[15]

(16)

其中， {ηj}为非负的实值函数； {τj}为概率密度函数．由此可推导出v(u,y,t)的形式为[16]

(17)

因此，可得

(18)

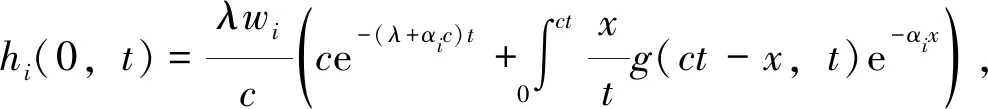
i=1,2,…,n.

(19)

结 语

本研究在经典风险模型下，研究破产时的总索赔额与破产时间和破产赤字的联合分布函数．根据破产时间和破产赤字的联合分布，研究破产前总索赔额的分布等性质．并选取指数索赔和几个其他特定的索赔类型为例，解出破产时总索赔额分布的具体表达式．指出不同程度的支出对应发生破产的可能性．