一类积分型集值映象列的公共不动点定理

张芯语，张树义，郑晓迪

(1.渤海大学数理学院，辽宁锦州 121013;2.锦州师范高等专科学校计算机系，辽宁 锦州 121001)

1 引言与预备知识

文献［1-2］中引入(C)g型非阿基米德概率2-距离空间的概念，讨论了可交换映象和集值映象列的公共不动点的存在性.文献［3-4］在(C)g型非阿基米德Menger概率度量空间中建立了包括Altman型在内的一些映象公共不动点的存在性定理.近些年来，文献［5-9］研究了几类非线性映象不动点的存在性.受上述工作启发，本文在(C)g型非阿基米德概率2-距离空间中建立一类积分型集值映象列公共不动点的存在性定理，从而改进和推广了文献［1-2］中的相应结果.

定义1［1］二元组(X，F)称为非阿基米德概率2-距离空间，如果X是非空集，F:X×X×X→D(D为全体分布函数)是满足以下条件的映象(Fx，y，z(t)表F(x，y，z)在t∈R处的值):

Ⅰ)Fx，y，z(0)=0，x，y，z∈ X;

Ⅱ) x，z∈ X，存在 y ∈ X，t0＞ 0，使得 Fx，z，y(t0) ＜ 1;

Ⅲ) 对 t ＞ 0，Fx，y，z(t)=1 当且仅当 x，y，z∈ X 中至少有二元相等;

Ⅳ)Fx，y，z=Fx，z，y=Fy，z，x，x，y，z∈ X;

Ⅴ) 若 Fx，y，u(t1)=1，Fx，u，z(t2)=1，Fu，z，x(t3)=1，则 Fx，y，z(max{t1，t2，t3})=1，x，y，z∈ X.

定义2［1］映象Δ:［0，1］3→［0，1］称为三角范数，如果满足以下条件:

ⅰ) Δ(a，1，1)=a，a ∈［0，1］;

ⅱ)Δ(a，b，c)= Δ(a，c，b)= Δ(c，a，b)，a，b，c∈［0，1］;

ⅲ) 当 d ≥ a，e≥ b，f≥ c时，有 Δ(d，e，f) ≥ Δ(a，b，c);

ⅳ)Δ(Δ(a，b，c)，d，e)= Δ(a，Δ(b，c，d)，e)，其中 a，b，c，d，e，f∈［0，1］.

定义3［1］三元组(X，F，Δ)称为非阿基米德Menger概率2-距离空间，若(X，F)是一非阿基米德概率2-距离空间，Δ是Δ-范数，且有

ⅵ)Fx，y，z(max{t1，t2，t3}) ≥ Δ(Fx，y，u(t1)，Fx，u，z(t2)，Fu，y，z(t3))，t1，t2，t3∈［0，!)，x，y，z，u ∈ X.

设 Ω ={g g:［0，1］→［0，!) 连续、严格递减，g(1)=0，g(0) ＜ +!}.

定义4［1］非阿基米德概率2-距离空间(X，F，Δ)称为(C)g型非阿基米德概率2-距离空间，如果存在 g ∈ Ω，使 x，y，z，u ∈ X，t≥ 0，有

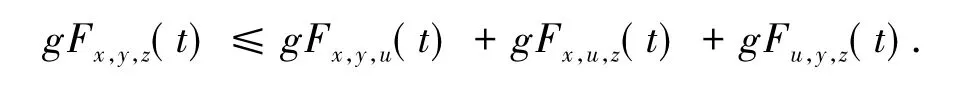
本文中假设(X，F，Δ)是完备的(C)g型非阿基米德Menger概率2-距离空间，Δ是连续的t-范数.

定义 5［1］设 A X，称 A是概率有界的，如果 a ∈ X，t ＞ 0，有 δ(A，g，t) ＜ +!，其中 δ(A，g，t)=g［Fr，y，a(t)］.用 W 表示 X 中一切非空闭的概率有界集合.

定义 6［1］对 A，B ∈ W，x，a ∈ X，定义

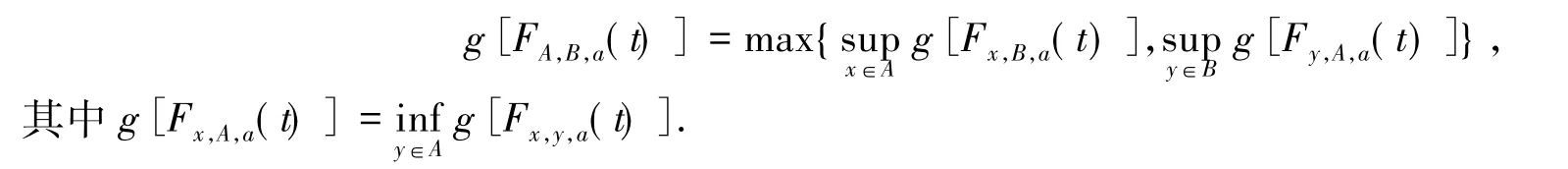
定义7h1{h h:［0，+!)→［0，+!)不减、右连续，且(t) ＜ !，t≥0，其中hn(t)表h(t)的n次迭代函数}，H1{H H:［0，!)5→［0，!) 右连续，对每一变量是非减的函数，t∈［0，!)，max{H(t，t，t，a1t，a2t) a1，a2∈ 瓔 ，a1+a2=2}=h(t) 满足 h1，其中瓔 为自然数集合}.

引理 1［1］设 A ∈ W，x，y，a ∈ X，则

ⅰ)g［Fx，A，a(t)］=0，a ∈ X，t ＞ 0x ∈ A;

ⅱ)g［Fx，A，a(t)］≤ g［Fx，y，a(t)］+g［Fx，A，a(t)］+g［Fy，A，a(t)］，t≥ 0;

ⅲ) 对任意 A，B ∈ W，如果 x ∈ A，则 g［Fx，B，a(t)］≤ g［FA，B，a(t)］，a ∈ X，t≥ 0.

引理 2设 h ∈ h1，{xn} 为 X 中序列，如果( τ)dτ≤ h(τ)dτ，a∈X，t≥ 0，则 m ≥ 0，t≥ 0，有(τ)dτ =0，其中 ψ:R+→R+是勒贝格可积与可和的:a，b∈R+，(τ)dτ+(τ)dτ，且(τ)dτ＞ 0，ε ＞ 0.

证明:由条件有

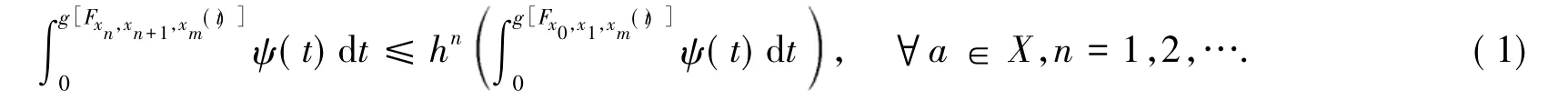
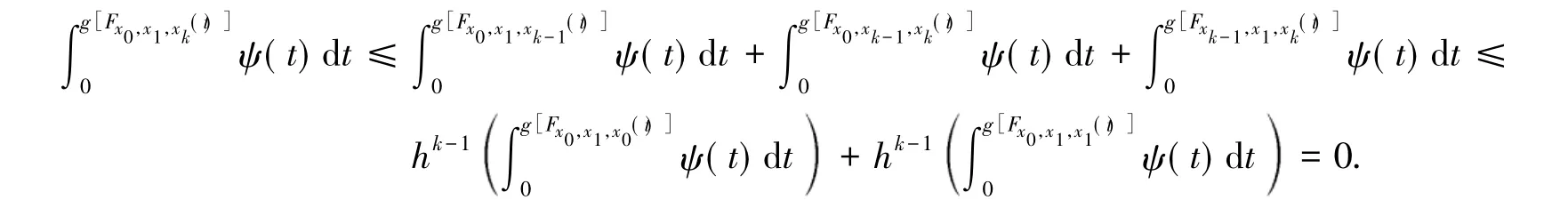
引理 3［1］设 H ∈ H1，则

1)h(t) ＜ t，t ＞ 0;

2) 若 t≤ h(t)，t≥ 0，则 t=0.

2 主要结果

定理1设为集值映象列，对 i，j∈ 瓔+(正整数集)，i≠ j，x，y，a ∈ X，t ＞ 0，有

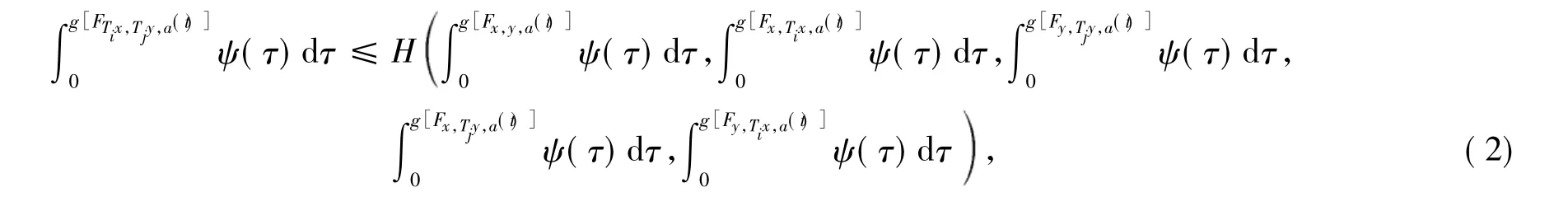
其中H∈ H1，ψ:R+=［0，!) → R+是勒贝格可积与可和的:a，b∈ R+，(τ)dτ≤(τ)dτ+τ)dτ，且τ)dτ＞ 0，ε ＞ 0.再设对x∈X，n∈瓔+及u∈Tnx，存在v∈Tn+1u，使a∈X，t＞ 0，( τ)dτ≤(τ)dτ，则存在 x*∈ X，使得 x*.

证明:任取x0∈X，取x1∈T1x0∈W，由定理1假设条件知，存在x2∈T2x1∈W，使a∈X，t＞0，有( τ)dτ ≤(τ)dτ.同样存在x3∈T3x2∈W，使a∈X，t ＞ 0，有(τ)dτ=(τ)dτ.重复上述过程，可得一序列{满足下述条件:xn∈Tnxn－1，a∈X，t ＞ 0，n 1，2，…，

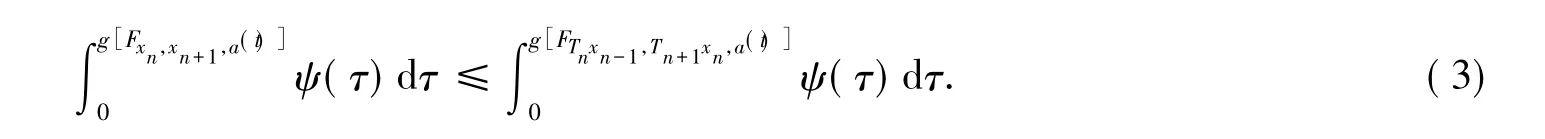
下面证明{xn}为X中Cauchy列.事实上，对n∈瓔+，a∈X，t＞0，由式(2)、(3)及引理1知

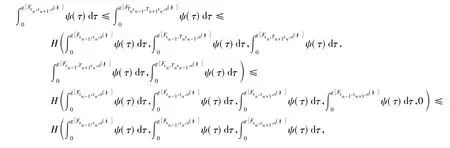
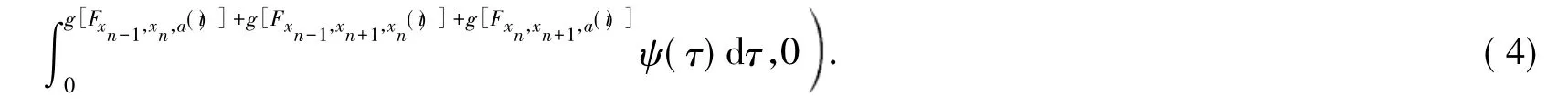
取 a=xn－1，由式(4) 得

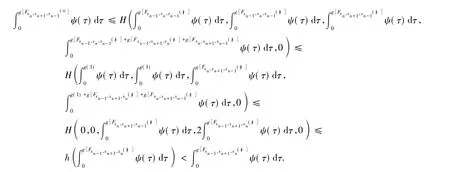
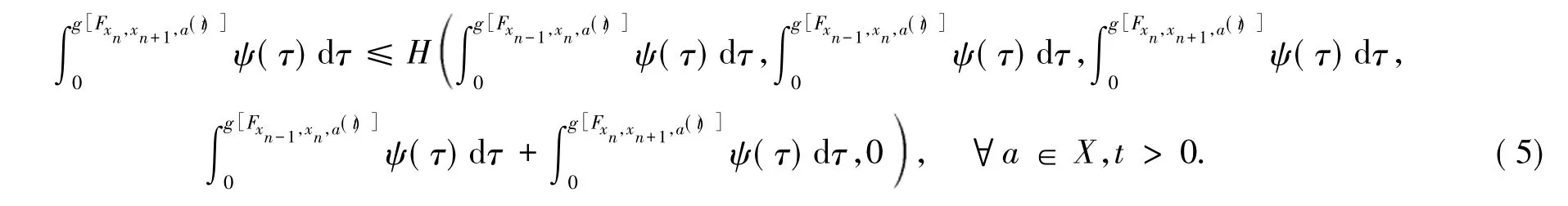
如果存在 t0＞ 0，a0∈ X，使( τ)dτ ＞(τ)dτ，则由式(5) 知

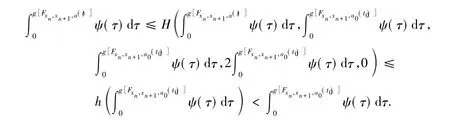
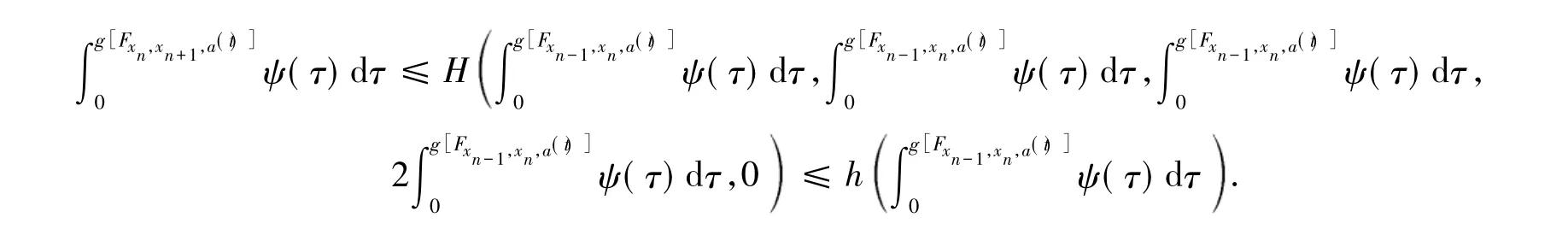
据此由引理 2 知 n，m ∈ 瓔+，有(t)dt=0.下面证{xn} 是X中的Cauchy列.m，n∈ 瓔+，n≤ m，有

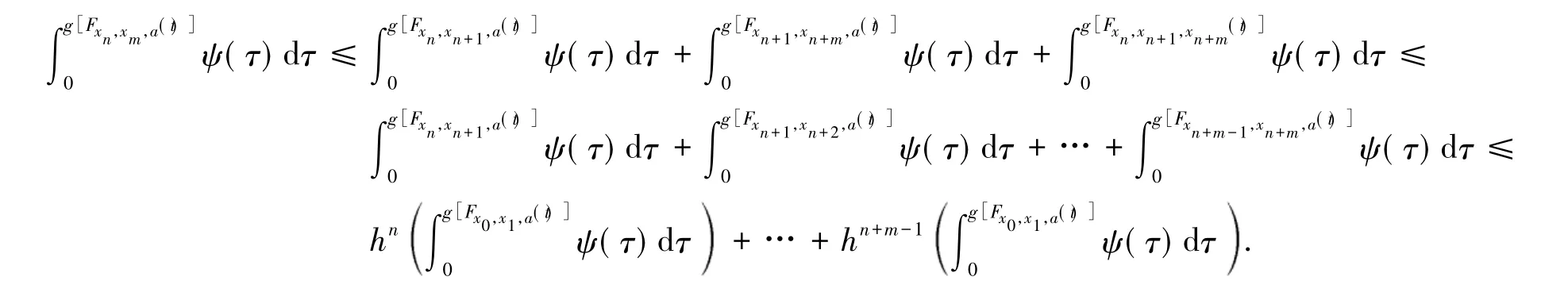
在上述不等式两端令n，m→!，并注意到H∈H1，易得(τ)dτ=0，a∈X，t＞ 0.由于g是连续的、严格减的，且g(1)=0，故知{xn}为X中Cauchy列，因X完备，故可设xn→x*∈X(n→!).下面证明x*是{的公共不动点.对 j∈ 瓔+，a∈X，t＞ 0，由式(2)、(3)及引理1可得

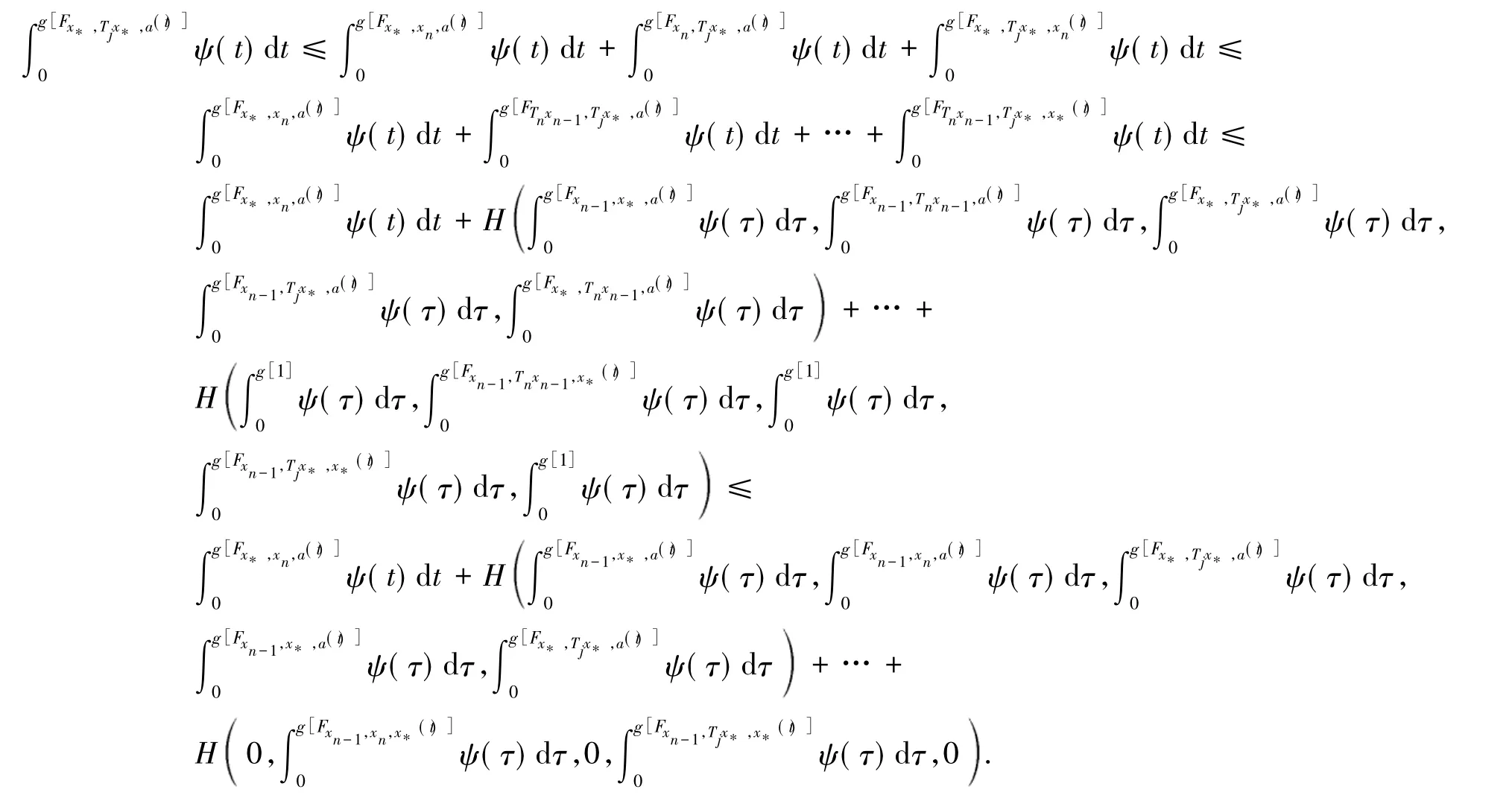
令n→!，并注意到H∈H1的右连续性，可得

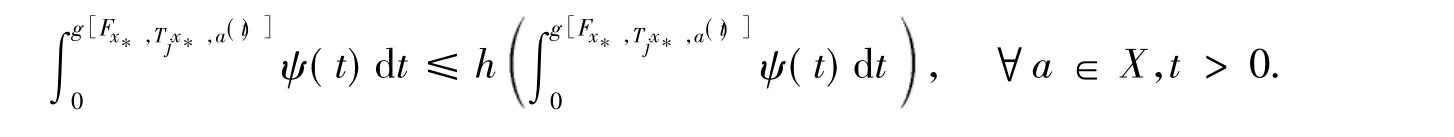
定理 2［2］设{:X → W 为集值映象列，对任意 i，j∈ 瓔+，i≠ j，任意 x，y，a ∈ X，t ＞ 0，有

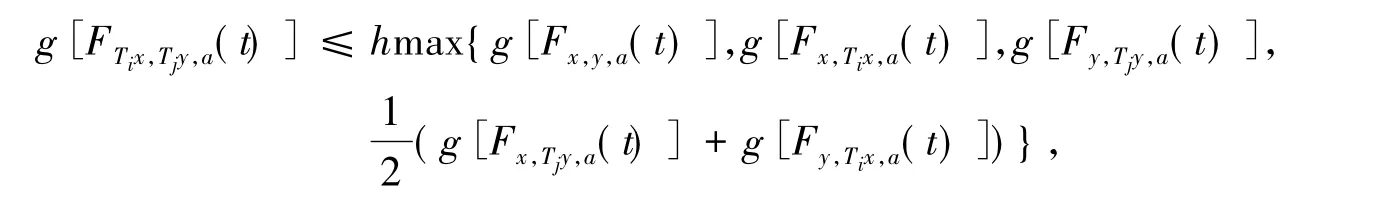
其中 h∈h1.再设对x∈X，n∈瓔+及u∈Tnx，存在v∈Tn+1u，使g［Fu，v，a(t)］≤g［FTnx，Tn+1u，a(t)］，a∈X，t＞ 0，则存在 x*∈ X，使得 x*.

证明:在定理 1 中取 ψ(t)=1，H(t，t，t，t，t)=h，则H对每一变量是非减的.注意到 max{H(t，t，t，a1t，a2t)a1，a2∈ 瓔+，a1+a2=2}=h(max{t，t，t，t})=h(t) 且 h ∈ h1，因此这样取的H∈H1，由定理1可得定理2.证毕.

推论1设{Ti}为 X 上的单值自映象，对 i，j∈ 瓔+，i≠ j，x，y，a ∈ X，t ＞ 0，有

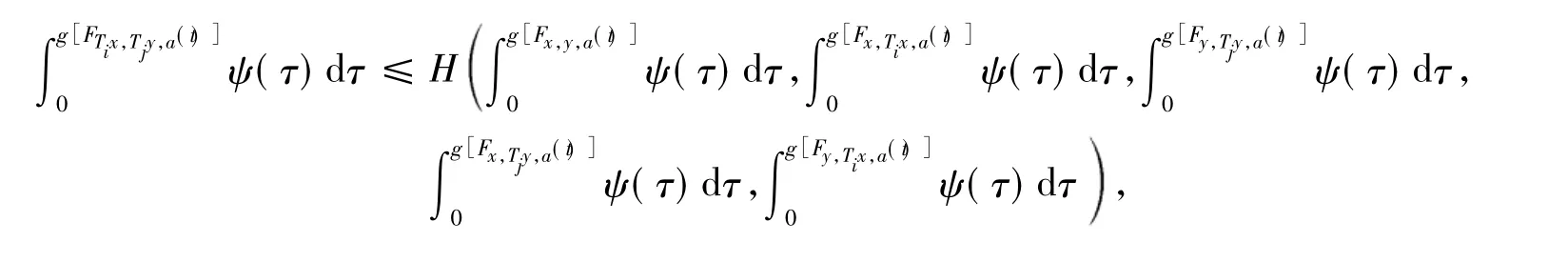
其中H∈ H1，ψ:R+=［0，!) → R+是勒贝格可积与可和的:a，b∈ R+，(τ)dτ≤τ)dτ+(τ)dτ，且(τ)dτ＞ 0，ε ＞ 0，则存在 x*∈ X，使 x*.