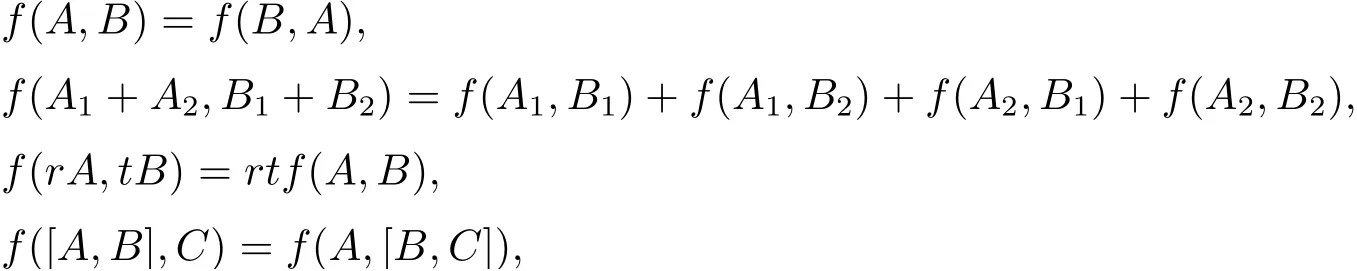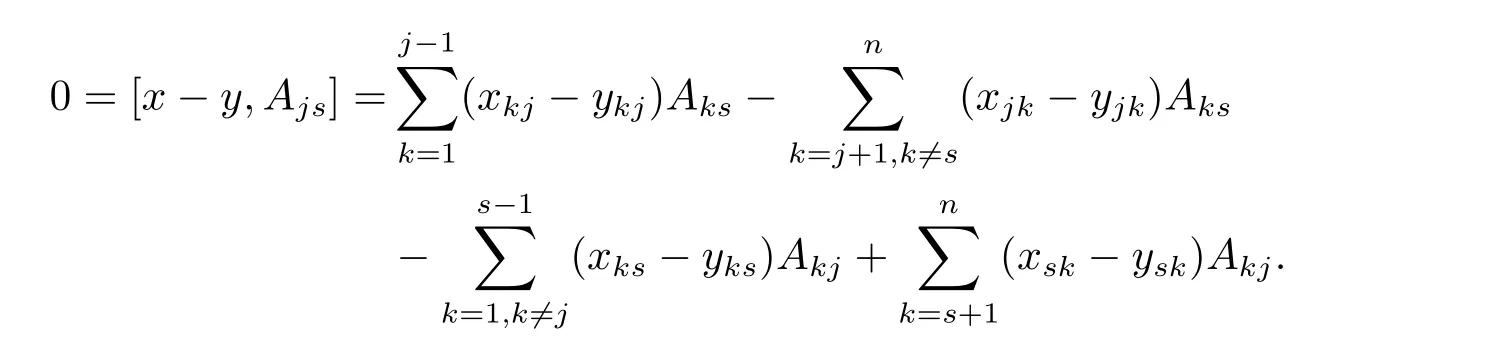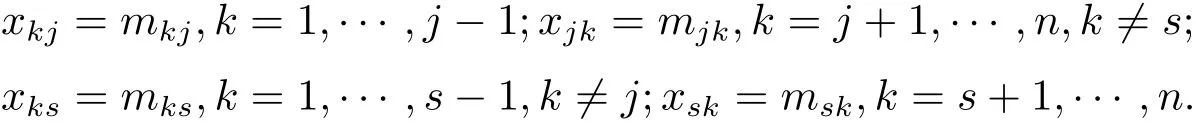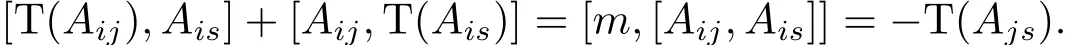交换环上反对称矩阵李代数的局部导子和2 - 局部导子
王 迪, 王 颖
(大连理工大学数学科学学院,辽宁大连116024)
1 引言
在上世纪90 年代, Larson, Sourour 和Kadison 在文献[1, 2] 中分别独立地提出了局部导子的概念. 之后, 学者们开始研究结合代数和非结合代数上的局部导子的结构. 设是Banach 空间,是上有界线性算子全体构成的代数. Larson 和Sourour 在文献[1] 中证明了上的局部导子都是导子; Kadison 在文献[2] 中证明了Von Neumann代数到它的对偶Banach 模的任一范数连续的局部导子是导子; 在文献[3] 中, 作者证明了C∗代数U 到Banach U - 双模上的局部导子是导子; 在文献[4] 中, 作者证明了因子von Neumann 代数的套子代数的任一范数连续线性局部导子是导子; 赵延霞和王丽在文献[5] 中证明了可交换环上上三角矩阵李代数的局部导子是导子; Ayupov 和Kudaybergenov 在文献[6] 中证明了特征为0 的代数闭域上有限维半单李代数上的局部导子是导子并且证明了维数大于3 的有限维幂零李代数上存在不是导子的局部导子.
2 - 局部导子可看作局部导子的一种非线性推广, 它的概念是由ˇSemrl 在文献[7] 中提出的. 令H 是无限维可分离Hilbert 空间, B(H) 是H 上所有有界线性算子构成的代数. ˇSemrl 在文献[7] 中证明了B(H) 上的所有2 - 局部导子都是导子; 2011 年, Ayupov 和Kudaybergenov 在文献[8] 中将ˇSemrl 的结论推广到任意Hilbert 空间上, 即当H 是任意Hilbert 空间时, B(H) 上的任一2 - 局部导子都是导子. 此外, Ayupov 等人还给出了其他代数上2 - 局部导子的结构. 例如, 在文献[9] 中, 作者们给出了交换正则代数上存在非导子的2- 局部导子的充分必要条件, 同时证明了交换正规代数上矩阵代数的2 - 局部导子是导子; 在文献[10] 中, 作者们证明了特征为0 的代数闭域上有限维半单李代数上的2 - 局部导子都是导子, 同时给出了有限维幂零李代数上2 - 局部导子不是导子的例子.
令R 表示有单位元1 的2 - 挠自由交换环, Ln(R) 表示R 上所有n×n 反对称矩阵构成的一个李代数. 在Ln(R) 上的李乘定义为[A,B] = AB −BA, 其中A,B ∈Ln(R).2009 年, 作者们在文献[11] 中证明了Ln(R)(n ≥3) 是完备李代数; 2013 年, 文献[12] 证明了Ln(R)(n ≥5) 上BZ 导子的分解式唯一, 进一步得出Ln(R) (n ≥5) 是完备李代数.由于Ln(R) 是完备李代数, 所以Ln(R) 上的导子都是内导子. 本文将利用这一结果证明Ln(R)(n ≥3) 上的2 - 局部导子和局部导子是导子.
2 基础知识
定义Ln(R) 上李乘为[A,B]=AB −BA, A,B ∈Ln(R). 设Eij为(i,j) 位置为1, 其余位置为0 的n 阶方阵. 令Aij=Eij−Eji, 则Aij∈Ln(R), Aij=−Aji, Aii=0. 根据Ln(R)上李乘的定义可知


定义2.1[13]令R 是有1 的交换环, L 是R 上的李代数. 若R - 线性映射φ:L →L 满足

则称φ 为导子. 特别的, 任意z ∈L, adz :L →L, adz(x)=[z,x],x ∈L 也是一个导子, 称这种形式的导子为内导子.
定义2.2[14]令R 是有1 的交换环, L 是R 上的李代数. 若满足
(i) Z(L)={x ∈L|[x,y]=0,y ∈L}=0,
(ii) L 的导子都是内导子,则称L 是完备李代数.
命题2.3(见文献[11,Theorem 3.2]) 令R 是有1 的2-挠自由交换环,那么Ln(R)(n ≥3)是完备李代数.
定义2.4[6]令R 是有1 的交换环, L 是R 上的李代数. 若R - 线性映射∆:L →L 满足: 对于任意x ∈L 都存在一个导子Dx( 与x 有关) 使得∆(x)=Dx(x), 则称∆为L 的局部导子.
定义2.5[10]令R 是有1 的交换环, L 是R 上的李代数. 若映射T:L →L 满足: 对于任意x,y ∈L 都存在一个导子Dx,y( 与x,y 有关) 使得T(x)=Dx,y(x), T(y)=Dx,y(y), 则称T 为L 的2 - 局部导子.
显然, 导子是局部导子, 也是2 - 局部导子. 反之, 不一定成立.
下文设T 和∆分别是Ln(R) 上的2 - 局部导子和局部导子.
由命题2.3 直接可得Ln(R)(n ≥3) 上的导子都是内导子, 因此对于任意A,B ∈Ln(R),存在MA,B∈Ln(R), 满足T(x) = [MA,B,A], T(y) = [MA,B,B]. 对于任意A ∈Ln(R), 存在MA∈Ln(R), 满足∆(x)=[MA,A].
3 局部导子
根据局部导子定义可得, 存在A ∈Ln(R) (n ≥3) 使得∆(A12) = [A,A12]. 令∆−adA, 则显然, 如果是导子, 那么∆是导子. 下文中用∆表示并将证明∆是一个导子.
引理3.1设∆是L3(R) 上的局部导子. 若∆(A12)=0, 则∆是导子.
证显然,A12,A13,A23可作为L3(R)的一组基.根据局部导子的定义,存在x,y ∈L3(R),使得∆(A13)=[x,A13], ∆(A23)=[y,A23]. 设

那么∆(A13)=−x1A23+x3A12, ∆(A23)=y1A13−y2A12.
对A12+A13, 存在m ∈L3(R), m = m1A12+m2A13+m3A23, 使得∆(A12+A13) =[m,A12+A13]. 因为∆是线性映射,所以∆(A12+A13)=∆(A12)+∆(A13),即[m,A12+A13]=0+[x,A13] = [x,A13]. 将m 和x 的基底表示代入等式, 整理得x3= m3= 0. 同理, 对A12+A23和A13+A23分别进行如上操作可得y2=0 和x1=y1. 所以

令∆1= ∆−ad(x1A12), 那么∆1(A12) = ∆1(A13) = ∆1(A23) = 0, 所以∆1= 0, 即∆=ad(x1A12). 因此L3(R) 上的局部导子∆是导子.
在Ln(R)(n ≥4) 中, 当3 ≤j ≤n 时, 由局部导子定义可得, 存在

使得

引理3.2设∆是Ln(R)(n ≥4) 上的局部导子. 若∆(A12) = 0, 那么存在m ∈Ln(R),令∆1=∆−adm, 使得

证在引理3.2 的证明中, 始终假设





由式(3.5) 第一个式子和式(3.6) 可得

令m=aA12, ∆1=∆−adm. 将(3.7) 和(3.8) 式分别代入(3.3) 和(3.4) 式, 得

此时∆1(A12)=0, 且∆1仍然是一个局部导子.


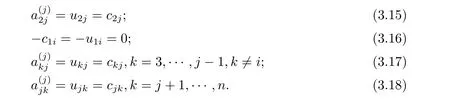

式子展开后可得

将(3.14)–(3.21) 式代入(3.11)–(3.13) 式, 可得
引理证毕.
定理3.3Ln(R)(n ≥3) 上的局部导子∆是导子.
证由引理3.1 可知, L3(R) 上的局部导子都是导子, 所以只需证明n ≥4 时结论成立.
因为∆1是线性映射, 所以如果对基底中任意两个元素Aij, Akl, 1 ≤i,j,k,l ≤n 都满足以下等式

则对任意x ∈Ln(R), y ∈Ln(R), 都有[∆1(x),y]+[x,∆1(y)] = ∆1([x,y]) 成立, 即∆1是导子. 现将基底分为四部分: A12, {A1p}3≤p≤n, {A2p}3≤p≤n, {Apq}3≤p 其中3 ≤i,j,k,l ≤n, 且i,j,k,l 互不相等. 以下验证第7 个等式成立, 不妨假设i 所以 由以上可得等式[∆1(Aij),Ail]+[Aij,∆1(Ail)]=−∆1(Ajl)成立, 其余等式类似可得. 因此∆1是导子, 根据命题2.3 可知存在X ∈Ln(R), 使得∆1=adX. 所以 即∆是一个导子. 定理得证. 引理4.1Ln(R)(n ≥3) 上的2 - 局部导子是线性映射. 证用tr(X) 表示矩阵X 的迹, 即X 的对角元素之和. 令f(A,B) = tr(AB),A,B ∈Ln(R), 则 其中A,B,A1,A2,B1,B2∈Ln(R), r,t ∈R. 由以上可得f 是Ln(R) 上非退化的对称双线性型. 设T 是Ln(R)(n ≥3) 上的2 - 局部导子, 那么对于任意A,B,C ∈Ln(R), 有 所以T(A+B)=T(A)+T(B). 对于任意A ∈Ln(R),r ∈R,存在MA,rA使得T(A)=[MA,rA,A],T(rA)=[MA,rA,rA],显然T(rA)=rT(A). 因此T 是线性映射. 引理得证. 定理4.2Ln(R)(n ≥3) 上的2 - 局部导子是导子. 证由引理4.1 知T 具有线性性,因此只需证明[T(Aij),Akl]+[Aij,T(Akl)]=T([Aij,Akl])成立即可. 分两种情况证明. (i) 当[Aij,Akl]=0 时,根据2-局部导子定义,存在m ∈Ln(R),使得T(Aij)=[m,Aij],T(Akl)=[m,Akl], 那么 等式成立. 满足T(Aij) = [x,Aij] = [m,Aij], T(Ais) = [y,Ais] = [m,Ais], T(Ajs) = [x,Ajs] = [y,Ajs]. 因此可得 将上式各项展开可得 所以 定理得证.
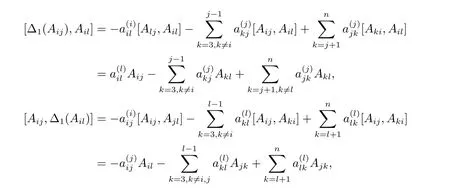


4 2 - 局部导子