三谈好的解题教学应“四有”*——以“正弦定理、余弦定理的应用”复习课为例

(大厂高级中学,江苏 南京 210044)

无论是平时的习题课，还是高三的复习课，数学解题教学都是数学教学中不可或缺的课型．基于实践，笔者曾用两个课例说明什么是“好的解题教学”，提出好的解题教学要“有想法——为什么选这道题”“有选择——怎么想到解题方法的”“有优化——能不能优化思路和方法”“有反思——思考是否存在解法的规律性”，简称“四有”[1-2]．

通过实践与反思，笔者进一步认识到：在解题教学中，教师可以搭建适当的“脚手架”，让学生体会数学问题的来龙去脉，发现数学知识结构中新的问题，积极尝试提出问题，进而分析和解决问题．这样做能调动学生的解题积极性，更重要的是学生深度参与了数学解题的过程．基于这样的认识，笔者第三次与读者分享“好数学教学”案例——“正弦定理、余弦定理的应用”复习课.本课例是笔者所在区工作室与某中学的联合教研活动之一，授课对象为高二学生，基础较好，在此之前已复习了三角函数图像与性质、恒等变换．

1 教学简录

1.1 有想法——常规开局，变式深入

1.1.1 基础训练

教师以一组基本题练习开始本节课，接着巡视学生的完成情况，待学生基本做好后进行简单反馈．如已知什么，求什么(为归纳“解三角形”的基本类型作准备)，用了哪些基本结论(公式)……对话中教师逐一板书本节课复习的3个公式：正弦定理、余弦定理和三角形面积公式．

笔者习惯于先练习后归纳，让学生在练习中唤醒记忆，在归纳中重读课本，使得所学基础知识前后一致、逻辑连贯．个别问题适当追问，如第2题，笔者巡视后发现学生都是通过余弦定理列一元二次方程来求c．

师：已知两边一对角，同学们都是利用余弦定理列方程得到c2-2c-3=0，解得c=-1(舍去)或c=3．能不能用正弦定理呢？

生(众)：能．

师：为什么不用呢？

生(众)：比较繁，要先求sinC，再由正弦定理求c．

师：关键是求sinC的过程中涉及角B范围的估计．怎么估计角B的范围？

生1：因为a>b⟺A>B，所以B为锐角．

师：我们称这类问题为“解三角形”.解三角形的主要工具是正弦定理、余弦定理和面积公式(已板书)，这就是本节课的主题．根据这组练习，解三角形有哪些类型？

师生总结类型，如表1，俗称“知三求三”．

表1 解三角形

先练习后归纳，学生的学习状态是主动的.学生首先对问题进行归类和识别，联想可能的思路和方法，然后形成初步的想法并按常规的步骤完成．由于这些小题是教师精心选择的，每题仅含一个至多两个基本知识点，一组题又包涵了本节课的所有知识点，因此当学生练习后，“知识点归纳”的事已悄然进行．必要时教师可通过追问，突出本节课的难点，如正弦定理解三角形时如何判定解的个数．

1.1.2 例题选讲

例1已知△ABC的内角A，B，C的对边分别为a，b，c，且2cosC(acosB+bcosA)=c．

1)求C；

3分后，学生基本做完了，教师归纳学生的方法：1)用正弦定理将边化为角，即a，b，c分别换成2RsinA，2RsinB，2RsinC；2)用余弦定理将角化为边，即cosB，cosA用余弦定理代入(也有学生说射影定理的)．学生总结：解三角形的核心方法是边角互化．

师：那能求出什么呢？

生3：能求c的取值范围．

变式1若a+b=5，求c的最值．

“求最值”比“求取值范围”逻辑严谨性弱，尽管变量或图形的变化是连续的；另外，“求c的最值”也可转化为“求三角形周长的最值”．学生编题，教师要把握好“度”．

从确定性问题“知三求三”到不确定性问题，如已知一边和该边对角或已知一角和该角两边的关系，这样的三角形是不确定的，在不确定性问题中我们可以提出“求范围”问题．为什么在解三角形中会有“求范围”问题？怎样提(编)出“求范围”问题？这是笔者本节课的教学起点．

1.2 有选择——以寻找思路为核心

将全班学生分组，前3组学生每组一个变式，第4组任选．

第一组汇报：由余弦定理得

c2=a2+b2-ab=(a+b)2-3ab=

c2=a2+b2-6≥2ab-6=6，

第三组汇报：由余弦定理得

从而

第四组补充说明变式1也可以使用基本不等式求最值．教师总结“求三角形中的范围问题”的方法：二次函数法、基本不等式法．

师：我们回到表1．在已知两边一角或两角一边类型中，条件中减去一条边或减去一个角，三角形就不能确定了，此时可以改求边长、周长或面积的最值，如表2．

表2 解三角形

已知一边及所对角，用余弦定理列式找关系，能够提出的问题都与两个正数的“和”“积”相关．与“和”相关的提出求周长的最值问题，与“积”相关的提出求面积最值问题，或者编拟上述问题的“逆”问题.在变来变去中让学生感悟如何提出问题，并摸清这一类问题的规律．

1.3 有优化——多元表征简化思路

师：在“已知三边求三角”类型中，请同学们作同样的思考．

生4：已知两边，求第三边长的取值范围．

刚说完，下面就众口一词“太简单了”．提出求面积的问题，评价也是如此．

生5：已知一边的长及另外两边的比值，求面积的最小值．

师：请同学们完成下面的高考题．

巡视发现，受思维定势影响，学生基本采用“函数法”，即选定一边a为自变量，将面积表示成a的函数．设BC=a，则

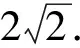
生6：定点C的轨迹是阿波罗尼斯圆，可以用解析几何方法解决．

全班恍然大悟，纷纷改用解析法．待全班做完后，教师及时总结方法并追问．

师：生5编出高考题了，了不起！其他同学有没有想法？

生7：已知一边的长及另外两边的和，求三角形面积的最小值．

师：这是什么轨迹？

生(众)：椭圆．

生8：已知一边的长及另外两边的差，求三角形面积的最小值．

生(众)：双曲线．

师：已知一边的长及另外两边的积，这样的轨迹叫卡西尼卵形线．在这些已知背景下，由于三角形不能确定，我们可以提出求面积、周长等最值问题．由于我们对圆、椭圆、双曲线等轨迹比较熟悉，这类问题的求解用解析法较好，先摸清图形，再判断最值．总结如表3，即在表2中添加一行，并于前面添加行同色同字体．

表3 解三角形

如何提出有价值的问题？从“减少已知边”的角度来看，生4的想法非常自然，只是思维价值不大．多元联系表征理论认为，不同的表征将导致不同的思维方式和不同的学习效果，因此在数学学习过程中强调多层次、多角度选取表征，这样既有助于学生提出问题(由阿波罗尼斯圆联想到两边之比，由椭圆联想到两边之和等)，也能优化解题方法，利用图形的意义直接找到相关的最值．

师：老师的“研究套路”有可能被你们猜着了，下面要干什么？

生9：在“已知三角求三边”类型中编制取值范围问题．

生10：已知两个角，求……

话音未落，全班哑然失笑，该生自己也不好意思起来．

生11：已知角B，即另外两角的和A+C为定值，可以设计关于A，C的三角函数式，求这个式子的取值范围．

师：这样的问题也是高考的热点，题目很多．其解法与正弦、余弦定理无关，本节课暂不涉及．

生12：由于边与角的正弦值对应，因此也可以求边长之比．

师：请看下例．

这样，学生驾轻就熟地将表3再添加一行，即已知“一角”，求“另两角的三角函数式或另两边之比的范围”，教师再将这个新表中3次添加的内容罗列在一起，得以下表4．

表4 解三角形

1.4 有反思——形成元认知结构

通过3次变式，完成表4后让学生回顾“在三角形中求取值范围(最值)”所用方法，填在表4中的“方法联想”中，如二次函数法、基本不等式、解析法(求轨迹)、三角函数法等．追问本节课的本源性问题“为什么解三角形中会有取值范围问题”“这类问题的结构类型有哪些”……实际上就是表4所呈现的内容．“你能否在解三角形中编拟出某一类型的数学题”激发了学生的创造热情，学生借助于“搜题”或自编、讨论和研究做到主动回顾反思．

2 教学反思

反思传统数学课堂，学生习惯于接受现成的结论，解决一些已经解决的问题，教学重点是训练解决这些问题的技能与技巧，教解题而不是教怎样解题．笔者坚持的解题教学“四有”主张试图改变这种现状，本课例的侧重点是让学生发现“三角形中的范围问题”，它“是什么”“为什么”及其规律和方法．

2.1 发现更有数学价值

数学家们常说：在数学中，发现问题往往比证明结论更重要．数学教师应该通过数学课堂培养学生的问题意识，这比再多的习题演练都有价值．正如本节课，如果设计成“知识归纳—典型例题—方法总结—巩固练习”型常态复习课，确实未尝不可，但练得再多，都不如让学生明白这些求范围问题是从哪来的，怎么研究它……当学生掌握了在三角形中研究的一般方法后，我们有理由相信，他们也能掌握在其他范围内发现和提出类似的问题，并将研究方法迁移到这类问题上来．因此，“四有”的第一步“有想法”可以前移，教师将自己的想法传导给学生，搭建学生提出问题的平台，培养学生发现和提出问题的能力．

2.2 讲题揭示问题本质

在例1第2)小题中，教师必须与学生一起分析“不确定”的原因以及此时我们能提出什么样的问题，及时总结获得的解题经验(其实是研究方法)，通过类比再设法在其他“确定性”问题中发现问题、提出问题，如例2中的几何背景揭示和例3中边角关系的转化，通过这样的高质量解题活动让学生弄清楚这类问题的源与流，真正学会发现和提出问题的方法，使学生学会思考．章建跃老师常说：讲答案更要讲过程，讲解题更要讲怎样解题，解题训练更要注意思维训练；降低负担，让学生做适量题目就能达到目的，并取得好成绩，这才是真正考验教师的水平．

2.3 “四有”仍需实践完善

有关解题教学的题目需要教师精心选择，一节课或一个单元的解题教学选题一定要将复习的思想方法蕴含其中.本课例中让学生去感悟、去深度变式的前提是教师先“游题海”；其次，讲答案更要讲过程，教师不能代替学生思考，解法让学生选择，有时错误的方法价值更大；再次，好的解法哪里来，教师的作用是导演，可以通过不断地追问，引导学生类比、联想，激发他们的解题热情，培养良好的解题习惯；最后，要求学生养成反思的习惯，通过反思将知识纳入体系，将思想凝练于心，使知识模型化、方法模式化．