教之道在于“度” 学之道在于“悟”*
(福州华侨中学,福建 福州 350004)
1 问题的提出
《普通高中数学课程标准(2017年版)》(以下简称《新课标》)指出了数学学科核心素养包括:数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析.这些数学学科核心素养既相对独立又相互交融,是一个有机的整体[1].数学核心素养的提升是一个循序渐进、细雨润物的系统过程,不是一朝一夕、一蹴而就所能完成的,必须贯彻到高中数学教育教学的始终,贯彻到数学教学的每一节课,贯彻到每一个数学问题的解决过程之中.课堂是阵地,问题是载体,如何通过问题的解决把培养学生的核心素养落实到位,是当今每一位中学数学教师必须面对和思考的问题.
“教之道在于度,学之道在于悟”,这是中学数学教育家章建跃博士对中学数学教学过程中两个最关键问题——“教”与“学”给出的发人深省的忠告,但是回到中学数学课堂教学的实践过程尤其是数学解题教学过程中,教师的教学“失度”以及学生的学习“被误”现象仍屡见不鲜,最直接的后果是自然美丽的中学数学在学生面前呈现得越来越“面目狰狞”,以至于让学生对中学数学产生“恐惧”“无奈”,部分学生丧失对数学学习的兴趣与信心.
下面笔者举例说明.
案例1方法虽多,思想匮乏.

( )
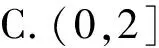
数学考试中的选择题是一类非常重要的题型,要求学生只需选出正确答案,而无需提供具体的解答过程.也正因为这样的特点,使得选择题具有很强的考查学生逻辑思维能力和解决问题能力的功能.

方向1渗透“特殊与一般”与“数形结合”的数学思想.
首先根据已知条件,选取特殊值x=0,y=1,即点(0,1)在圆x2+(y-2)2=1上,从而

亦即
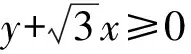

图1 图2
方向2渗透“数形结合”与“化归与转化”的数学思想.
本题是一个“解析几何”问题,文献[2]给出问题的多种构造法解题,但都在寻求与其他相关知识的综合,忙于“弦外之音”, 并没有发现问题的真正本质源于问题本身.由方向1的分析不难发现以下事实:点P(x0,y0)在圆x2+(y-2)2=1上,从而

所以d∈[1,2],故选B.
案例2本质模糊,剑走偏锋.

(2018年5月江苏省南通、扬州等7市高三三检联合考试题第14题)
文献[3]对这道“新颖”的试题进行了详尽分析.当a<0时,显然函数
的图像过第一、二、三象限.当a≥0时,y=ax-1(其中x≤0)的图像仅过第三象限,由题意f(x)=x3-ax+|x-2|(其中x>0)的图像过第一象限和第四象限,等价于函数f(x)=x3-ax+|x-2|(其中x>0)有两个零点,于是给出了解决“函数零点”的3种常用“通法”[3].
分析1(分类讨论)
1)当a<0时,函数f(x)的图像经过3个象限;
2)当0≤a≤1时,……;
3)当1 综上可得a>2. 点评分类、分类、再分类,真的很累! 分析2当a≥0时,数形结合:原问题转化为函数g(x)=x3+|x-2|与h(x)=ax的图像在y轴右侧有两个交点问题,于是对函数g(x)求导数,画三次函数的图像.设切点(x0,y0),解二元三次方程组 得x0=1,a=2,因此a>2. 点评求导、画图、解高次方程组,真的很难! 分析3(分离参数)当a≥0时,在方程x3+|x-2|=ax的两边同除以x,得 点评求分段函数的导数、求分段函数的最值、画分式分段函数的图像,真的很繁! 解本题时,文献[3]先进行调查,让学生大胆说出当时的想法以及思路遇到的障碍.“老师,我直接去绝对值讨论的(函数最值法),好像有点乱,搞晕了,没做完”“我用的数形结合,太紧张了,结果搞反了”“我想到了分参,但也不怎么确定,没敢做,时间也不太够”“我看到这一题时,大脑一片空白,好大一会也没有任何想法”“对对对,我也是,什么想法也想不到,根本没有思路”……[3] 学生想到了做不到,想不到的更做不到,无奈之情一览无余!因此,教师采取了以下对策:1)通性通法的机械性“植入”,费时费力,放手给学生才是有效手段;2)浅层次的一题多练事倍功半,阶梯式的探究方能修得正果[3]. 从上述事实不难发现,一道经过命题专家精心设计、立意新颖、解法多样的填空压轴题,为什么事与愿违,最终变成超高难度、超低效的试题?一所省四星级高中905名学生中只有37人做对,平均分为0.2,难度系数为0.04,令人震惊!文献[3]的作者是一位年富力强的优秀数学教师,不仅有深厚的专业造诣,而且有丰富的教学经验,面对考试结果也不得不喟然长叹:“理想很丰满,现实很骨感”,所教的学生虽然经过“两轮复习”,但是绝大多数学生也未能幸免,仍然是茫然不知所措,望题兴叹,无可奈何……,最后把希望的眼神再次投向教师,于是教师痛定思痛后决定“放手不管”“友情客串”……,以此防止“通性通法‘机械性’植入”,最终提出“浅层次一题多练事倍功半,阶梯式训练方能修得正果”! 在“两轮复习”过程中都没有进行过“阶梯式训练”吗?阶梯式训练就是深层次的训练吗?“放手不管”“友情客串”真的能够防止通性通法的“机械性”植入吗?为什么教师辛辛苦苦地教,学生勤勤恳恳地学,却考出凄凄惨惨的分,令人深思,发人深省!要更好地解决上述问题,笔者认为非常有必要认真学习《新课标》,不断更新教育教学理念,以人为本,以学定教,关注学生的核心素养的提升,不断提高学生解决数学问题的关键能力.在学生还没有学习导数的前提下,教师以文献[3]中的问题为载体,对学生进行核心素养的培养. 教师要引导学生分析问题的本质是什么?由于f(x)=x(x2-a)+|x-2|(其中x>0),显然,无论a是多大的常数,当x取足够大的正数时,函数值一定会大于0,也就是说必过第一象限,这样问题过不过第四象限成为解决问题的关键.图像过第四象限就是函数图像上有点在第四象限,即在函数图像上存在x>0,y<0的点. 通过对问题全面透彻的分析与思考,可以得到解法1: 当x≥2时, 故a>2. 虽然通过“直观感知、数学抽象、数据分析、数学建模、逻辑推理和数学运算”,用精准的数学语言给出问题的正确解答,但是数学核心素养的提高不能停留在一般层次,而是要有不断提高的理念和意识,要从不同侧面对问题的教育价值进行充分提炼.对问题再次进行思考,着重学生“逻辑推理”和“数学运算”这两个数学核心素养提升的侧面考量,选择不同的运算途径,得到解法2: 于是当0≤a≤2时,对任意的x>0,f(x)≥0恒成立,即此时图像不过第四象限,若要使函数图像经过第一象限和第四象限,则a>2. 点评从上述的分析探究过程不难发现,例2的数学本质是分段函数与不等式的关系问题,并不是真正的“函数零点个数”问题.解决函数零点问题是学生应该掌握的通性通法问题,通性通法固然重要,但是通性通法并不简单等同于某种“套路”,见题就套,盲目乱套,这样不但不能将问题“套牢”,往往是自己被问题“套牢”.真正的通性通法就是要具有数学的核心素养和关键能力,然而核心素养和关键能力绝不是某种单一的训练模式所能够培养和提高的,面对数学问题尤其是新问题,教师每每都是好心为学生提供这样或那样的“阶梯”进行若干“铺垫”,这种“甘为人梯”的精神虽然可嘉,但一旦学生离开课堂这块特殊的“阵地”,就会遇到诸多的无奈,茫然不知所措,不利于学生的终身发展. 作为新课程改革时代的教师,“教什么”和“怎么教”是教师需要面对和思考的问题,教师辛辛苦苦地教,学生勤勤恳恳地学,为什么会收效甚微?虽然原因众多,但最重要的是教师在数学问题的解决过程中有没有关注学生思维的发展、有没有挖掘问题的本质、有没有从数学核心素养的要求出发从数学问题的解决过程中汲取和提炼养分、有没有提升学生的核心素养、有没有提高学生的关键能力……只有把关注学生核心素养、提高关键能力作为教学常态,才能使教师和学生双双从辛苦和痛苦中解脱出来,返璞归真,浑然天成.

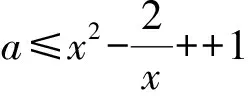
2 问题的启示

