2019年全国数学高考卷Ⅰ理科第18题的评析*

(临泉田家炳实验中学,安徽 临泉 236400)(临泉田家炳实验中学,安徽 临泉 236400)(临泉县第二中学,安徽 临泉 236400)

虽然一年一度的高考已落下帷幕，但是围绕着高考的热议并未随之消退.伴随着《普通高中数学课程标准(2017年版)》的出台，2019年的高考试题继续担负着从“能力立意”向“素养导向”转变的重任[1].回望全国数学高考卷Ⅰ理科试题，“维纳斯”、导数、解析几何以及概率统计压轴题等，曾引无数专家、一线教师以及数学爱好者的竞相研究.而作为较为传统的立体几何解答题，似乎备受“冷落”.然而，在笔者看来，它既保持“传统”，又散发着独特的“韵味”.

图1

1 试题呈现

例1如图1，直四棱柱ABCD-A1B1C1D1的底面是菱形，AA1=4，AB=2，∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.

1)证明：MN∥平面C1DE；

2)求二面角A-MA1-N的正弦值.

(2019年全国数学高考卷Ⅰ理科试题第18题)

纵观近几年全国数学高考卷Ⅰ理科立体几何试题，例1在保持题型、分值以及问题设置不变的基础上，突出“起点低、入口宽、方法灵活”的特点,凸显空间向量在解决立体几何问题中的工具性作用，践行了“人人都能获得良好的数学教育，不同的人在数学上得到不同的发展”的理念[2].

例1设置了两个小问题，考查的知识涉及线线、线面、面面的平行与垂直以及直棱柱、菱形、二面角等，综合考查学生的空间想象、逻辑推理以及运算求解能力.其中第1)小题考查线面平行的判定，可以借助空间向量，也可以转化为线线平行或面面平行证明.下面主要分析第2)小题.

2 一题多解

2.1 整体策略分析

从整体上讲，解决第2)小题有两种思路.思路1是向量法，借助于空间直角坐标系，把几何要素坐标化，即把几何问题转化为代数运算处理.这种思路的优点是利用空间向量的特性(自由向量)，避免了用综合几何法作二面角的平面角所带来的不便.思路2是综合几何法，以二面角的平面角的概念为依据，经历解决问题的3个步骤:1)根据几何图形的特征作出平面角；2)说明这个平面角是所要求的二面角的平面角；3)根据几何要素计算二面角的平面角(或三角函数值).在这3个步骤中，步骤1)是后面两步的前提，是解题的关键，它需要学生具备很强的“识图”“绘图”能力.

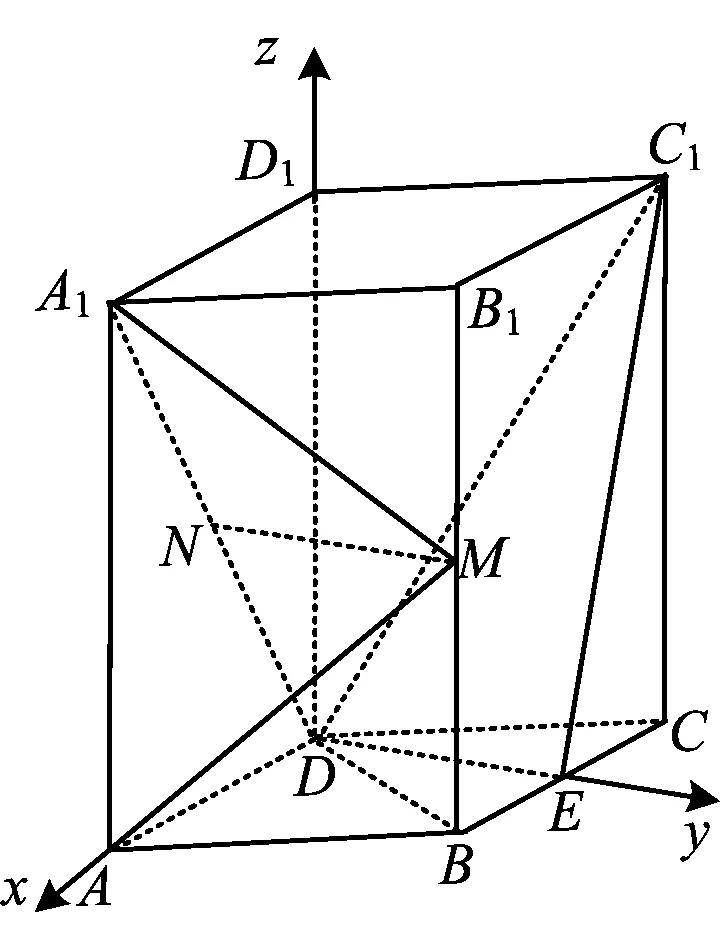
图2

2.2 解法展示

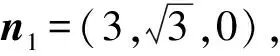
则

评注此解法的关键是根据几何体的结构特征，建立合适的空间直角坐标系.由于此几何体是直四棱柱，且底面是菱形，因此有不同的建系方法.除了图2的建系方法，还可以“分别以AC,BD所在直线为x,y轴、以它们的交点O为坐标原点建系”或“分别以BC,ED所在直线为x,y轴、以E为坐标原点建系”等.

以下5种解法都是综合几何法.

图3

解法2如图3，过点N作NO⊥A1M于点O，再过点O作OP⊥A1M交AA1于点P.联结PN，则∠PON是二面角A-MA1-N的平面角.

联结ME，B1C.因为M,E分别是BB1,BC的中点，所以

ME

又因为A1DB1C，且N是A1D的中点，所以

MEND，

故四边形DEMN是平行四边形，从而MNDE.由解法1知，则DE⊥平面ADD1A1，于是MN⊥平面ADD1A1，进而

在Rt△A1MN中,

从而

因为△ABM与△A1B1M均是直角边长为2的等腰直角三角形，所以

从而

OP∥AM,OP⊥A1M,

于是

在△A1PN中,

进而

故

评注此解法利用二面角的平面角的概念，先在一个半平面内向二面角的棱作垂线，然后在另一个半平面内过棱上的垂足作垂线，进而构造三角形，通过解三角形求出结果.采用此解法的前提是找不到二面角的两个面的垂线，无法直接构造包含二面角的平面角的直角三角形，因此这种方法虽然思路简单，但是过程繁琐.其实，进一步探究可得PN⊥平面A1MN.

图4

解法3如图4，过点A作AO⊥A1D于点O，联结OM.由解法2知，DE⊥平面ADD1A1，从而平面DEMA1⊥平面ADD1A1.因为平面DEMA1∩平面ADD1A1=A1D，所以AO⊥平面DEMA1.又因为AM⊥A1M，所以∠AMO是二面角A-MA1-N的平面角.

评注此解法的难点是确定点A在平面DEMA1内投影的位置.要确定它的准确位置，要先判断平面DEMA1⊥平面ADD1A1，然后根据面面垂直的性质定理解决问题.当然，若不能确定点A在平面DEMA1内投影的位置，则可通过VM-AA1D=VA-MA1D直接求出点A到平面DEMA1垂线段的长度，进而求出结果.

解法4如图5，在平面ABCD中，作AO⊥AB交ED的延长线于点O，联结OM，则OM在平面DEMA1内.因为平面ABB1A1⊥平面ABCD，所以AO⊥平面ABB1A1.又因为AM⊥A1M，所以∠AMO是二面角A-MA1-N的平面角.

由解法2知，DE⊥AD.在Rt△ADO中，

AD=2, ∠DAO=90°-∠BAD=30°,

从而

在Rt△OAM中,

于是

评注此解法的难点是：1)过点A作平面ABB1A1的垂线AO,AO与平面DEMA1的交点在哪；2)如何求出线段AO的长度.这需要对空间几何体的位置关系以及数量关系有清晰的认识.

图5 图6

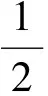
于是

在Rt△DPO中，

故

评注此解法是建立在AB,A1M,DE相交于一点的基础上.通过DP⊥平面ABB1A1，确定点P在直线A1F上的投影O，得到平面角.然后利用平行线的性质，得到线段的长度，从而求出结果.

图7

解法6如图7，由解法5知A1M,AB,DE相交于点F，并且点B是AF的中点.在平面ABCD中，作EP⊥AF于点P，再过点P作PO⊥A1F于点O，联结OE，易知∠POE是二面角A-MA1-N的平面角.

在Rt△EPB中，EB=1，∠EBP=60°,则

因为AM⊥A1M，所以AM∥PO，从而

于是

在Rt△EPO中,

故

评注此解法与解法5类似，借助点E构造二面角的平面角处理.

2.3 解法对比

以上6种解法，既有区别也有联系.区别在于解法1是向量法，突出向量在解几何问题中的作用;其他5种解法是综合几何法，重在利用几何方法解决几何问题.而这5种方法的内部也存在区别:从作图的角度看，这5种解法分别从不同的点(点N,A,D,E)出发，作二面角的棱的垂线，或作二面角的面的垂线，进而构造二面角的平面角.从解法的难易看，解法2思路简单，但运算复杂，书写繁琐，而其他的4种解法思维量大、运算简单、书写方便.

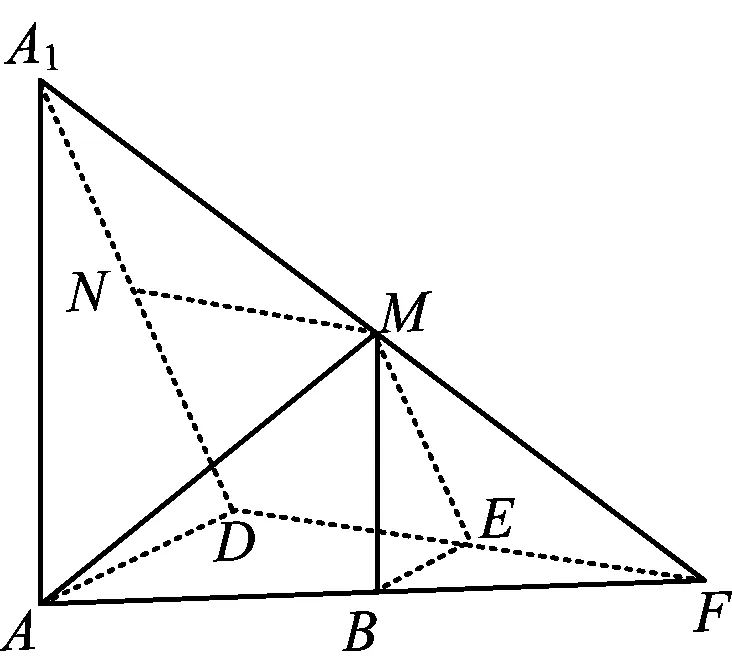
图8

它们的联系在于从不同的角度解决同一问题.观察图6，分别延长A1M,AB,DE相交于一点F，得到一个三棱锥A1-AFD,并且点B,M,E分别是所在棱的中点，平面A1DF⊥平面A1AD，平面A1AF⊥平面AFD，平面A1AD⊥平面AFD.把这个三棱锥分离出来(如图8)，不难发现：求二面角A-MA1-N的正弦值的实质就是求三棱锥A1-AFD的两个侧面A1AF,A1DF所构成的二面角的正弦值.接下来只需要从不同的角度作二面角的平面角即可解决问题.其中，解法2、解法3都是作平面A1DF的垂线，只是所过的点(即点N,A)不同而已.解法4～6则是作平面A1AF的垂线，所过的点分别是A,D,E，再结合三垂线定理，得到二面角的平面角，然后通过几何知识求得结果.

3 一题多变

在例1的基础上，通过变换不同的载体，比如把“直四棱柱”换成“正方体”“长方体”“一般棱柱”或者变换已知条件，比如点M的位置等，可得到不同的题目：

例2如图9，正方体ABCD-A1B1C1D1的棱长为4，M,N分别是BB1,A1D的中点,求二面角A-MA1-N的正弦值.

例3如图10，在长方体ABCD-A1B1C1D1中，AA1=4，AB=AD=2,M,N分别是BB1,A1D的中点,求二面角A-MA1-N的正弦值.

例4如图11，四棱锥ABCD-A1B1C1D1的底面是菱形，AA1=4，AB=2，∠BAD=∠BAA1=∠DAA1=60°,求二面角A-MA1-N的正弦值.

例5如图12，直四棱柱ABCD-A1B1C1D1的底面是菱形，AA1=4，AB=2，∠BAD=60°,E,M,N分别是AD,CC1,A1E的中点,求二面角A-MA1-N的正弦值.

图12 图13

例6如图13，在正四棱台ABCD-A1B1C1D1中，AB=4,A1B1=2，AA1=4，M,N分别是BB1,A1D的中点,求二面角A-MA1-N的正弦值.

4 思考

4.1 抓住试题的本质

面对同一个问题，从不同的角度分析，能够得到不同的解法.对于这些解法，教师不能仅仅满足于展示，而应深入研究这些解法的区别何在、联系在哪里，同时要善于透过不同解法的表面，挖掘试题的内涵与本质.

比如例1的第2)小题求二面角A-MA1-N的正弦值，我们从不同位置(点N,A,D,E)出发，构造二面角的面的垂线，进而作出平面角.其中解法2与解法3是作平面A1DF的垂线，解法4～6则是作平面A1AF的垂线，其过程大同小异，繁简有别.然而，拨开这些解法的“面纱”，不难看出问题的本质是求三棱锥A1-AFD的两个侧面A1AF,A1DF所构成的二面角的正弦值(如图8)，只是看的角度不同而已.只要把握住这一点，也就掌控了解决问题的“钥匙”，接下来只需“开锁”就行了.

4.2 挖掘试题的教育价值

众所周知，高考试题具有选拔、诊断和导向功能.不仅如此，它还具有培养学生的数学思维能力的价值.比如，一题多解能够培育学生思维的敏捷性与发散性，一题多变可以培育学生思维的深刻性与灵活性.因此，对试题价值的开发既要注重一题多解，也要结合试题的特征，注重多题一解以及一题多变.

对于例1，教师可以实施一题多解教学，让学生充分思考、交流，得到不同的解法，然后让学生比较这些解法的区别与联系，找到它们隐藏的共性，进而归纳解决这类问题的合理的解法；也可开展变式教学，除了教师改编试题，也可尝试让学生改编试题，比如改变试题的条件或结论，让学生能从一个题看到一类题，既能看到树木，也能看到森林.例1可以改变载体，从一般的直四棱柱到正方体、长方体、斜四棱柱甚至正四棱台，从而在新的问题下把学生已有的认知经验重新加以组合，达到“既换汤，又换药，甚至换碗”的效果.当然，对例1的变式，笔者仅仅改变载体，其实还可以改变其他条件以及结论或者条件与结论都改变，使得试题的内涵更加丰富多彩.