基于二维数学模型的淤地坝溃坝模拟研究

张 杨 曹 伟

（1 山西省水土保持生态环境建设中心 2 山西省水资源管理中心）

1 研究区及淤地坝概况

利贞寨淤地坝地处介休市西北义棠镇利贞寨村，坝址坐标：东经111°48′27″，北纬37°01′33″，距市区约20 km。坝控流域属黄河水系的汾河一级支流，控制面积3.05 km2。该流域主沟道长约3.3 km，支毛沟共16 条，沟壑密度2.7 km/km2，沟道平均比降2.9%。据介休市气象站观测资料，年均降水量465 mm，汛期高度集中，7-9月份降雨量占到年降水量的72.7%；最大24 h 暴雨均值60 mm，易形成短历时洪水，并含有大量泥沙。

利贞寨淤地坝由坝体和放水建筑物（卧管、涵洞）“两大件”组成，筑坝材料为黄土，坝型为均质碾压土坝。坝高17.3 m，坝长114 m，库容大约在50-100 万m3之间，从坝高和库容来看属大（2）型骨干淤地坝。设计洪水标准为20 a 一遇，校核洪水标准为200 a 一遇，设计淤积年限为15 a。由于当地暴雨集中，淤地坝设计洪水标准较低，极易遭遇超标准洪水。当遭遇到超标准洪水时，因未设置溢洪道放水建筑物，该淤地坝往往会发生洪水漫顶，甚至导致溃决[1]。

2 溃坝流量过程线计算

据经验，土石坝的溃决方式一般为逐渐溃决。本次研究主要考虑两种溃坝方式：一是校核洪水位下的逐渐溃坝；二是特殊情况下（地震或战争）的瞬间全溃。

溃口流量计算，采用土石坝溃坝统一公式[2]。

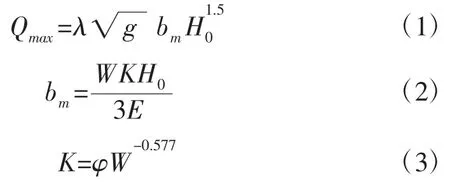
式中：Qmax——溃坝峰顶流量，m3/s；

H0——溃坝前上游水深，m；

g——重力加速度，9.8 m/s2；

λ——流量参数；

W——坝内洪水量，万m3；

bm——口门宽度，m；

K——冲刷系数；

φ——土质系数；

E——坝体横断面积，m2。

式中：σ、m、f 分别为沉溺系数、断面形状参数和堰高比；n2、n4、n6分别为指数；e 为堰宽比。

峰前流量过程线计算公式：

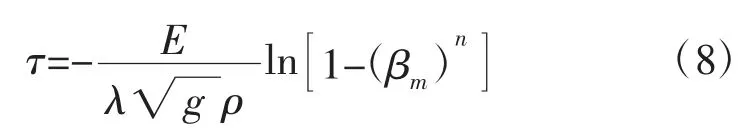
峰后流量过程线计算公式：

式中：q——峰前流量，m3/s；

Qm——峰前库区洪水量，万m3；

βm——溃坝处最大水深比；

H——峰前坝前水深，m；

W总——总库容，万m3；

ρ——洪水平均体积含砂量，%；

n——库容指数，该指数值一般为2-2.5，本文取n=2.3；

τ——时间，s；

图1 逐渐溃坝流量过程线

由于溃口不断增大，流量也在逐渐增大，当溃坝147 s 左右时，流量达到峰值，而后开始逐渐减少；校核洪水位下逐渐溃坝最大下泄流量为622.87 m3/s，总历时1 860 s 左右。图2所示的为瞬间淤地坝全溃情况，溃坝流量过程在开始时达到峰值，随着大量洪水下泄，坝内水位不断降低，溃坝流量随时间延长也在逐渐减少；瞬间全溃的峰值流量，最大可达到2 218.23 m3/s，历时270 s 左右。

3 数学模型的构建及模拟

3.1 模型原理

水动力数学模型的基本控制方程是二维浅水方程[3]。

（1）连续方程：

（2）运动方程：

W′总——峰后洪水总量，万m3；

H′0——峰后坝前洪水水深，m。

放空时间按下式计算，近似n=2.5 时：

式中：D2（ξ1）查表为2.495。

根据相应的n 值，查《溃坝水力学》专著中的表3-8 至3-13 可得，再根据以上公式，即可求出峰后流量过程线。

图1所示的为淤地坝逐渐溃决模拟情况，开始

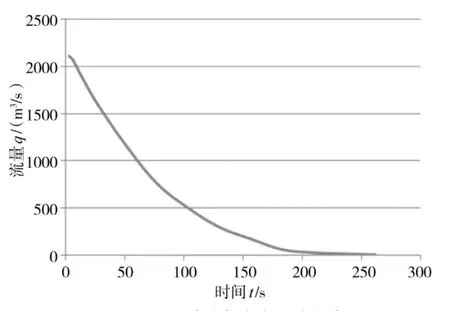
图2 瞬时全溃流量过程线

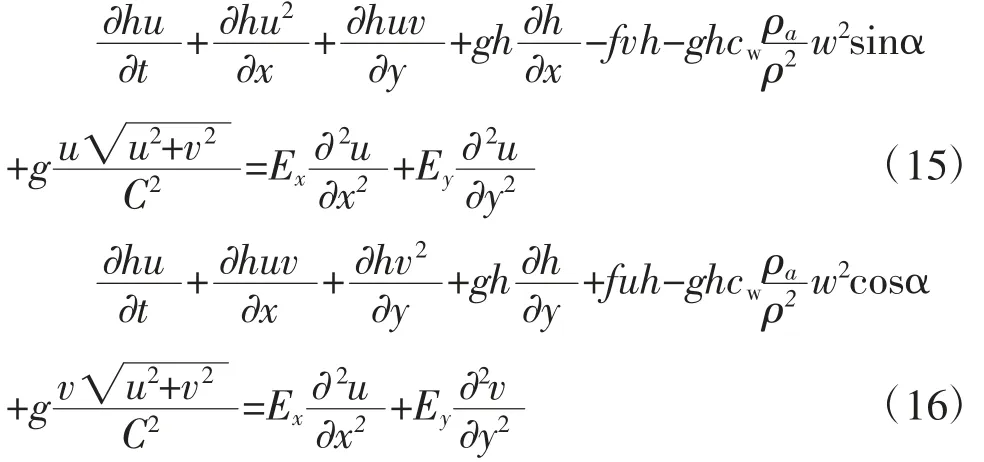
式中：h——水深，m；

x、y——横轴和纵轴坐标；

t——时间，s；

g——重力加速度常数；

u、v——x 和y 方向沿垂线平均流速，m/s；

f——柯氏力系数；

ρ——洪水密度，kg/m3；

ρa——空气密度，kg/m3；

cw——风的摩阻系数；

w——实时风速，m/s；

Ex、Ey——x 和y 方向的涡粘系数；

在控制方程的求解过程中，使用有限体积法进行离散，采用三角形网格；时间积分采用显式欧拉格式；计算中采用干湿网格方法对浅滩进行考虑。

3.2 模型构建

模型构建的基本内容包括：地形数据导入及地形制作、地形网格的划分、设置初始条件及边界条件等。另外，根据实际情况，在本次溃坝洪水演进模型建立过程中，不考虑风、浪、温度、盐度等因素的影响。

图3 网格划分图

利贞寨淤地坝下游地区的地形数据，以美国SRTM（Shuttle Radar Topography Mission）数据库中下载的数字高程为基础，确定大致行洪范围，划定模型边界，并对计算区域用不规则三角形剖分；然后对散点图进行内插，得到模拟区域的地形文件。模型网格划分图如图3所示，共计13 925 个三角形网格。

建立模型时，选定利贞寨淤地坝坝址处为入流边界，入流边界条件为溃坝流量过程，下游则为自由出流的开边界。模型模拟初始时，下游模拟区域无水流，软件中的初始条件水位设置为模拟区域中地面高程最低值。设置网格计算时间步长10 s，总计算步数为360 s，即模拟1 h。洪水演进过程中，淤地坝下游模拟区域中的水位会发生涨落，因而存在着动边界，需要在设置中添加干湿水深，以保证模型计算连续不中断。其中：干水深设为0.005 m，即计算过程中若某一区域水深小于干水深值，则该区域不参加计算；湿水深为0.1 m，即计算过程中某一区域水深大于0.1 m，则该区参与计算。

3.3 模拟结果

为了直观表现坝下游区的水深随时间的变化过程，在坝下游淹没区选取了3 个特征点T1、T2、T3（分别距离淤地坝1.07 km、2.89 km 和4.32 km）。由图4可以看出，在逐渐溃坝情况下，距离坝最近的T1点洪水到达时间较短，最大水深约4.2 m；随着下游地区与坝距离变远，洪水到达时间变长，淹没水深变小，急骤性洪水损害逐级减弱。由图5可以看出，在瞬时溃坝情况下，距离坝最近的T1点洪水到达时间较逐渐溃坝情况下有所提前，但是最大水深变浅约为3.4 m，其他情况与逐渐溃坝较为接近。

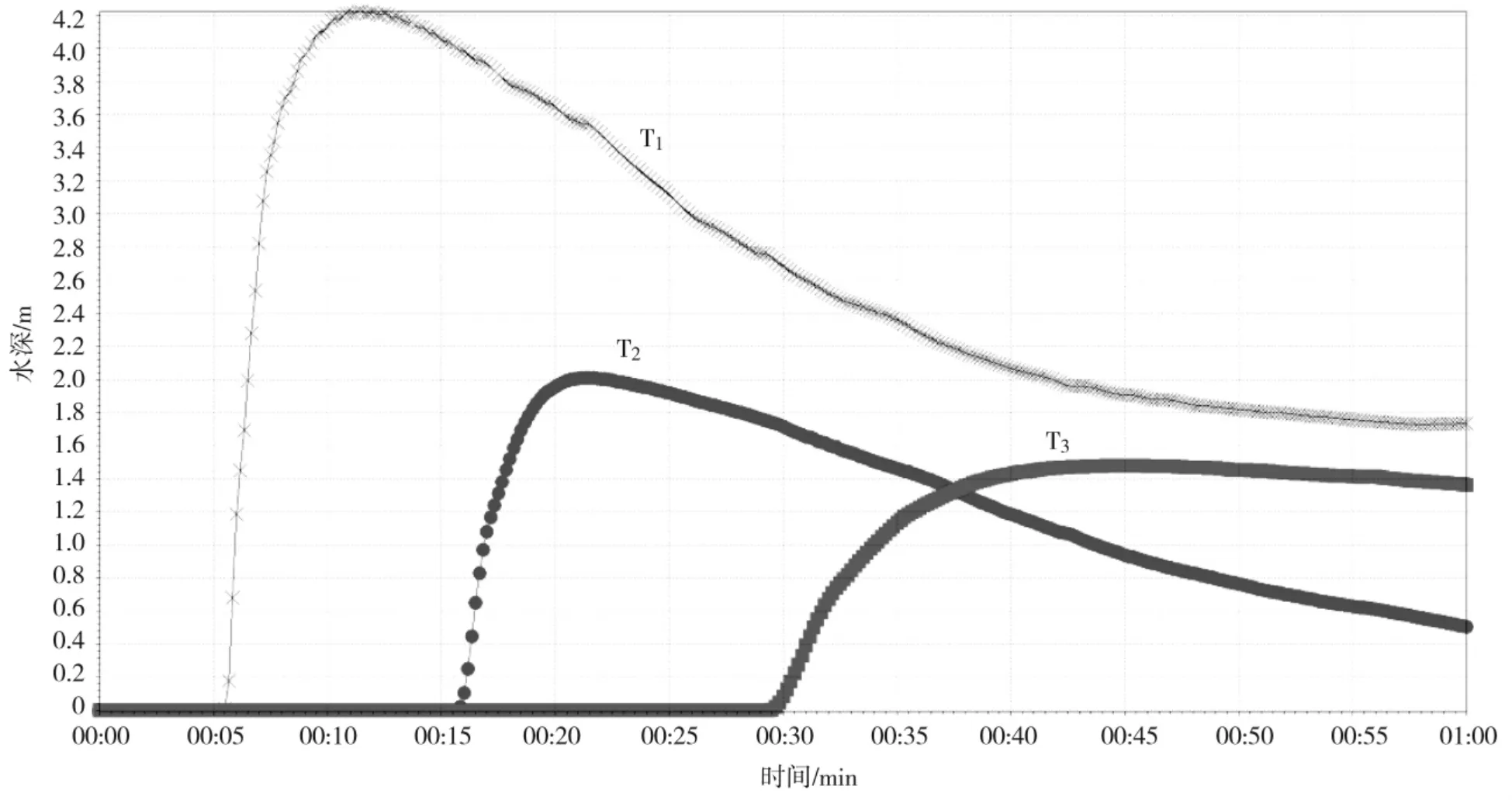
图4 逐渐溃坝特征点水深过程线

图5 瞬时溃坝特征点水深过程线

通过统计模型计算的输出结果，对比两种溃坝工况下溃坝后10 min、30 min、1 h 的淹没范围，逐渐溃坝下对应的淹没面积分别为0.21 km2、1.12 km2和1.81 km2，瞬时全溃下对应的淹没面积分别为0.21 km2、0.61 km2和0.91 km2。

3.4 模型验证

本文采用水量平衡法来验证模型合理性，验证过程如下：

根据计算出的溃口流量过程，算出溃坝后不同固定时间内下泄的水量，然后同模拟下游淹没的水量进行比较，求出两者误差。验证结果见表1。根据水量验证结果可知，溃口流量过程线计算的水量与模拟结果中的淹没地区水量，最大相对误差为3.27%，各时间段误差均在允许范围之内。由此可见，上述溃坝模型能较好地反应溃坝洪水演进特性。

表1 水量平衡验证模型结果表

4 结论

（1）以利贞寨淤地坝为研究对象，计算出两种不同溃坝情况下的溃坝流量过程线，并利用二维水动力学模型对淤地坝溃坝后的洪水演进过程进行模拟，模拟出了溃坝后不同时间段洪水的淹没范围、水深等结果。经验证表明，该模型具有较高精度，能够较好地应用于淤地坝溃坝洪水演进模拟。

（2）目前，山西全省共建有淤地坝4 万余座，数量多且建设时设计洪水标准偏低、配套工程不完善，若运行后如果疏于管理，将会导致溃坝风险。淤地坝一旦溃决，将对下游人民群众的生命财产安全造成不可估量的损失。利用数学模型模拟溃坝后洪水的演进，可以科学评估溃坝的影响范围及程度，为淤地坝的防洪减灾提供技术支撑，对我省淤地坝安全运行具有重要意义。