关于Kaczmarz算法的一个注记

梁茂林，代丽芳

（天水师范学院 数学与统计学院，甘肃 天水741001）

1 预备知识

线性方程组在工程和科学计算中扮演着重要角色，比如许多偏微分方程离散化后往往可以表示为此种形式[1,2].随着人们对运算精度要求的不断提高，网格剖分越来越精细，所导出的线性方程组往往是大规模稀疏的，如果运用直接方法求解此类问题是不可行的，而迭代法由于其存储量和运算速度的优势受到人们的青睐，从而涌现出了求解线性方程组的许多迭代算法，一些经典算法见文献[2-6]. 值得一提的是，Kaczmarz 算法是求解线性方程组的一类重要方法[5]，有关该算法进一步的研究及其推广非常深入，如文献[6-8]等，但是少有关于经典Kaczmarz 算法原理方面的讨论. 本文利用向量内积的性质和矩阵广义逆的有关理论，分别从几何和矩阵论角度研究了Kaczmarz 算法的迭代原理.

给定线性方程组

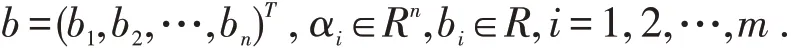
经典的Kaczmarz 算法的基本思想是，对于任意给定的初值x(0)，将其投影到线性方程组(1)中的第一个方程α1Tx=b1的解集合中，得到x(1)；然后将x(1)投影到方程(1)中的第二个方程α2Tx=b2，得到x(2)；如此循环直到得到满意的结果. 对于i ∈{1,2,…,m}，Kaczmarz算法的第k 步迭代格式如下：这里符号＜·,·＞表示两个向量的内积，‖ ‖· 表示向量的2-范数.

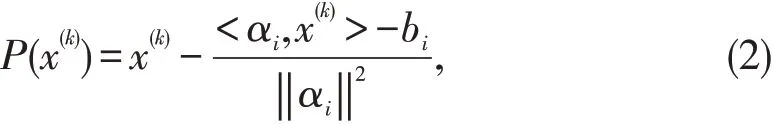
2 主要结果

2.1 利用向量内积的性质

对给定α ∈Rn,d ∈R，根据Kaczmarz 算法的迭代步(2)，我们只需要考虑如下问题：将任意点z ∈Rn投影到超平面αTx=d 内，记其投影点为P(z).

事实上,由超平面方程αTx=d 可得，

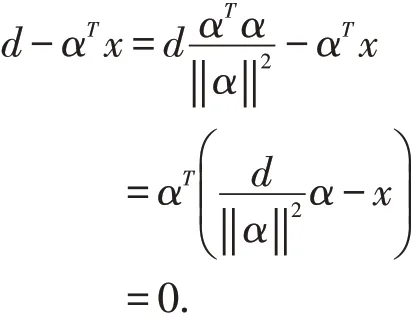
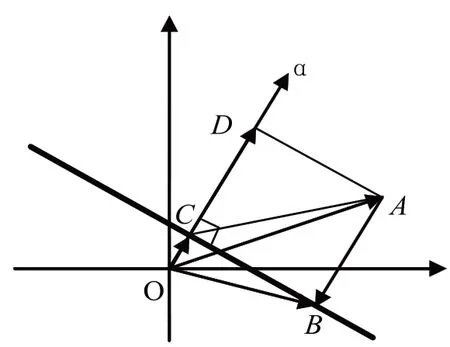
图1 点Z在超平面内的投影示意图

在ΔABC 中，依据向量的加法法则可得

|A→B |=|C →D |=|C →A |cos∠DC .

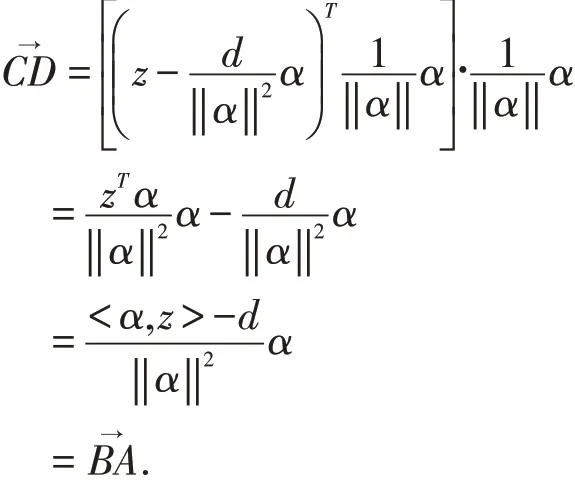
结合式(3)可得点z 在超平面αTx=d 上的投影P(z)为

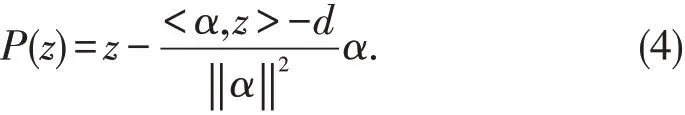
由式(4)可得Kaczmarz算法的迭代格式(2).

2.2 利用最小二乘理论

对于上述给定的α ∈Rn,d ∈R ，将任意点z ∈Rn投影到超平面αTx=d 的投影等价于逼近问题

的极小范数解.根据矩阵广义逆的性质知[9]，非零向量α ∈Rn的 广 义 逆 表 达 式 为，则 方 程αTy=d 的一般解为

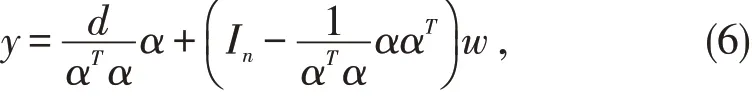
其中w ∈Rn为任意向量，In表示n 阶单位矩阵.将式(6)代入式(5)，则有

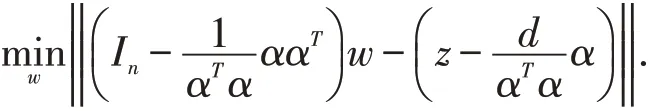
这是一个以w 为未知量的经典最小二乘问题.根据广义逆矩阵相关理论可知，其极小范数最小二乘解，即为点z 在超平面αTx=d 上的投影P(z)，且可以表示为

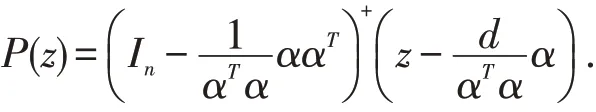
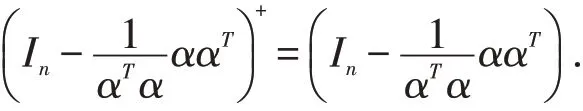
从而，上式可以简化为

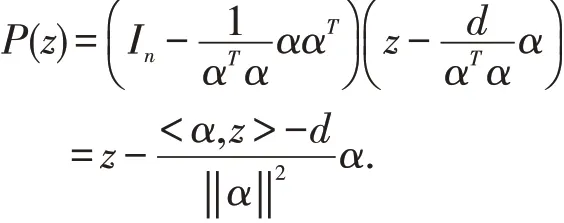
显然，得到了与(4)式中相同的表达式.