基于新矩阵变量下的测地线方程

王 根

（浙江师范大学 数学与计算机科学学院，浙江 金华 432001）

平直时空是用欧式几何描述的，两点间的最短线直线占有重要地位。弯曲时空中一般不存在直线，但是，两点间会有最短线，统称测地线。测地线在黎曼几何中的作用，相当于直线在欧式几何中的作用。 数学上测地线可视作直线在弯曲空间中的推广；曲面上非直线的曲线是测地线的充分必要条件是除了曲率为零的点以外，曲线的主法线重合于曲面的法线[1，3-5，7-8]。目前，关于测地线方程的具体求解还存在一定的难度性，具体的解还依赖于具体的坐标系的选取[2，6，9]，这给测地线方程的研究带来了复杂度。

定义[1]设Y是沿曲线γ∶(a，b)→M定义的向量场，若由仿射联络∇给出∇γ′ Y=0，则称Y沿曲线γ平行，特别，当γ′沿自身曲线γ平行时 ，即 ∇γ′ γ′=0，则称γ为M上的测地线。显然，Y沿曲线γ平行的局部坐标表示为

γ为M上测地线的充要条件为

本文使用新定义的变量考虑了如下测地线方程的微分动力系统性质即一阶常微分方程组[3]，

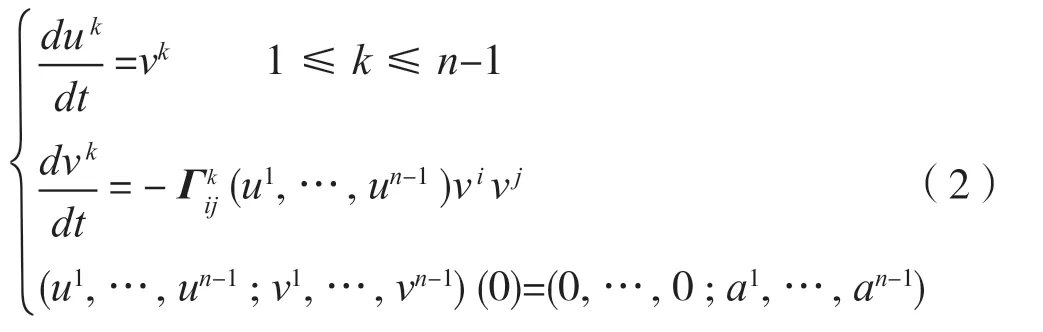
1 记号与引理

引理1[3]在一个局部坐标系(U，ui)下，联络∇∶是可以任意确定的，在自然标架场的运动规律：

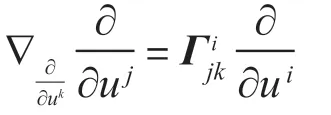
因此Riemann流形M上的向量场的协变导数为

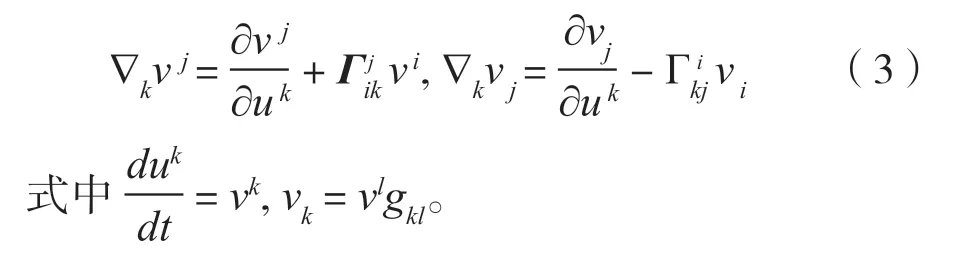
引理2[3]设M为Rn中n-1维C2正则超曲面，若M上的一条C2曲线C满足

则称该曲线为一条测地线，其中u=(u1，…，un-1)为M上的参数，x(u)=x(u1，…，un-1)为M的参数表示，t为曲线C的参数。

证参见文献[3]中第2章第8小节定义2.8.3。

引理3[4]

1）n维C∞流形M的切丛TM上的线性联络∇满足挠张量T=0 ⇔对任意局部坐标系

2）∇ 满足：(a)Z(X，Y)=〈∇Z X,Y〉+〈X,∇Z Y〉，∀X,Y,Z∈C∞(TM)；(b)∇g=0，(c)对任意局部坐标系平行移动下保持内积不变。

证参见文献[4]中第1章第3小节定义1.3.5。

引理4[6][渐近线性稳定]对于所有的x0都有当且仅当A的所有特征值都有负实部。

证参见文献[6]中第2章定理2.10，p60。

引理5[5]给定齐次常系数线性微分方程组x·=那么

1）若A的特征值的实部都是负的，则它的任意解当t→+∞时都趋于0。

2）若A的特征值的实部都是非正的，且实部为0的特征值都是简单特征值，则它的任意解当t→+∞时都保持有界。

3）若A的特征值至少有一个具有正实部，则它至少有一解当t→+∞时趋于无穷。

证参见文献[5]中第5章定理11，p220。

引理6[5][存在唯一性定理]若A(t)是n×n矩阵，f(t)是n为列向量，它们都在区间a≤t≤b上连续，则对于区间a≤t≤b上的任何数t0及任一常数向量η=(η1，…，ηn)T，方程组

存在唯一解φ(t)定义于整个区间a≤t≤b上，且满足初始条件φ(t0)=η。

证参见文献[5]中第5章5.1节定理1，p179-p184。

2 主要结果

定义2设(M，g)是Riemann流形，在一个局部坐标系(U，ui)下，联络∇满足引理1的条件，则定义几何变量为

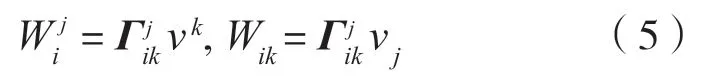
式中vj，vj是切矢场的分量，矩阵

由引理3的性质1得到Wkj=Wjk，因此，协变导数（3）改写为形式Wkj，引理2可以改写为简洁形式k=1，…，n-1。 定义 1 中的（1）写为形式线性形式测地线方程（2）改写为一阶常微分方程组

定理[测地线方程基本解定理]二阶测地线方程（4）成为矩阵初值问题

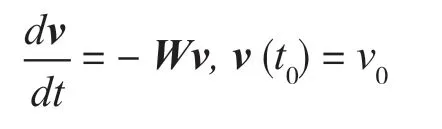
则有唯一的解v(t)=v0e-Wt。

证根据常微分方程组的理论，对于给定的可微速度曲线γ′∶vi=vi(t)，t∈[t0，t′]，以及给定的初值矩阵初值问题有唯一的一组解使得=vi(t0)，由引理6的存在唯一性定理即可得证。

以上定理将测地线方程简化为了线性问题，解的具体形式完全依赖于矩阵W，也就是将测地线问题集中到了对矩阵W的分析与研究，所以只要弄清楚了矩阵W的性质，测地线方程的解与性质也就完全知道了。

事实上，形式上，定理的解可以表示为级数形式

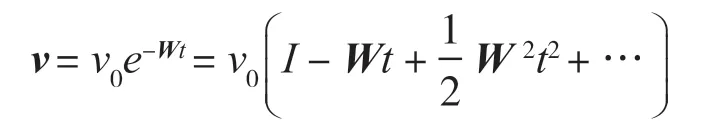
易得常数解v(t0)=v0对应第一项。由易得坐标解为代入级数形式得到

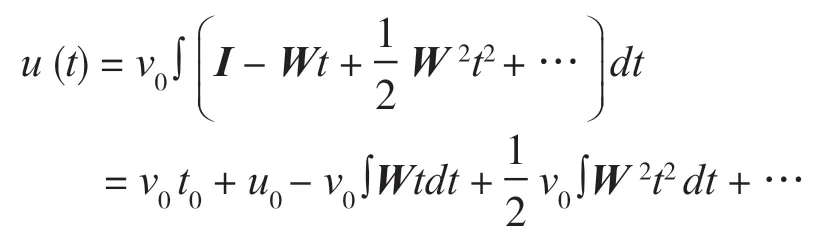
其中初始坐标为u0=u(t0)。以上通过定理间接地得到了测地线方程的坐标解u(t)。很显然地，定理的零解v=0是稳定的，这一点可以很清楚得到。实际上，定理的唯一解具有普遍性，它不随坐标系的选取而改变形式只要测地线方程（4）的形式保持不变。我们记坐标非线性项为

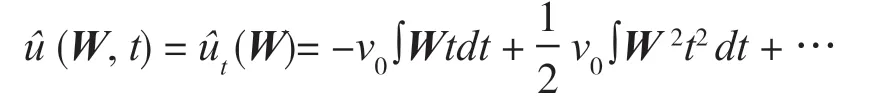
推论设矩阵W的复特征值为λ=w+iq，则定理的解可以写为v=v0e-wt e-iqt，根据引理4与引理5分析可以得到如下结论：

1）若w＞ 0，则它的任意解当t→+∞时都趋于 0，此时是渐近线性稳定。

2）若w都是非负的，且实部为w=0的特征值都是简单特征值，则它的任意解当t→+∞时都保持有界，即v=v0e-iqt。

3）若存在一个w＜ 0，则它至少有一解当t→+∞时趋于无穷。

由一阶测地线方程（6）易得测地线方程的二阶导数如下方程