基于修正共轭梯度算法的设计类App 图像识别算法的研究

张 婷

（福建工程学院 应用技术学院，福建 福州 350001）

伴随移动互联网的快速发展，智能手机App、PC 端网站和平板电脑已成为用户使用数字媒体的重要信息载体。《移动用户需求与行为调研报告》显示，超过90%的移动用户几乎每天都会使用移动社交App，且人均每天在移动媒体上所花费的时间为1.5 h，70% 以上的用户会在空闲时间使用移动端App 应用［1-4］。设计类App（例如堆糖、站酷等）主要以图像搜索为主，因此研究移动端设计类App中图像识别的相关算法是非常有必要的。

本文先将设计类App 中常见的图像特征归纳为颜色、纹理、形状和空间关系等4 类，并构造了4个特征矩阵及以这4 个矩阵为系数矩阵的一类线性矩阵方程［5］。将App 中的图像近似搜索匹配问题转化为求解这类线性矩阵方程是本文研究图像识别算法的关键，如何求解该类矩阵方程是本文研究的重点。修正共轭梯度算法是求解矩阵方程的有效算法［6-7］，本文在此算法的基础上建立求解这类多变量矩阵方程的迭代算法，当方程有解时，根据该算法可以求得此类方程的解，则在已知图库中可以找到匹配的图像；当方程无解时，可以求该方程的最小二乘解，则能在已知图库中找到最相似的图像。该算法的建立，能更好地解决设计类App中图像识别近似匹配的问题。

1 矩阵方程的系数矩阵建立

在设计类App图像识别的过程中，图像信息的获取主要是通过用户在手机前端所选择的某一感兴趣的区域图像进行近似匹配。首先需要将图像信息抽象化，根据图像的颜色特征、纹理特征、形状特征和空间关系特征，分别构造图像的颜色特征矩阵、纹理特征矩阵、形状特征矩阵和空间关系特征矩阵，并分别记为A、B、C、D，获取到的目标区域图像矩阵记为E。其中，A、B、C、D、E均为n阶方阵。

1.1 颜色矩阵构造

颜色矩是一种简单有效的颜色特征表示方法，有一阶矩（均值，mean）、二阶矩（方差，variance）和三阶矩（斜度，skewness）等。由于颜色信息主要分布于低阶矩中，所以用一阶矩、二阶矩和三阶矩足以表达图像的颜色分布。颜色矩已被证明可有效地表示图像中的颜色分布，该方法的优点在于不需要颜色空间量化，特征向量维数低，但通过实验发现该方法的检索效率比较低，因而在实际应用中往往用来过滤图像以缩小检索范围。3个颜色矩的数学定义如下：

式中，pi,j表示彩色图像第j个像素的第i个颜色分量；N表示图像中的像素个数。

由图像的3 个分量Y、U、V图像的前三阶颜色矩组成一个多维直方图向量，即图像的颜色特征表示为

则颜色特征矩阵为

1.2 纹理矩阵构造

纹理是一种图像普遍存在的视觉现象，常见的纹理主要分为自然纹理、人工纹理和混合纹理等3类。描述纹理的参量有粗糙性、方向性、周期性、纹理强度和密度等，纹理描述是跟尺度相关的，纹理特征可以通过色调和结构来描述。本文采用灰度共生矩阵来构造纹理矩阵B。

定义1：从灰度为i的像素点出发，到该像素点的距离为(dx,dy)的另一个像素点的灰度为j的概率，记为P(i,j)。

数学表达式为

式中，d是用像素数量表示的相对距离；θ指像素点j与像素点i的相对位置方向；#表示集合；(x,y)为图像中的像素坐标。在构造纹理矩阵中用反差、能量、熵、相关性等特征量来表示纹理特征矩阵的元素。

其中，反差、能量、熵、相关性的定义分别如下：

由反差、能量、熵、相关性等4 个特征量构造的共生矩阵B为

1.3 形状矩阵

本文所采用的是形状不变矩法，利用目标图像所占区域的矩作为形状描述参数。将目标图像离散为M×N数字图像f(x,y)，其中心矩定义为

利用2 阶和3 阶中心矩可以导出n个具有平移和缩放的不变性的特征集合，将其构造为一个矩阵C。将目标图像依次缩小为80%、60%、50%、30%等，目标图像的左右上下平移操作分别用向量ci表示，得到如下的向量ci和矩阵C。

1.4 空间关系矩阵

图像对象空间关系描述在图像识别近似匹配的研究中是一个重要的因素。所谓空间关系是指图像中分割出来的多个目标之间的相互的空间位置或相对方向关系，这些关系也可分为连接和邻接关系，交叠和重叠关系以及包含和包容关系等。对于给定图像，首先通过图像分割算法得到n个对象oi(i=1,2,…,n)，计算其重心ci(i=1,2,…,n)作为对象的代表点，计算n个重心两两之间的距离dij=d(ci,cj)，组成距离矩阵D。将图像中的第一个对象o1与其余包含o1的oi(i=1,2,…,n)的重心距离作为矩阵的第一列，依次类推，可得

2 生成的方程

图像识别问题就是根据所选的区域图像，将其二值化为矩阵后，在App图库中找到与已知图像匹配的图像或最接近的图像与已知图像匹配。归结到数学问题中，即为矩阵方程求解问题。根据图像的颜色特征矩阵、纹理特征矩阵、形状特征矩阵和空间关系特征矩阵，构造一个含有4 个未知变量矩阵的线性矩阵方程，如式（13）。基于修正共轭梯度算法原理，建立求解这类方程的算法。

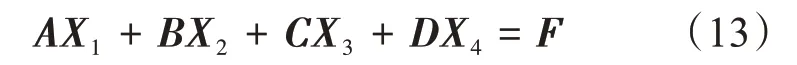
其 中，A、B、C、D、F∈Rn×n，用Rm×n表 示m×n实矩阵集合；定义同阶实矩阵A与B的内积为(A,B)=tr(ATB)，由此导出矩阵的Frobenius 范数

3 方程的求解

本文主要讨论方程式（13）的两个问题：

问题Ⅰ：若线性矩阵方程式（13）有解，求(X1,X2,X3,X4)∈Rn×n，使其满足方程式（13）。

问题Ⅱ：若线性矩阵方程式（13）无解，求(X1,X2,X3,X4)∈Rn×n，使‖AX1+BX2+CX3+DX4-F‖=min。

3.1 求解问题Ⅰ的修正共轭梯度算法

借鉴共轭梯度算法原理，建立求解问题Ⅰ的修正共轭梯度算法，引入记号：

算法1（问题Ⅰ的修正共轭梯度算法）：

Step1：给定初始矩阵X(1)1、X(1)2、X(1)3、X(1)4∈Rn×n，置k：=1，计算

Step2：如果Rk=O，或者Rk≠O而Qk=O，停止计算；否则，计算

Step4：置k：=k+1，转step2。

下面直接给出算法1 的性质和定理，可以证明算法1在有限步计算之后停止。

当res.data.resultCode返回的为-9999的时候，代表请求资源失败，res.data.object.resultCode返回的为-9999的时候，代表业务处理失败，即‘用户名或密码错误’，否则代表业务处理成功。

性质1对于算法1中的矩阵Ri、Q i和，有

性质2设k≥2，对算法1中的矩阵Ri和Q j，有

性质3设是问题Ⅰ的任意一组解，那么对任意初始矩阵由算法1得到的矩阵和Qk满足

定理1设问题Ⅰ有解，则对任意的初始矩阵算法1可在有限步计算后求得问题Ⅰ的一组解。问题Ⅰ无解的充要条件是存在正整数k，使得由算法1得到的Rk≠O而Qk=O。

3.2 求解问题Ⅱ的MCG算法

在算法1中，当Rk≠O而Qk=O时算法1中断，表明方程式（13）无解。因此，求解问题Ⅱ，即求方程式（13）的最小二乘解。通过构造等价线性矩阵方程，将求矩阵方程式（13）最小二乘解问题转化为求等价正规方程的解问题，建立求矩阵方程式（13）的最小二乘解的迭代算法。

引入记号：

求解方程式（13）的最小二乘解等价于求矩阵方程式（13）的正规方程组的解，将方程式（13）按行拉直，则得到方程组Mx=v，其正规方程组为MTMx=MTv，因为正规方程组一定有解，所以方程式（13）的最小二乘解一定存在，即问题Ⅱ的解存在。

参照算法1 以及共轭梯度算法原理，建立求矩阵方程u(X)=G的解的算法，即求解问题Ⅱ的MCG算法如下。

算法2（问题Ⅱ的修正共轭梯度算法）：

Step1：给定初始矩阵置k：=1，计算

Step2：如果Rk=O，停止计算；否则，计算

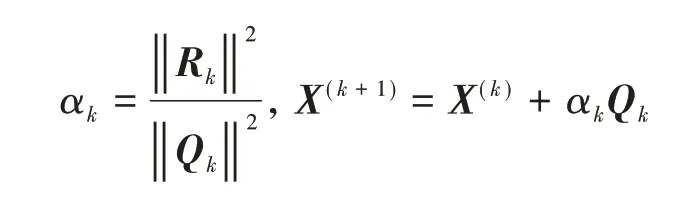
Step3：计算

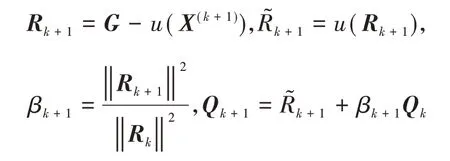
Step4：置k：=k+1，转step2。

对于算法2有类似于算法1的收敛定理。

定理3对任意的初始矩阵，忽略舍入误差，则算法2 可在有限步计算后求得问题Ⅱ的一组解，即矩阵方程式（13）的最小二乘解。

4 数值算例

用文中建立的算法1 求解矩阵方程式（13）的一组解，其中系数矩阵A、B、C、D、E均为元素为1的4n阶方阵，终止准则为ε=10-12。

选取初始矩阵X1=X2=X3=X4=O4n×4n，按照算法1 可求得矩阵方程式（13）的一组解，计算时间（s）、迭代次数、实际误差及解矩阵的范数如表1（Matlab软件2014版）所示。

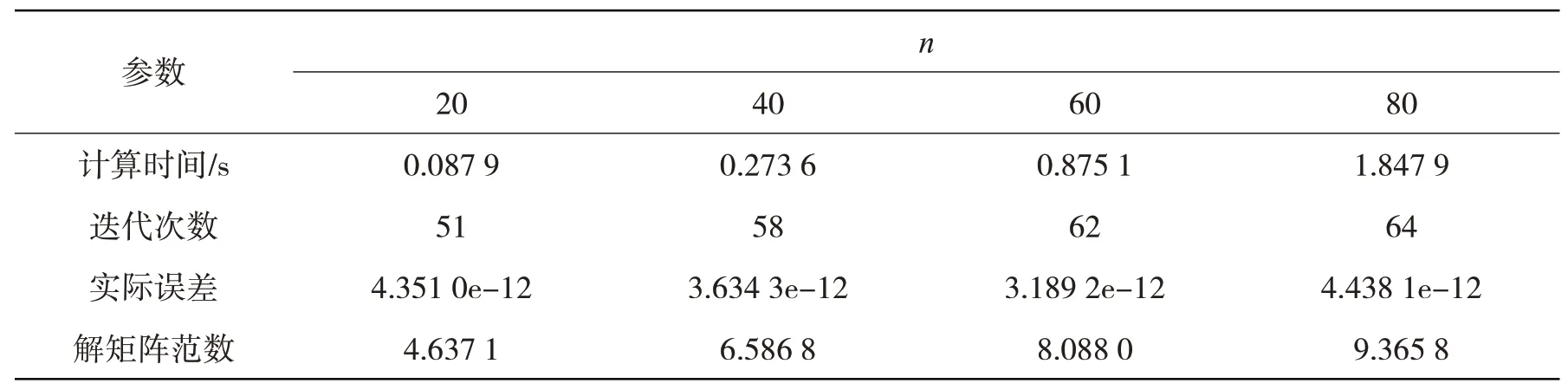
表1 计算结果

当n=1 时，计算得

从表1 可以看出，该算法具有较高的计算效率，当方程有解时，可以得到方程式（13）的一组解，即能在已有的图库中找到匹配图像；当n=1 时，给定一个已知图像信息矩阵，可以找到颜色特征矩阵、纹理特征矩阵、形状特征矩阵和空间关系特征矩阵的组合系数解X1、X2、X3、X4。

5 结论

本文建立的MCG 算法具有较高的精准度和较快的识别速度，当方程有解时，则该App 算法可在图库中找到精准匹配图像；当方程无解时，可以找到最小二乘解，即算法可找到最接近匹配图像。该算法在计算机仿真中还需验证其有效性，在实际应用中，若图库中有大量的设计类相似图像时，如何能更精准找到目标图像，还需要进一步研究。