共轭线性对称性及其对PT-对称量子理论的应用*

黄永峰 曹怀信 王文华

1) (陕西师范大学数学与信息科学学院, 西安 710119)

2) (昌吉学院数学系, 昌吉 831100)

3) (陕西师范大学民族教育学院, 西安 710119)

传统量子系统的哈密顿是自伴算子, 哈密顿的自伴性不仅保证系统遵循酉演化和保持概率守恒, 而且也保证了它自身具有实的能量本征值, 这类系统称为自伴量子系统.然而, 确实存在一些物理系统(如 PT −对称量子系统), 其哈密顿不是自伴的, 这类系统称为非自伴量子系统.为了深入研究 PT −对称量子系统, 并考虑到算子 PT 的共轭线性性, 首先讨论了共轭线性算子的一些性质, 包括它们的矩阵表示和谱结构等; 其次,分别研究了具有共轭线性对称性和完整共轭线性对称性的线性算子, 通过它们的矩阵表示, 给出了共轭线性对称性和完整共轭线性对称性的等价刻画; 作为应用, 得到了关于 PT −对称及完整 PT −对称算子的一些有趣性质, 并通过一些具体例子, 说明了完整 PT −对称性对张量积运算不具有封闭性, 同时说明了完整 PT −对称性既不是哈密顿算子在某个正定内积下自伴的充分条件, 也不是必要条件.

1 引 言

传统的量子力学中, 量子系统的状态随时间的演化由一个自伴哈密顿量 H 决定的薛定谔方程来描述.哈密顿量的自伴性保证了系统遵守酉演化,同时也保证了其特征值为实数.但是, 确实存在一些物理系统, 其哈密顿不是自伴的, 但也具有实的能量本征值.Bender等[1−3]讨论了哈密顿量H=p2+x2(ixˆ)ϵ谱的性质, 其中 ϵ 为实数, 说明了当ϵ≥0时其特征值都是实数, 当 ϵ ＜0 时会出现复特征值, 从而提出了一类非自伴哈密顿, 称为 PT −对称哈密顿.其中 P 是一个线性算子, 表示宇称变换,T 是共轭线性算子, 表示时间反演变换.由于 PT −对称哈密顿的特征值为实数或者共轭成对出现的复数, 为了保证其特征值为实数, 又引入了完整PT −对称的概念.在此基础上, 通过引入一个 C 算子, 构造了一个新的正定 C PT −内积, 使得哈密顿H在该内积下是自伴的, 从而也遵守酉演化, 同时还说明了 C 算子是不唯一的[4−7].后来, Mostafa−zadeh[8−12]提出了伪自伴算子的概念, 研究了伪自伴哈密顿的相关性质, 指出 PT −对称哈密顿可以看成一类特殊的伪自伴哈密顿, 同时给出了针对Freedman−Robertson−Walker模型中哈密顿是伪自伴的例子.Bender等[13]发现在 PT −对称量子理论下, 量子系统的最优演化时间能够迅速减小甚至达到零.Zheng等[14]通过设计核磁共振量子系统中具有 PT −对称哈密顿量的时间演化实验, 证实了相应的结果.目前, 关于 PT −对称量子理论的研究已经涉及到了物理学及信息学的各个方面, 包括PT −对称性在光学领域的应用[15], PT −对称量子场论的相关问题[16,17], PT −对称量子系统中的纠缠问题[18], PT −对称量子系统中无信号原理及其实验观测[19,20], PT −对称性与图论及量子随机游走的关系[21−23]等.此外, 还有一些其他的相关研究[24−37].最近, Huang等[38]通过弱测量模拟了缺破(broken) PT −对称哈密顿系统.

本文首先讨论共轭线性算子的一些性质, 包括其矩阵表示和谱结构; 其次, 给出线性算子的共轭线性对称性和完整共轭线性对称性的定义, 讨论共轭线性对称算子和完整共轭线性对称算子所具有的相似Jordan标准型, 同时给出共轭线性对称算子和完整共轭线性对称算子的等价刻画; 作为应用, 得到非自伴哈密顿算子 PT −对称性及完整 PT −对称性的一些性质, 通过完整 PT −对称哈密顿的一些具体例子, 说明完整 PT −对称性对张量积不具有封闭性, 同时说明完整 PT −对称性既不是哈密顿算子在某个正定内积下自伴的充分条件, 也不是必要条件.

2 共轭线性算子的性质

本文用 K 表示 n 维复 Hilbert空间, 用 ∥ x∥ 表示向量 x ∈K 的范数, 即用 I 表示K 上的恒等算子.对于 K 上的线性算子 A , 用 A†表示线性算子 A 的Hermitian伴随算子.若 A =A†,则称 A 是自伴的; 否则, 称 A 是非自伴的.若存在可逆线性算子 B 使得 A =B†B , 则称 A 为正定算子;若 [ A ,B]:=AB-BA=0 , 则称算子 A 与 B 可交换.

用 Mn(C) 表示全体n阶复矩阵构成的 C∗−代数, In表示 n 阶单位矩阵.用表示 a ∈C 的复共轭, 对对 A ,B∈Mn(C) , 若存在可逆矩阵 S ∈Mn(C) 使得 S-1AS=B , 则称A相似于B, 记为 A ～B .如果矩阵A 相似于某个对角矩阵, 那么称A可相似对角化.

定义1对于算子 A :K→K , 若

则称 A 为共轭线性算子.

对于空间 K 上的任一共轭线性算子 A , 任取K的一个正规正交基令则

进而可知, 空间 K 上的任一共轭线性算子 A 都是一致连续的.

通常, 任一 n ×n 阶矩阵 A =[aij]n×n 都对应空间 K 上的一个线性算子：

如果定义

那么得到 K 上的共轭线性算子 A , 且满足Aej=将此关系记为

反之, 对 K 上任一共轭线性算子 A , 记

则得到一个 n ×n 矩阵 A =[aij] , 称其为共轭线性算子 A 在基 E 下的表示矩阵.显然, 算子 A 与其表示矩阵A满足(3)式的关系, 从而表示矩阵A按照(2)式定义的算子正好为 A .

这说明, 共轭线性算子 A 与矩阵A在关系式(3)下是一一对应的, 且 对任意有

易见, 矩阵A为共轭线性算子 A 在基 E 下的表示矩阵当且仅当它们满足关系式 (4).

定义 K 上的算子 T0为

简记为 T0x=.易见, T0是共轭线性算子, 且它在基 E 下的表示矩阵为n阶单位阵 In.于是, 对任意有

容易看出, 任何两个共轭线性算子 A 与 T0的复合算子 T0A 或 A T0都为线性算子, 且满足关系A=(AT0)T0=T0(T0A).由此可见, 任意一个共轭线性算子都可以看成是一个线性算子与 T0的复合,也可以表示为 T0与一个线性算子的复合.参见图1.

图1 共轭线性算子 A 与 T0 的复合算子 A T0 (左)与T0A(右)都是线性算子, 且满足关系A=(AT0)T0=T0(T0A)Fig.1.Composition operators A T0 (left) and T0A (right),composed of conjugate linear operators A and T0 , which are linear operators and satisfy A =(AT0)T0=T0(T0A) .

设 A ,B 均为共轭线性算子, A ,B 为它们的表示矩阵, 则由 (4) 式知：对任意有

进一步, 可以讨论更一般的情形.设Ai(i=1,2,···,m)均为共轭线性算子,Ai(i=1,2,···,m)为对应的矩阵表示, 则当 m =2k 为偶数时,A1A2···Am为 线 性 算 子, 其 矩 阵 表 示 为当 m =2k+1 为 奇 数 时 ,A1A2···Am为共轭线性算子, 其矩阵表示为

用 σ (A) 表示算子 A 的所有 特 征 值之集, 称为A的谱, 即

其中, Nλ(A)=ker(λI-A) , 称为算子 A 对应特征值 λ 的特征子空间.

例如, σ (I)={1} .由于

所以, σ (T0)⊃ {-1,1,-i,i} .

下面讨 论 一 般 共 轭线性算子 A 的谱 σ (A) 的一些性质.

首先, 由定义式(6)知, λ ∈ σ(A) 当且仅当算子方程 A x=λx 有非零解当且仅当矩阵 方 程 λ c=Ac¯ 有 非 零 解 c =(c1,c2,···,cn)T; 此时, λ 称为算子 A 的特征值, 相应的非零解x称为对应于特征值 λ 的特征向量.

因此, 共轭线性算子 A 的谱 σ (A) 为复平 面上的一个有界集, 但可能为无限集(见定理1), 也可能为空集(见例1).

通过上面的讨论, 可以得到下面的定理.

定理1设 A 为 K 上的共轭线性算子, 其表示矩阵为A, 则

(a) λ 为 A 的特征值且有实的特征向量x当且仅当 λ 为A的特征值且有实的特征向量c;

(b) 当 λ ∈ σ(A) 时, 有 | λ |2∈ σ(A2) ;

(c) A 的谱半径满足

(e) σ (A) 为复平面上的有界闭集.

定理1说明了与线性算子的谱结构不同：线性算子的谱为复平面上的有限集, 但共轭线性算子可能包含一系列以原点为公共圆心的圆周.其次, 由定理1中的结论 (b)知：当 σ (A2)∩(0,+∞)=∅ 时,必有 σ (A)=∅ (例1).于是, 如果线性算子 A2没有正的特征值, 那么共轭线性算子 A 就没有特征值.进一步, 由于 σ (T0)⊃ {-1,1,-i,i} 且所以由定理1(c)与定理1(d)知

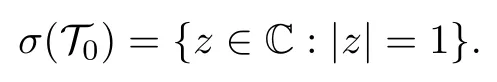
例 1设 K 为 2 维复线性空间, { e1,e2} 为 K 的一组线性无关基, ∀ z∈ C , 定义算子 Az为

显然, Az为 K 上的共轭线性算子, 且其表示矩阵为

这里的算子 Ai正好为物理上的自旋 1 /2 −粒子的翻转算子, 它没有特征值.

3 线性算子的共轭线性对称性

下面讨论共轭线性对称算子的性质, 给出其表示矩阵具有的相似Jordan标准型.在此基础上,讨论完整共轭线性对称哈密顿的性质, 给出完整共轭线性对称性的等价刻画.

定义2设 H 为 K 上的线性算子, 若存在可逆的共轭线性算子 A , 使得 [ A ,H]=0 , 则称 H 为共轭线性对称的; 此时, 也称 H 为 A −对称的.

为了讨论共轭线性对称算子的性质, 先给出以下引理.

引理1[39]设 H ∈Mn(C) , 则H相似于 H 当且仅当H相似于某个实矩阵.

引理2[39]设 H ∈Mn(C) , 则H相似于某个实矩阵当且仅当H相似于如下的标准型矩阵

其中

k=1,2,···,p;Jnk(λk)为标准Jordan块,λ1,···,λp为非实数的复数, λnp+1,···,λnr是实数.

引理3[39]设 A ∈Mn(C) , 则A满足A=I当且仅当存在可逆矩阵 S ∈Mn(C) , 使得A=S-1.

下面的定理给出了共轭线性对称算子的一些等价刻画.

定理2设 H 为 K 上的线性算子, 则以下叙述等价：

(i) H 是共轭线性对称的;

(iii) H 的表示矩阵H相似于某个实矩阵;

(iv) H 的表示矩阵H具有相似Jordan标准型(7)式;

(v) 存在共轭线性算子A 满足 A2=I , [ A ,H]=0 ;

(vi) 存 在 K 上 的 可 逆 线 性 算 子 η , 使 得H†= ηHη-1;

(vii) 存在 K 上的可逆自伴线性算子 η1, 使得(即 H 为 η1−伪自伴[37]).

证明(i) ⇒ (ii).设 H 是共轭线性对称的, 则由定义 2 知, 存在共轭线性算子 A 使得 H 为 A −对称.记H和A分别为 H 和 A 的矩阵表示, 则有A=HA, 即=A-1HA .由 A 可逆知 A 可逆, 从而知H相似于.

由引理1可知 (ii)和(iii)等价, 由引理2可知(iii)和(iv)等价.

由定义2, 显然(v) ⇒ (i)成立.下面证明(i)⇒(v).

(i) ⇒ (v).设 H 为共轭线性对称的, 则由引理1知, H 的表示矩阵H相似于某个实矩阵, 即存在可逆矩阵S使得从而令则同时由引理3知 A A=I .设 A 为A所对应的共轭线性算子, 则有 A2=I , 且 [ A ,H]=0 .

(ii) ⇒ (vi).设 H 为 H 的表示矩阵, 且相似于H.从而存在可逆矩阵A, 使得=AHA-1.又因为任意复矩阵的转置矩阵与其本身相似, 从而存在可逆矩阵S使得即H†=设H,η为分别对应 H ,SA 的线性算子, 则有 H†= ηHη-1.

(vi) ⇒ (ii).设存在 K 上的可逆线性算子 η , 使得 H†= ηHη-1.记 H ,A 为分别对应 H ,η 的表示矩阵, 则A为可逆矩阵, 且 H†=AHA-1.又因为H†和相似, 从而存在可逆矩阵S, 使得H†=因此从而=SA×H(SA)-1, 即H相似于.

显然(vii) ⇒ (vi)成立.下面证明(vi) ⇒ (vii).

(vi) ⇒ (vii).设 H†= ηHη-1, η 为可逆线性算子.对非零的 a =reiθ∈ C , - e2iθ∈/σ(η-1η†) ,η0=aη仍为可逆线性的, 且有从而令 η1= η0+, 则 η1为自伴的 且因为所以从而可逆.又因为所以 η1可逆.由此, 证明了 η1为可逆自伴线性算子, 且证毕.

由定理2及引理2知, 共轭线性对称算子的特征值都是实的, 或共轭成对出现的, 且共轭成对的特征值具有相同的代数重数和几何重数.在物理上, 一般希望可观测量对应的测量结果是实数, 这就要求量子系统的哈密顿 H 的特征值均为实的.于是, 我们引入下面的完整共轭线性对称的概念.

定义 3若 H 为空间 K 上的 A −对称线性算子,并且 H 的特征态均为 A 的特征态, 则称 H 为完整 A −对称的; 若存在可逆共轭线性算子 A 使得 H 为完整A −对称的, 则称 H 为完整共轭线性对称的.

下面说明具有完整共轭线性对称的算子, 其特征值均为实数.

命题 1设 H 为 K 上的线性算子, 若 H 为完整共轭线性对称, 则 H 的特征值都是实的.

证明设存在可逆的共轭线性算子 A , 使得AH=HA , 且 H 的 特 征 态 均 为 A 的 特 征 态 .设a是 H 的一个特征值, 对应的特征态 f0 , 满足Hf=af .因此, H Af=AHf=Af .由于 f也是A 的一个特征态, 所以存在b使得 A f=bf .从而有 a bf=bf .因为 A 可逆, 故 b0 .又 f0 , 所以 a =证毕.

上述定理说明, 算子的完整共轭线性对称性是其特征值为实数的充分条件, 但这并不是必要条件(见定理3).下面给出完整共轭线性对称的一个等价刻画.

定理3设 H 是 K 上的线性算子且为共轭线性对称的, 则 H 为完整共轭线性对称的当且仅当H的特征值均为实的且 H 为非简并的(即 H 的每个特征值的几何重数为1).

证明必要性.设 H 为完整共轭线性对称, 由命题1知 H 的特征值都是实的.下面只需证明∀a∈ σ(H), 有 d imNa(H)=1 .假设 d imNa(H)＞1 ,则存在 K 中的两个非零向量 x ,y 使得Hx=ax,Hy=ay 且 { x,y} 是线性无关集.由于 H 为完整共轭线性对称, 所以存在可逆的共轭线性算子 A 以及c,d0使得 A x=cx,Ay=dy .当 cd 时, 取 z =x+y , 显然它是 H 关于a的一个特征态, 但是对于所有的复数 λ , 都有 A z=Ax+Ay=cx+ d yλz .当 c =d 时, 取 z =x+iy , 显然它是 H 关于 a 的一个特征态, 但对于所有的复数 λ , 都有Az=AxiAy=cx-icyλz .以上两种情况下, 结果都与H具有完整共轭线性对称性矛盾.由此可知 H 的每个特征值几何重数均为1.

充分性.设 H 的特征值均为实的且 H 非简并.由于 H 为共轭线性对称, 因此存在可逆的共轭线性算子 A 使得 H 为 A −对称, 只需证 H 的特征向量均为 A 的特征向量.设 x =0 为 H 的对应于 λ 某个特征向量, 则 λ 为实数, 且使得 H x=λx .因为HAx=AHx=A(λx)=Ax= λAx , 即 A x 也为 H 对应于特征值 λ 的特征向量.又因为 d imNλ(H)= 1, 从而存在 k0 使得 A x=kx , 即 x 为 A 的特征向量, 从而 H 为完整 A −对称的.证毕.

通过定理3可以得到下面的推论.

推论1K 上的线性算子 H 为完整共轭线性对称当且仅当其表示矩阵H相似于如下的Jordan标准型

其中 λ1,···,λk为H的全部k个互不相同的实特征根, Jni(λi)(i=1,2,···,k) 为标准Jordan块.

推论2设 H 是 K 上的线性算子且为共轭线性对称的, 若 H 有n个互不相同的实特征值, 则H为完整共轭线性对称.

4 线性算子的PT−对称性以及完整PT−对称性

本节讨论 PT −对称线性算子的一般性质.为此, 我们回顾文献[27]中关于 PT −框架的概念.

定义 4[27]设 H 是 K 上的线性算子, P ,T 是K上的算子, 且满足以下条件：

(2) P2=T2=I , PT=TP , 则称 { P,T} 是K上的 PT −框架.

若 { P,T} 是 K 上的 PT −框架, 且 [ H ,PT]=0 ,则称算子 H 为 PT −对称.

由定义 4 可知, 当 { P,T} 为空间 K 上的 PT −框架时, 算子 PT 为 K 上的可逆共轭线性算子.于是, 当 H 为 PT −对称算子时, 它必然是 PT −对称的(定义2), 从而是共轭线性对称的算子.

反之, 若 H 为共轭线性对称的, 所以定理2 (v)成立, 即存在共轭线性算子 T 满足 T2=I ( K 上的恒等算子), 且 [ T ,H]=0 .记 P =I , 则 { P,T} 为是K 上的 PT −框架且 H 为 PT −对称.

以上讨论说明了共轭线性对称性和 PT −对称性的有以下关系.

命题2空间 K 上的线性算子 H 为共轭线性对称算子当且仅当存在 K 上的某个 PT −框架{P,T}使得 H 为 PT −对称.

设 P ,T 和 H 分别是 P ,T 和 H 的表示矩阵, 则{P,T}构成 PT −框架等价于以下矩阵等式成立：

H 为 PT −对称等价于以下矩阵等式成立：

由定理1, 易得到下面的命题.

命题 3设 { P,T} 是 K 上的 PT −框架, 则σ(PT)要么为空集, 要么为复平面上的单位圆周.

命题 4设 { P,T} 是 K 上的 PT −框架, 其中T定义为

且 H 是 K 上的线性算子, 则

(i) { P†,T} 为 K 上的 P†T −框架;

(ii) H 为 PT −对 称 的 当 且 仅 当 H†为 P†T −对称的.

证明(i) 由(11)式知, T 的矩阵表示为单位阵 In, 且 T=In.由于 { P,T} 构成 K 上的 PT −框架, 所以(9) 式成立.从而,

因此, { P†,T} 也构成 K 上的 P†T 框架.

(ii) 因为

类似于完整共轭线性对称, 可以给出完整 PT −对称定义.

定义 5[27]设 H 是 K 上的线性算子, { P,T} 是K 上的 PT −框架, 若 H 是 PT −对称的且它的特征态都是 PT 的特征态, 则称 H 是完整 PT −对称.

由定理3及推论2容易得到下面的定理.

定理 4设 { P,T} 是 K 上的 PT −框架, H 是K上的线性算子且为 PT −对称的, 则

(a) H 为完整 PT −对称的当且仅当 H 的谱为实的, 且 H 为非简并的;

(b) H 为完整 PT −对称的且可相似对角化当且仅当 H 有n个互不相同的实特征值.

例 2设 { P,T} 是 2 维复空间 K 上的 PT −框架 , H1为 K 上 的 线 性 算 子, P ,T,H1的 表 示 矩 阵P,T,H1为

则 H1为 完 整 PT −对 称 的 当 且 仅 当|b|2≥(Ima)2且 b0 .

证明充分性.设|b|2≥(Ima)2且 b0 .

计 算 可 知 ：H1的 两 个 特 征 值 λ=Rea±当 | b |2-(Ima)2≥0 , H1特征值均为实数.下面分两种情况进行讨论.

(1) 当 | b |2-(Ima)2＞0 时, H1有 两 个 不 相 同的实特征值.进而, 由定理4(b)知 H1为完整 PT −对称的.

(2) 当 | b |2=(Ima)2时, σ (H1)={λ} , 且实特征值 λ =Rea 的代数重数为2.由于

必要性.设 H 为完整 PT −对称的, 则 H 为 PT −对称, 且由定理4(a) 知：H的特征值均为实的且 几 何 重 数 为 1.因 为 H1为 PT −对 称 的 , 所 以于是, 由充分性的证明可知：H1的两个特征值为由于H的特征值均为实的, 所以 | b |2-(Ima)2≥0 .假若b=0, 则 I ma=0 , 从 而 λ I-H1为 零 矩 阵 , 即H1=λI .这与 H1的特征值 λ =Rea 几何重数为1矛盾.故 b0 .证毕.

例 3设 { P,T} 是 2 维 复 空 间 K 上 的 PT 框架 , H2为 K 上 的 线 性 算 子 , P ,T,H2的 表 示 矩 阵P,T,H2为

其中 r ,s,θ 是非零实数, 则由例2知, H2为完整PT −对称的当且仅当 | s |≥ |r·sinθ| .

例 4设 { P,T} 是 3 维复空间 K 上的 PT 框架,H3为 K 上的线性算子, P ,T,H3的表示矩阵P T,H3为

设 { Pk,Tk} 是 复 空 间 Kk上 的 PkTk−框 架 (k =1, 2) , 定义张量积空间 K1⊗K2上的算子如下：

其中, 线性算子 A1与 A2的张量积 A1⊗A2的定义与通常相同, 即

易知, { P,T} 是空间 K1⊗K2上的 PT −框架且 H 是PT −对称的 (参见例 5).这就说明：PT −框架及PT−对称性对张量积运算“具有封闭性”.

例 5设 { Pk,Tk} 是 2 维复空间 K 上的 PkTk−框架 ( k=1,2) , Hk为 K 上的线性算子(k=1,2),Pk,Tk,Hk的表示矩阵 Pk,Tk,Hk为

显然, Hk为 PkTk−对称的 ( k=1,2) , 从而,H1⊗H2为 PT −对称的, 其中P=P1⊗P2,T=T1⊗T2.

但是, 完整 PT −对称性对于张量积运算“不具有封闭性”, 即 Hk是完整 PkTk−对称的 ( k=1,2) 不能保证张量积 H1⊗H2一定是完整 PT −对称的, 其中 P =P1⊗P2,T=T1⊗T2(例6).

例 6设 { Pk,Tk}(k=1,2) 是 2 维复空间 K 上的 PkTk框 架 , Hi为 K 上 的 线 性 算 子 ,Pk,Tk,Hk的表示矩阵 Pk,Tk,Hk分别为

容易看出, H1的特征值为1, 代数重数为2, 几何重数为1, H2的特征值为2, 代数重数为2, 几何重数为1.由定理4知, Hk(k=1,2) 都是完整PkTk(k=1,2)−对 称 的 .因 此 , H =H1⊗H2为 PT −对称的, 其中 P =P1⊗P2,T=T1⊗T2.下面说明H不是完整 PT −对称的.

计算可知

它只有一个特征值2, 其代数重数为4、几何重数为 2.从而由定理 4(a) 知：H 不是完整 PT −对称的.

下面从矩阵分析的角度来考查例6的更一般的情形.

设 Hk(k=1,2) 为2维空间 K 上线性算子且是完整 PkTk−对称的 ( k=1,2) , Pk,Hk分别为Pk,Hk的表示矩阵, 且

即存在可逆矩阵 Qk(k=1,2) 使得Hk=QkJk×(k=1,2), 从而H1⊗H2=(Q1⊗Q2)(J1⊗J2)(Q1⊗Q2)-1.

设 H ,P,T 按照 (13)式定义, H ,P,T 为对应的表示矩阵.下面说明 H 不是完整 PT −对称的.

又因为H=H1⊗H2～J1⊗J2, 所以

其中 g (λ1λ2) 为 λ1λ2的几何重数.由定理4(a)可知：H 不是完整 PT −对称.

下面简单说明 PT −对称量子系统与经典量子系统之间的转化关系.设 { P,T} 是 K 上的 PT −框架, H 为哈密顿且为 PT −对称的.PT −对称量子理论的关键在于构造一个线性算子 C , 建立一个新的正定内积, 称之为 C PT −内积, 使得 H 关于 C PT −内积为自伴的, 从而保证系统的演化关于新内积为酉演化且概率守恒.因此, 问题的本质在于寻找一个新的正定内积, 使得系统哈密顿 H 在这个内积下是自伴的.

给定空间 K 上的正定算子 η , 可以定义 K 上的新内积称之为 K 上的 η −内积.我们在文献[37]中给出了线性算子关于某个正定内积是自伴的一些等价条件, 证明了存在正定算子η使得 H 关于 η −内积是 K 上的自伴线性算子当且仅当 H 的表示矩阵H相似于一个实对角阵.哈密顿H 的完整 PT −对称性保证了 H 的特征值是实数, 但并不能保证其表示矩阵H可相似对角化.由命题5知：H 为完整 PT −对称的且可相似对角化当且仅当 H 有n个互不相同的实特征值.因此, H 的完整PT −对称性不是 H 关于某个新的正定内积下自伴的充分条件, 同时也不是必要条件.

5 结 论

本文讨论了共轭线性算子的一些性质, 给出了共轭线性对称和完整共轭线性对称的定义, 给出了共轭线性对称性和完整共轭线性对称性的等价刻画; 在此基础上, 进一步讨论了 PT −对称及完整PT −对称的性质, 给出了完整 PT −对称哈密顿的一些具体例子, 说明了完整 PT −对称性对张量积运算不具有封闭性, 同时还说明了完整 PT −对称性既不是哈密顿 H 在某个正定内积下自伴的充分条件, 也不是必要条件.通过本文的讨论, 可以帮助我们更好地理解共轭线性对称性的本质, 使我们对 PT −对称量子系统相应的数学结构有更清楚的认识, 对将来的进一步研究具有一定的理论意义.