关于对合BCK代数
凌雪岷
(安徽新华学院 通识教育部,安徽 合肥230088)
为给逻辑推理提供各种可能的逻辑体系,许多学者陆续提出了各种型和形不同的代数系统,每一种代数系统对应着不同的公理组。王国俊[1-2]提出的与形式逻辑系统L*相匹配的R0-代数就是这类重要的逻辑系统。吴望名[3]提出了比较一般化的FI-代数与正则FI-代数,后来人们发现FI-代数与日本数学家Imai Y和Iseki K在1966年提出的BCK代数有着紧密的关系。关于上述逻辑代数,我国学者做了深入研究,给出了它们的多种刻画和相互关系,取得了许多可喜的成果[4-9]。在这些研究的基础上,本文将证明正则FI-代数与对合BCK代数等价,然后在对合BCK代数中引入分配性条件,讨论了分配对合BCK代数具有的若干性质,利用这些性质证明了分配对合BCK代数与Boole代数等价。
1 预备知识
下面给出BCK代数和FI-代数的基本概念和相关结果。
定义1[5]一个(2,0)型代数(X,*,0)称为BCK代数,若∀x,y,z∈X,有:

命题1[7]在BCK代数(X,*,0)中,下列各式成立,∀x,y,z∈X,有:
(P1)(x*y)*z=(x*z)*y;
(P2)x*0=x;
(P3)x*(x*(x*y))=x*y。
若存在常元1使得任意x∈X,x*1=0,则称BCK代数(X,*,0)是有界的。在有界BCK代数X中,令N(x)=1*x。若∀x∈X,N(Nx)=x,则称X为对合BCK代数[5]。定义二元关系“≤”使对任意x,y∈X,x≤y⇔x*y=0。易验证在对合BCK代数中“≤”是偏序,0和1分别是最小元和最大元。
命题2若X为对合BCK代数,则∀x,y∈X,有:
(P4)Nx*Ny=y*x,x*Ny=y*Nx,Nx*y=Ny*x;
(P5)若x≤y,则z*y≤z*x。
证明(P4)由(P1)和对合性知Nx*Ny=(1*x)(1*y)=(1*(1*y))*x=y*x。(P4)后两式可由第1式,分别用Nx替换x和Ny替换y得到。
(P5)设x≤y,则x*y=0,从而有

由“≤”的定义知z*y≤z*x。
定义2[3]一个(2,0)型代数(X,→,0)称为Fuzzy蕴涵代数,简称FI-代数。如果∀x,y,z∈X,满足:
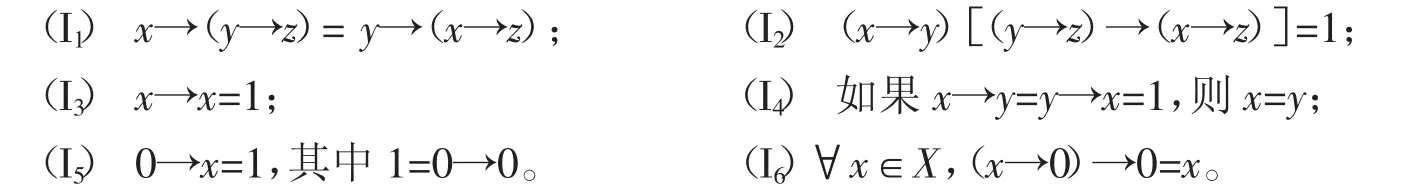
称满足(I6)的FI-代数为正则FI-代数。
引理1[3,6]在正则FI-代数(X,→,0)中,∀x,y,z∈X,有:
(1)1→x=x,特别地,1→0=0;
(2)x→y=(y→0)→(x→0);
(3)(y→z)→((x→y)→(x→z))=1;
(4)若x→0=0,则x=1。
2 对合BCK代数与正则FI-代数
本节证明对合BCK代数与正则FI-代数等价。
命题3在对合BCK代数(X,*,0)中,∀x,y,z∈X,有:
(1)N(0)=1,N(1)=0; (2)((x*z)*(y*z))*(x*y)=0。
证明(1)由(P2)知N(0)=1*0=1,由(K3)知N(1)=1*1=0。
(2)由(K2)和(P1)知((x*z)*(y*z))*(x*y)=((x*z)*(x*y))(y*z)=0。
命题4设X是正则FI-代数。对任意∀x,y∈X,定义x*y=(x→y)→0。则X是对合BCK代数。
证明由定义2,先证明(K1)~(K5)成立。
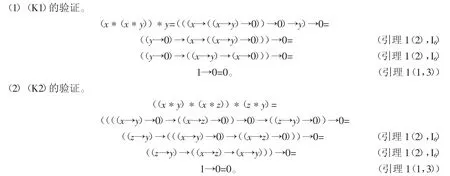
(3)(K3)的验证。由(I3)和引理1(1)知x*x=(x→x)→0=1→0=0。
(4)(K4)的验证。由(I5)和引理1(1)知0*x=(0→x)→0=1→0=0。
(5)(K5)的验证。若x*y=y*x=0,则由引理1(4)知x→y=y→x=1,再由(I4)知x=y。
再证有界性和对合性:x*1=(x→1)→0=1→0=0,又

综上,我们知正则FI-代数是对合BCK代数。
命题5设(X,*,0)是对合BCK代数。对任意x,y∈X,定义x→y=N(x*y)。则(X,→,0)是正则FI-代数。
证明由定义2知,需验证(I1)~(I6)成立。

(3)(I3)的验证。由(K3)和命题3(1)知x→x=N(x*x)=N(0)=1。
(4)(I4)的验证。若x→y=y→x=1,则x*y=y*x=0,由(K5)知x=y。
(5)(I5)的验证。由(K4)和命题3(1)知0→x=N(0*x)=N(0)=1。
(6)(I6)的验证。由(P2)和对合性知(x→0)→0=N(x*0)→0=N(N(x))=x。
综上,我们知对合BCK代数是正则FI-代数。
由命题4和命题5立得:
定理1正则FI-代数和对合BCK代数是相互等价的代数系统。
3 分配对合BCK代数与Boole代数
本节在对合BCK代数中引入分配性,证明分配对合BCK代数与Boole代数等价。
定义3设(X,*,0)是对合BCK代数。称X是分配的,如果X满足条件:
(Dis)∀x,y,z∈X,N(N(z)*(N(x)*y))=N(x*z)*(y*z)。
命题6在分配对合BCK代数(X,*,0)中,∀x,y,z∈X,有:
(1)N(z)*(N(x)*y)=N(N(x*z)*(y*z));
(2)x*(y*x)=x;
(3)x=x*N(x);
(4)N(x)=N(x)*x;
(5)x*(x*y)=y*(y*x)。
证明(1)由对合性和(Dis)条件知
N(z)*(N(x)*y)=N(N(N(z)*(N(x)*y)))=N(N(x*z)*(y*z))。
(2)在结论(1)中令x=z并用N(x)替换,y用y*x代,则得

综上,由(K5)知x*(y*x)=x。
(3)一方面,由(P1),(K3)和(K4)知(x*N(x))*x=(x*x)*N(x)=0*N(x)=0。另一方面,在结论(1)中令x=y=z并用N(x)替换,则得

综上,由(K5)知x*N(x)=x。
(4)在结论(3)中用N(x)代替x,由对合性知N(x)=N(x)*N(N(x))=N(x)*x。
(5)由(P1),命题3(1)和结论(2)知

同理得(y*(y*x))*(x*(x*y))=0,由(K5)知y*(y*x)=x*(x*y)。
命题7设(X,≤,')是Boole代数,则X是分配对合BCK代数。
证明在Boole代数X中定义x*y=x∧y',则N(x)=1*x=1∧x'=x',故有界性,(K1)~(K5)及对合性容易验证(或见文献[8]中定理2)。下证分配性(Dis)。
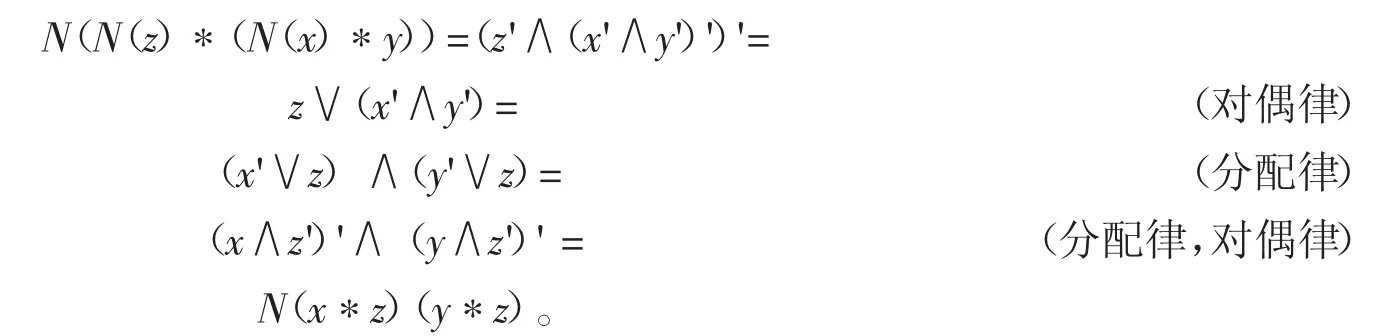
从而(Dis)条件成立,于是Boole代数是分配对合强BCK代数。
命题8设(X,*,0)是分配对合BCK代数,则(X,≤,')是Boole代数。
证明设X是分配对合BCK代数。对任意x,y∈X,由命题6(5),可令w(x,y)=y*(y*x)=x*(x*y)。则由(P1),(K3)和(K4)知w(x,y)*x=(x*(x*y))*x=(x*x)*(x*y)=0,故w(x,y)≤x,同理可知w(x,y)≤y。
又设t≤x,t≤y。则t*x=t*y=0。又由(P5)得y*x≤y*t,y*(y*t)≤y*(y*x)=w(x,y),而y*(y*t)=t*(t*y)=t*0=t,故t≤w(x,y)。这说明w(x,y)是x,y的下确界,即
x∧y=y*(y*x)=x*(x*y)=w(x,y),
从而(X,≤)为交半格。定义x'=N(x),∀x∈X,则由(P5)知由x≤y可得1*y≤1*x,即y'≤x',于是“'”是逆序对合对应,从而(X,≤,')是有界格且满足De Morgan对偶律。进一步有

由(K3)知x∧x'=x*x=0。于是,(X,≤,')是Boole代数。
由命题7和8立得:
定理2分配对合BCK代数与Boole代数是相互等价的代数系统。
4 结论
本文对BCK代数进行了再研究,证明对合BCK代数与正则FI-代数等价。在对合BCK代数中引入分配性,证明了分配对合BCK代数与Boole代数等价,进一步完善了诸多逻辑代数与Boole代数之间关系的理论研究,同时丰富了多值逻辑理论的发展。

