基于SAOR的Massive MIMO系统信号检测算法
许耀华,尤扬扬,胡梦钰,王 剑
(1.安徽大学电子信息工程学院,合肥,230601;2.上海航天电子技术研究所,上海,201802)
引 言
大规模多输入多输出(Massive multiple input multiple output,Massive MIMO)技术作为一种新型MIMO技术,随着不断增加的天线规模,信号处理算法实现的复杂度也在不断增高,如何降低信号处理算法的复杂度成为Massive MIMO无线通信技术的一大研究课题[1-2]。在信号检测算法中,最小均方误差(Minimum mean square error,MMSE)算法能够取得近似最优的检测性能。然而MMSE算法需要处理复杂的矩阵求逆(W-1)运算,复杂度高达O(K3),K表示系统用户个数。近年来,大量文献[3-10]提出了基于MMSE算法的优化算法,可大致分为近似法和迭代法两类。
近似法是一种先得到W-1的近似值,再判决出发送矢量的信号检测方法。文献[3]和文献[4]提出了将W-1通过诺伊曼级数(Neumann series,NS)展开成多项式的近似方法。对于这种算法,当选取较少的展开项数时,虽然复杂度有所降低,但是检测性能会有所损失。当展开项数大于2时,计算复杂度依然很高,甚至超过了计算W-1的复杂度。文献[5]和文献[6]提出了利用Newton迭代算法近似计算W-1,再恢复原始信号。当迭代次数大于2时,这种算法计算复杂度仍然很高。
文献[7-10]提出了几种基于求解线性方程组的迭代算法,其中,对称逐次超松弛(Symmetric successive over-relaxation,SSOR)迭代算法[10]性能较优。相比于近似法,SSOR迭代算法虽然复杂度始终保持在较低的数量级O(K2)上,但收敛速度较慢,在信道不理想的情况下难以实现理想的检测性能。
针对上述问题,本文将收敛速度较快的SAOR迭代算法[11]应用到Massive MIMO信号检测中,提出了基于SAOR迭代的系统信号检测算法。该算法不直接计算用户发送的信号矢量,而是通过SAOR迭代算法求解线性方程组,逐步得到逼近发送矢量的近似序列,从而避免计算复杂的W-1,大大降低了算法复杂度。本文还给出了SAOR迭代算法的收敛条件、局部最优解、初始值的选取以及复杂度分析。仿真结果表明,通过选取合适的参数和初值,本文提出的检测算法实现了更好的误码率性能,并保证了算法逼近MMSE检测性能的收敛速度。
1 系统模型
本文考虑Massive MIMO系统上行链路。假设xi∈Q是第i个用户发送的符号向量,故K个用户发送的K×1维符号向量可表示为x=[x1,x2,…,xK]T,其中1≤i≤K,Q表示调制字母表。基站端接收到的信号矢量可表示为[3]
式中,n是N×1维加性高斯白噪声向量,且服从CN(0,σ2)分布。H ∈CN×K是信道矩阵,N是基站天线数。
MMSE检测算法[3]就是从基站端天线接收到的信号向量y估计出用户端发送的信号矢量x,得到估计值 x̂为
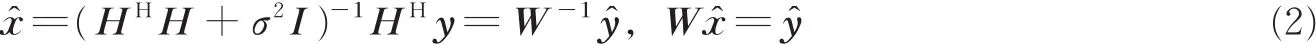
式中,I是单位矩阵,HH是H的对称转置矩阵,ŷ=HHy是y的匹配滤波输出。由式(2)可知

式中,G=HHH是格拉姆矩阵。由文献[3]可知,直接计算W-1的复杂度高达O(K3)。
2 基于SAOR迭代的信号检测算法
2.1 SAOR迭代算法流程
本节将SAOR迭代算法应用到信号检测算法中,通过详尽的算法推导,最终得到了收敛速度较快的基于SAOR检测算法的表达式。
将线性迭代法应用到信号检测中,不需要直接计算出发送信号的精确解,而是通过求解线性方程组得到一个个近似序列来逐步逼近用户发送的信号矢量,避免了计算复杂的W-1,从而达到降低复杂度的目的。首先,将式(2)中的 Wx̂=ŷ转换为一个关于 x̂线性方程 x͂= φ(x̂)。其中,φ(x̂)是 x͂的线性函数,形如:φ(x̂)=Bx̂+f,B和f分别表示的是迭代矩阵和常向量[12]。因此,算法的迭代格式可以表示为

式中 t=0,1,2,… 为迭代次数。考虑线性方程组 Wx̂=ŷ,其中 W=(wij)wijK×K,ŷ=(ŷ1,ŷ2,…,ŷK),wij是W的第j列第i行元素,K则是用户个数,i,j=1,2,…,K,对照式(4)得到迭代格式为

式中xi和ŷi分别表示x和ŷ的第i个元素。观察式(5)可将矩阵W分裂为

(4)改写为

式中迭代矩阵-D-1(U+L)即为Jacobi矩阵[9]。观察式(5),将已计算出的xit+1立即替换掉后续方程中的xit,保证后续方程中执行每次计算时使用的都是最新的数据,从而加快算法的收敛速度。因此可将式(5)改写为
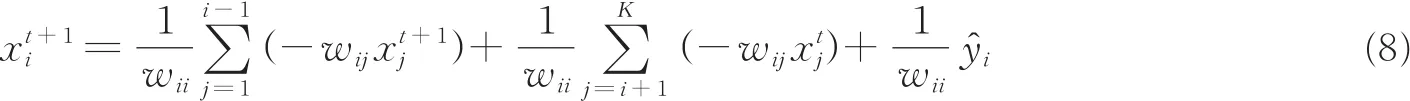
由式(8)可得到矩阵表达式为

为了进一步改善迭代的收敛性和收敛速度,在已求出xt的基础上,仍用式(9)求出xt+1,然后通过加速参数β和松弛参数α将xt和xt+1线性结合,能够得到更好的近似解,从而可以得到
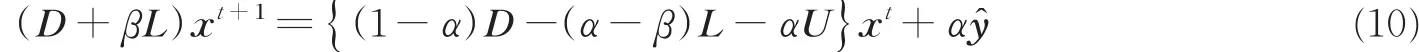
最后,基于切比雪夫加速法[13],将迭代方程式(10)改写为两个半迭代方程,即可得到收敛速度较快的基于SAOR迭代的检测算法表达式:
(1)计算第一个半迭代,就是式(10)本身
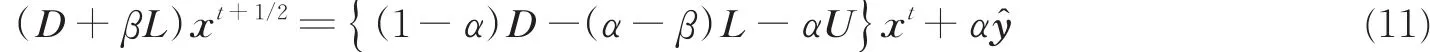
(2)计算第二个半迭代,就是将式(10)中的L和U互换
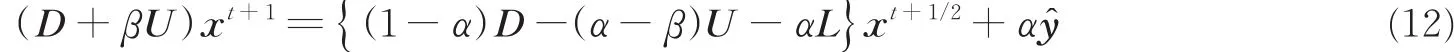
基于SAOR迭代的检测算法每迭代一次,就会进行两次半迭代计算,再次加快了算法收敛速度。此外,在加速参数和松弛参数两个参数的联合加速下,SAOR迭代算法具有更好的精确解和收敛速度。因此,通过选取合适的参数和初值,基于SAOR迭代的信号检测算法在较低的迭代次数时能得到较好的收敛速度和误码率性能。此外,由文献[10]可知,基于SSOR的检测算法是基于SAOR迭代的检测算法在α=β时的特殊情况。基于SAOR迭代的检测算法具体描述如表1所示。

表1 基于SAOR迭代的信号检测算法Table 1 SAOR-based signal detection algorithm
2.2 收敛性分析
对于基站天线数远大于用户数的Massive MIMO系统,实值信道矩阵H具有全列秩的特性[14]。所以对任意K×1维的非零向量q,都有

所以格拉姆矩阵G=HHH是正定矩阵。此外,容易得出

综上,G是对称正定的。由于σ2>0,可得到W=G+σ2I是正定矩阵。由此,文献[15]给出了SAOR迭代算法收敛的条件是

式中,α和β不同时为2。由文献[16]可知,SAOR迭代算法最优的加速参数和松弛参数
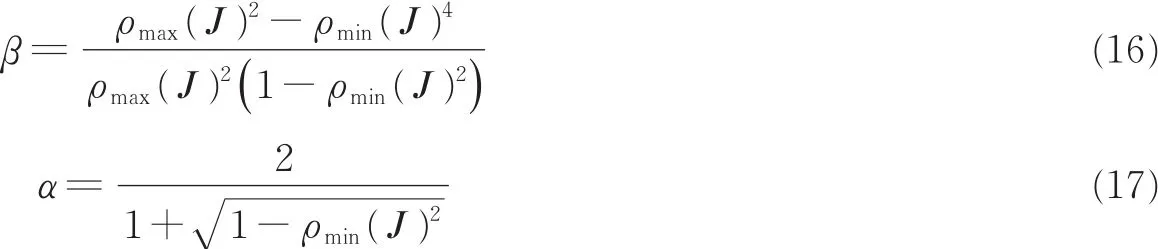
式中ρmin(J)和ρmax(J)分别为Jacobi矩阵的最小和最大特征值。
因此,当加速参数和松弛参数满足式(15)时,本文提出的SAOR检测算法收敛。并且,当参数满足式(16)和(17)给出的条件时,所提算法能够得到全局最优解。
2.3 初始值的选取
传统的迭代算法一般选取零向量作为初始解,初始解会影响迭代的收敛速度,尽管对其收敛性没有影响。所以选取一个合适的初始解会让基于SAOR的检测算法收敛得更快,并且获得更好的检测性能。
基于系统基站天数目远大于用户个数,由文献[14]可以得到

基于Massive MIMO系统信道硬化现象[14],当系统用户数K和基站天线数N足够大,并且当K/N为固定值时,基于SAOR的检测算法初始解向量可选为

2.4 复杂度分析
由于计算复杂度是由乘法器的个数决定的,所以式(11)和式(12)两部分决定了SAOR迭代算法的计算复杂度。
(1)将式(11)改写为
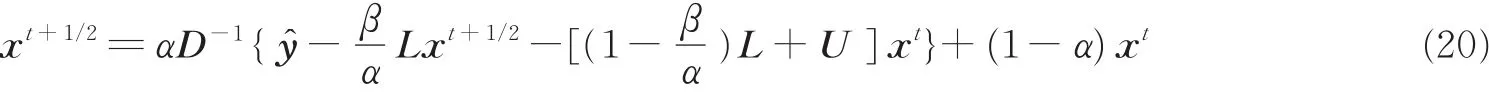
式中
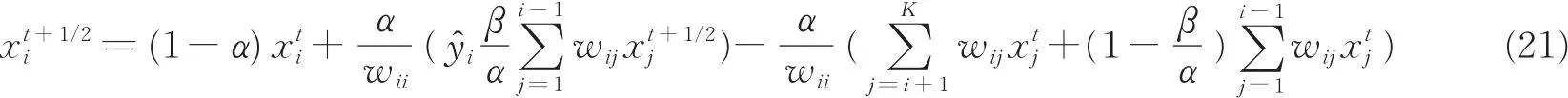
(2)将式(12)改写为
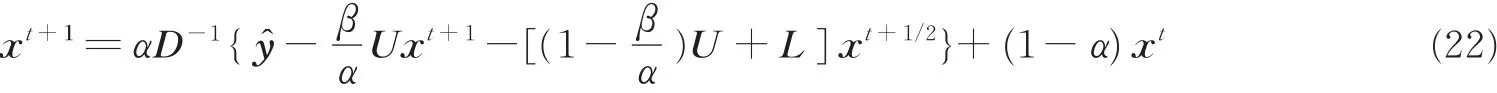
对于所有元素,都有

同理可得,式(12)也需要(3K2+7K)/2个乘法器。
综上,基于SAOR迭代的检测算法总的计算复杂度是t(3K2+7K)。可见,该算法无论进行多少次的迭代运算,复杂度都保持在较低的数量级,为O(K2)。
表1对比了较优的基于SSOR的检测算法、基于NS的检测算法和本文提出的基于SAOR的检测算法三者的复杂度。由表2可看出,当展开项数t≥3时,NS近似算法的计算复杂度依然高达O(K3),甚至超过了MMSE检测算法的复杂度。而相同迭代次数的SSOR检测算法和SAOR检测算法的复杂度相似,始终保持在较低的数量级。但是,SAOR检测算法的检测性能和收敛速度明显优于SSOR检测算法,较快的收敛速度也就意味着较低的复杂度。

表2 计算复杂度比较Table 2 Computational complexity comparison
3 仿真结果
本节给出了Matlab蒙特卡洛仿真结果。仿真参数为:基带信号调制方式是16QAM,天线规模是N×K=128×16。传输信道是瑞利衰落信道,信道特性时变,信道维数128×16。t表示的是各检测算法的迭代次数或展开项数。
基于第2节的算法分析可知,松弛参数α和加速参数β对基于SAOR检测算法的收敛性和收敛速度都起着至关重要的作用。为了得到基于SAOR检测算法误码率(BER)性能的全局最优解,以MMSE检测算法误码率性能为基准,在参数收敛区间(0,2)内对算法的收敛情况进行多次实验。选取的信噪比为8 dB,迭代次数为3。经多次实验得到本次仿真的最优参数为α=1.21,β=1.28。图1给出了当加速参数β分别为0.9,1.28,1.4时,基于SAOR的检测算法误码率随松弛参数α的变化情况。由图1可以看出,随着α的增大,基于SAOR的检测算法的误码率均先减小到一个最小值然后增大,其中β为1.28,α为1.21时,基于SAOR的检测算法得到了全局最优解,其误码率近乎实现了MMSE的检测性能。同样地,由图2可以看出,当α分别为0.9,1.21,1.5时,随着β的增大,SAOR迭代算法的误码率均先减小到一个最小值然后增大。综上,在后续实验中选取α=1.21,β=1.28作为SAOR迭代取得全局最优解时的最优参数。
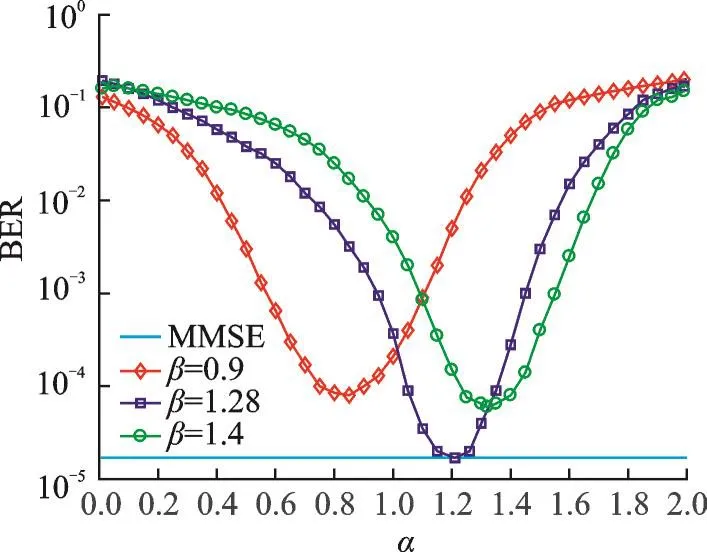
图1 不同松弛参数时误码率对比Fig.1 Comparison of BERs with different relaxation parameters
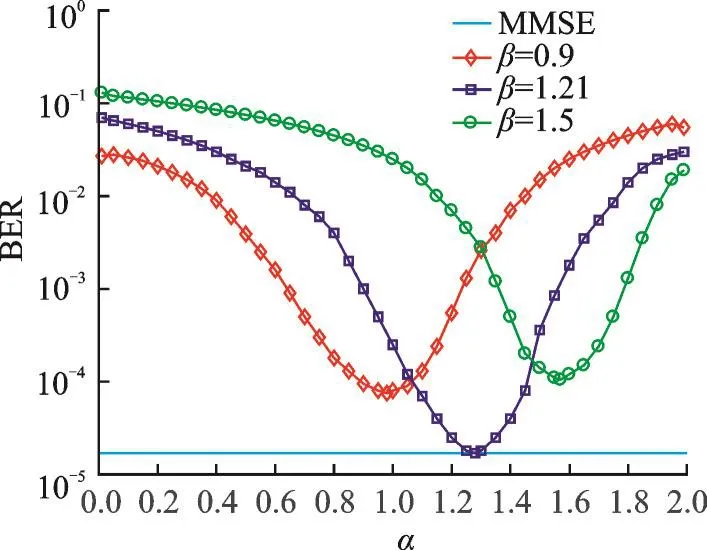
图2 不同加速参数时误码率对比Fig.2 Comparison of BERs with different acceleration parameters
图3 对比了各检测算法在不同信噪比时的误码率性能。由图3可以看出,在相同条件下,基于SAOR的检测算法的误码率性能要优于基于SSOR的迭代算法和基于NS的检测算法。例如,当t为3,信噪比为8 dB时,基于SSOR的检测算法的误码率和基于NS的检测算法的误码率分别约为4.6×10-5和1×10-3,而基于SAOR的检测算法的误码率仅为1.8×10-5。此外,要实现10-5的误码率,SAOR迭代算法所需信噪比要比SSOR迭代算法少约0.9 dB。因此,基于SAOR的检测算法能够以较低的迭代次数获得较优的误码率性能,实现了较快的收敛速度。
图4给出了在信噪比为8 dB的条件下,各检测算法的误码率性能随展开项数或迭代次数t的变化情况,也就是对比了各检测算法逼近MMSE检测性能的收敛速度。由图4可以看出,当基于SAOR的检测算法迭代次数为2时,就已经展现了较好的误码率性能。基于SSOR的检测算法迭代次数为5时和基于NS的检测算法展开项数为7时,能够近似收敛到MMSE算法的检测性能,而基于SAOR的检测算法仅需3次迭代。并且,基于SAOR的检测算法能够实现更接近MMSE的误码率性能。
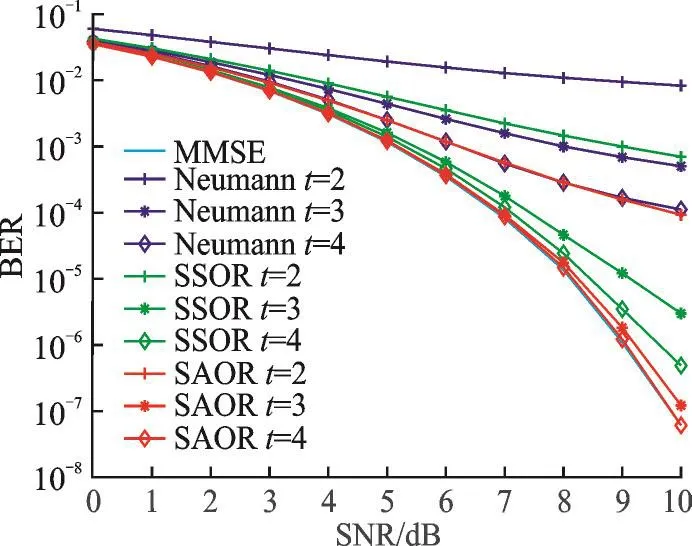
图3 各检测算法误码率对比Fig.3 BER comparison between detection algorithms
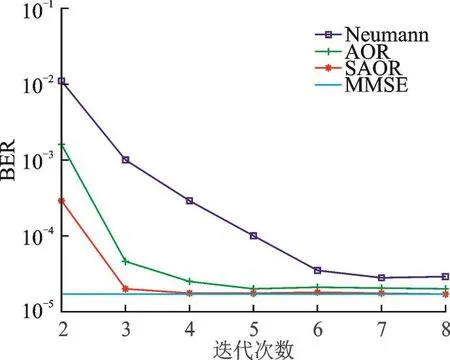
图4 各检测算法收敛速度对比Fig.4 Convergence rate comparison between detection algorithms
因此,通过选取合适的参数和初值,基于SAOR的检测算法的收敛速度和误码率性能都体现出了明显优势。
4 结束语
针对Massive MIMO系统中接近最优的MMSE检测算法复杂度高的问题,本文在信号检测中应用了具有更快收敛速度的SAOR迭代算法。该方法将MMSE检测算法转化为线性方程组并进行迭代计算,求解得到的近似序列能够逐步逼近用户发送的信号矢量,从而避免了复杂的矩阵求逆运算,大大降低了算法复杂度,并且通过选取合适的参数和初值,保证了较快的收敛速度和较好的误码率性能。实验结果表明,本文提出的算法实现了复杂度从O(K3)降到O(K2),并且仅通过3次迭代就能几乎达到MMSE的检测性能,实现了更好的检测性能和更快的收敛速度。下一步考虑将SAOR迭代算法展开到神经网络中,尝试通过训练学习得到更好的信号检测算法。

