双变量“存在性或任意性”问题的解法

■江苏省太仓市明德高级中学

大家知道,逻辑推理的关键要素是：逻辑的起点、推理的形式、结论的表达。而解决双变量“存在性或任意性”问题的关键就是将含有全称量词或存在量词的条件“等价转化”为两个函数值域之间的关系(或两个函数最值之间的关系),下面举例说明,供同学们参考。

一、形如“对任意x1∈A,都存在x2∈B,使得g(x2)=f(x1)成立”问题

例1已知函数f(x)=3x2+2xa(a+2),g(x)=,若对任意x1∈[-1,1],总存在x2∈[0,2],使得f(x1)=g(x2)成立,求实数a的取值范围。

解析：由题意知,g(x)在[0,2]上的值域为

函数f(x)=3x2+2x-a(a+2)的对称轴是x=

当x∈[-1,1]时,函数f(x)的值域为

又由题意可知,当x∈[-1,1]时f(x)的值域是的子集,所以：

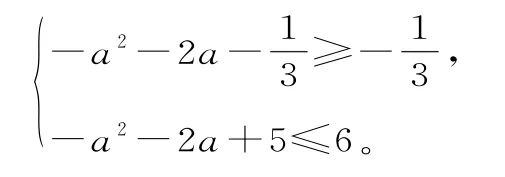
解得实数a的取值范围是[-2,0]。

说明：求解本题的关键是理解全称量词与存在量词的含义,求解此类问题的策略是“等价转化”,即“函数f(x)的值域是g(x)的值域的子集”,从而利用包含关系构建关于a的不等式组,求得参数的取值范围。

二、形如“存在x1∈A及x2∈B,使得f(x1)=g(x2)”问题

例2已知函数f(x)=x2,函数g(x)=若存在x1∈[0,1]及x2∈[0,1],使得f(x1)=g(x2)成立,求实数k的取值范围。

解析：由题意知,函数f(x)的值域为[0,1],g(x)的值域为并且两个值域有公共部分。

先求没有公共部分的情况,即2-2k＞1或

所以要使两个值域有公共部分,k的取值范围是

说明：本类问题的实质是“两函数f(x)与g(x)的值域的交集不为空集”,上述解法的关键是利用了补集思想。另外,若把此种类型中的两个“存在”均改为“任意”,则“等价转化”为利用“f(x)的值域和g(x)的值域相等”来求解参数的取值范围。

三、形如“对任意x1∈A,都存在x2∈B,使得f(x1)≥g(x2)成立”问题

例3已知f(x)=ln(x2+1),g(x)=若对∀x1∈[0,3],∃x2∈[1,2],使得f(x1)≥g(x2),求实数m的取值范围。

解析：当x∈[0,3]时,f(x)min=f(0)=0,当x∈[1,2]时,g(x)min=g(2)=

对∀x1∈[0,3],∃x2∈[1,2]使得f(x1)≥g(x2),等价于f(x)min≥g(x)min。

实数m的取值范围是

说明：理解量词的含义,将原不等式转化为f(x)min≥g(x)min,利用函数的单调性,可求f(x)与g(x)的最小值,从而得到关于m的不等式,便可求得m的取值范围。

四、形如“对任意x1∈A,任意x2∈B,使得f(x1)≥g(x2)恒成立”问题

例4已知函数=2x+a,若f(x1)≥g(x2)恒成立,求实数a的取值范围。

解析：由题意知g(x)max(x∈[2,3])。

因为f(x)在上为减函数,所以f(x)min=f(1)=5。

因为g(x)在[2,3]上为增函数,所以g(x)max=g(3)=8+a。

于是有 5≥8+a,即a≤-3。

所以实数a的取值范围(-∞,-3]。

说明：本题与例3相似,解答的关键也是理解量词的含义,将原不等式转化为f(x)min≥g(x)max。利用函数的单调性,可求f(x)的最小值与g(x)的最大值,从而得到关于a的不等式,便可求得a的取值范围。