复数考查有思路 三条主线帮你学

■福建省德化第一中学

复数是近几年来高考全国卷与各地市自主命题必考的一个知识点,考题一般设置在试卷的前面,难度不大。复数是初等数学与高等数学的衔接点,相关概念较多,理解概念是解决复数问题的基础。本人通过研究近几年全国各地的高考复数题,总结出复数考查的三条主线,帮助同学们学习。

主线一：通过复数运算获得复数代数形式z=a+bi(a,b∈R),再利用其相关概念、性质进行求解。

复数的运算包括：

复数的加法运算：(a+bi)+(c+di)=(a+c)+(b+d)i；

复数的减法运算：(a+bi)-(c+di)=(a-c)+(b-d)i；

复数的乘法运算：(a+bi)(c+di)=(ac-bd)+(ad+bc)i；

复数的除法运算：(a+bi)÷(c+di)=

复数的性质包括：复数的模、实部、虚部、共轭复数,复数所对应点的坐标等内容。

例1(2019年全国Ⅰ卷文数第1题)设则|z|=( )。

解析：通过复数运算,化简得所以

例2(2014年湖南卷)复数为虚数单位)的实部等于_____。

解析：通过复数运算,化简得z=-3-i,所以实部为-3。

例3(2019年江苏卷)已知复数(a+2i)(1+i)的实部为0,其中i为虚数单位,则实数a的值是____。

解析：由题意知(a+2i)(1+i)=(a-2)+(a+2)i,复数的实部为0,则a-2=0,a=2。

例4(2019年全国Ⅱ卷)设z=i(2+i),则

A.1+2i B.-1+2i

C.1-2i D.-1-2i

解析：z=i(2+i)=-1+2i,它的共轭复数为-1-2i,故选D。

例5(2017年北京卷理科数学)若复数(1-i)(a+i)在复平面内对应的点在第二象限,则实数a的取值范围是( )。

A.(-∞,1) B.(-∞,-1)

C.(1,+∞) D.(-1,+∞)

解析：z=(1-i)(a+i)=(a+1)+(1-a)i。因为对应的点在第二象限,所以有解得a＜-1,故选B。

例6(2019年全国Ⅱ卷理数)设z=-3+2i,则在复平面内对应的点位于( )。

A.第一象限 B.第二象限

C.第三象限 D.第四象限

解析：计算得=-3-2i,其对应点的坐标为(-3,-2),在第三象限,故选C。

以上例题均可通过复数运算,化简获得z=a+bi(a,b∈R)这种代数形式,再利用相关概念如实部、虚部、共轭复数、模等进行解题。

主线二：通过求解复数方程,获得复数的代数形式z=a+bi(a,b∈R),再利用其相关概念、性质进行求解。

例7(2019年全国Ⅲ卷理数)若z(1+i)=2i,则z=( )。

A.-1-i B.-1+i

C.1-i D.1+i

解析：利用方程的思想,求得1+i,选D。

变式：(2017年新课标Ⅲ卷理数)若复数z满足z(1+i)=2i(i为虚数单位),则|z|=( )。

解析：利用方程的思想,求得1+i,则选C。

例8(2019年上海卷)设i为虚数单位,3z-i=6+5i,则|z|=( )。

解析：解复数方程,可将z看成一个未知数,通过解方程求出z即可,解得3z=6+6i,z=2+2i,|z|=,选B。

例9(2015年江苏卷)设复数z满足z2=3+4i(i为虚数单位),则z的模是____。

解析：可设z=a+bi(a,b∈R),再利用两复数相等,实部相等且虚部相等获得a,b的值。

(a+bi)2=3+4i,a2-b2+2abi=3+4i。

z=2+i或z=-2-i,则z的模为

例10(2015年山东卷)若复数z满足其中i为虚数单位,则z=( )。

A.1-i B.1+i

C.-1-i D.-1+i

解析=i(1-i)=1+i,所以z=1-i,选A。

例11(2015年全国Ⅱ卷)若a为实数,则a=( )。

A.-4 B.-3 C.3 D.4

解析,得2+ai=2+4i,a=4,故选D。

例12(2014年江西卷理数)设是z的共轭复数,若=2(i为虚数单位),则z=( )。

A.1+i B.-1-i

C.-1+i D.1-i

解析：(法一)由得2z=2-2i,则z=1-i,选D。

(法二)设z=a+bi(a,b∈R),由a+bi+a-bi=2,得a=1；由(a+bi-a+bi)i=2,2bi2=2,得b=-1,z=1-i。故选D。

例13(2013年广东卷)若i(x+yi)=3+4i,x,y∈R,则x+yi的模( )。

A.2 B.3 C.4 D.5

解析：(法一)设z=x+yi(x,y∈R),由iz=3+4i,得,选D。

(法二)ix+yi2=3+4i,则-y+xi=3+4i,y=-3,x=4。故4-3i的模为5,选D。

以上例题均可通过方程或方程组的思想求解,获得复数z=a+bi(a,b∈R)的代数形式,再利用相关概念如实部、虚部、共轭复数、模等进行解题,这也是求解复数问题的重要途径之一。

主线三：复数与其他知识交汇求解问题。

复数的问题主要是按以上两条主线进行考查的,有时也会涉及一些交汇型问题,即把复数知识与其他的代数、几何知识有机地结合起来,就是在复数的运算法则等基础上添加其他元素设计问题进行考查。

例14(2019年全国Ⅰ卷理数)设复数z满足|z-i|=1,z在复平面内对应的点为(x,y),则( )。

A.(x+1)2+y2=1

B.(x-1)2+y2=1

C.x2+(y-1)2=1

D.x2+(y+1)2=1

解析：由|z-i|=1,得其为以(0,1)为圆心,1为半径的圆,故答案为C。

本题考查的是复数模的几何意义,即复数模为复数z在复平面上对应的点到定点的距离。

例15(2015年陕西卷理数)设复数z=(x-1)+yi(x,y∈R),若|z|≤1,则y≥x的概率是( )。

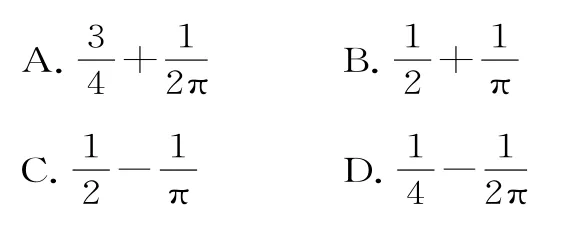
解析：先根据|z|≤1得(x-1)2+y2≤1,这是一个以(1,0)为圆心,1为半径的圆及其内部,再通过数形结合,用几何概型的概率求解即可,选D。

例16(2013年湖北卷)i是虚数单位,设z1,z2在复平面内对应点关于原点对称,若z1=2-3i,则z2=____。

解析：z1=2-3i在复平面内对应点为(2,-3),点(2,-3)关于原点对称的点的坐标为(-2,3),所以z2=-2+3i。

本题考查了复数对应复平面内的点,再结合对称这个考点进行问题的设计。

例14、15、16主要是借助复数的几何意义,考查复数z对应复平面内的点的位置或点的轨迹,同时结合图形的面积与概率知识,考查数形结合思想的应用。

例17(2015年福建卷)若集合A=｛i,i2,i3,i4｝(i为虚数单位),B=｛-1,1｝,则A∩B等于( )。

A.{-1} B.{1}

C.{1,-1} D.∅

解析：本题是复数与集合的交汇,通过计算中A元素i,i2,i3,i4可得A=｛i,-1,-i,1｝,进而A∩B=｛-1,1｝,故选C。

例18(2017年全国Ⅰ卷理数)设有下面四个命题：

p1：若复数z满足,则z∈R；

p2：若复数z满足z2∈R,则z∈R；

p3：若复数z1,z2满足z1z2∈R,则z1=

p4：若复数z∈R,则¯z∈R。

其中的真命题为( )。

A.p1,p3B.p1,p4

C.p2,p3D.p2,p4

解析：本题是复数与命题知识的交汇,要理解复数的基本概念,利用复数的代数形式z=x+yi(x,y∈R)即可计算的代数形式,进而判断命题的正误,选B。

例19(2014年陕西卷理数)原命题为“z1,z2互为共轭复数,则|z1|=|z2|,关于其逆命题,否命题,逆否命题的真假判断依次如下,正确的是( )。

A.真假真 B.假假真

C.真真假 D.假假假

解析：解题过程略,选B。

例20(2015浙江)已知i是设虚数单位,a,b∈R,则“a=b=1是(a+bi)2=2i”的____。

解析：由a=b=1可推得(a+bi)2=2i,而(a+bi)2=2i却有ab=1且|a|=|b|,则“a=b=1是(a+bi)2=2i”的充分不必要条件。

例17、18、19与例20则是考查复数的概念与集合、命题的交汇,主要是借助复数的概念考查命题的四种情况、真假性以及充要条件等基本知识。

结语：考查复数内容的思路较直观,命题者主要是根据以上三种思路进行问题的设计,通过以上一些复数高考题的呈现,同学们在学习的过程中,能够做到“知己知彼”、对本节知识“胸有成竹”,同时可适当结合其他知识点进行求解,这样学习才能高效。