近58 年马鞍山市降水量变化规律分析
邢寿文
(安徽省马鞍山水文水资源局,安徽 马鞍山 243000)
0 引言
进入21 世纪,全球变暖日益明显,区域极端天气灾害频繁[1~3]。暴雨作为一种极端天气,给城市人民财产和生命带来了极大的危害,关于暴雨预报、由暴雨引起的洪水灾害评估已经成为当下研究的热点问题[4~5]。马鞍山是中国东部安徽省的一个地级市。它是一个横跨长江的城市。马鞍山河流较多,主要包括扬子江的马鞍山河段、采石河、玉山河、磁湖河、玉山湖和索溪河,因此水资源较为充沛。受自然地理,气候,人类活动和工程条件的影响,马鞍山地区的洪水频繁发生,暴雨持续时间短,范围广,位于该省年平均降水量的高值区域。本文以马鞍山以及周边气象站的月值降水数据为基础。利用小波分析,对过去58年降水的时间- 周期趋势进行分析,为该地区防洪减灾提供理论参考。
1 资料与方法
1.1 资料来源与数据处理
本文利用马鞍山及周边地区四个气象站的月降水观测资料(来自中国气象科学数据共享服务网)。将四个气象站数据进行平均处理,代表马鞍山的年平均降水量。分析了地区降水的时空变化特征,研究期为1961 年~2018 年。从统计学角度说,相对长的时间序列能够保证研究区域分析结果的可靠性。
1.2 研究方法
本研究采用趋势分析法、Mann-Kendall 检验法以及小波分析法对马鞍山降水变化趋势以及规律进行分析。为分析径流量的变化趋势,本文采用倾向率方法进行分析,即建立径流量与时间的一元线性回归方程,来反映径流量的变化趋势。本文以近58 a 的降水数据为基础,对其进行非参数检验,以反映马鞍山降水的变化趋势。最后通过小波分析对研究区内降水周期变化进行研究。
(1)Mann-Kendall 检测法
Mann-Kendall 检验法是一种非参数统计检验方法,用于预测各种观测要素的时间序列数据的长期趋势。Mann-Kendall 检验中,原假设H0为原序列(x1,x2,…,xn)无变化趋势,备择假设H1为双边检验,构造秩序列Sk:

式中:
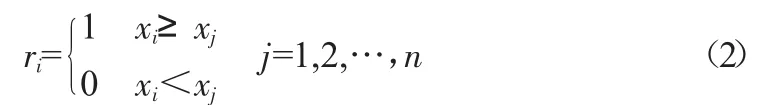
定义统计变量:
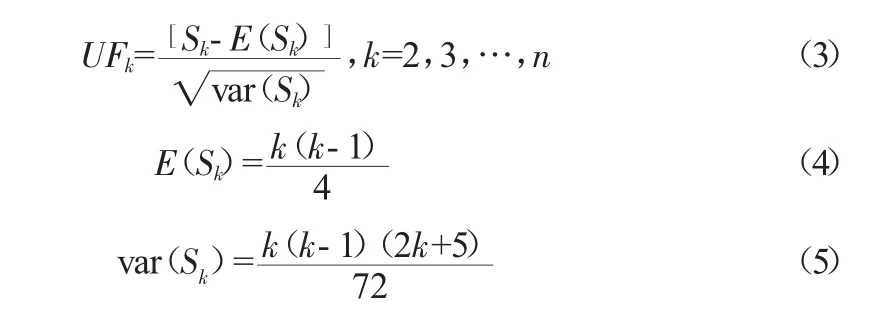
UFk为标准正态分布,对于给定显著性水平α,若UFk>Uα/2,则表明原序列存在明显的趋势变化。将时间序列逆序排列为xn,重复相同的操作,得到UBk,满足UBk=-UFk(k=1,2,…,n)。通过UFk和UBk的曲线走势可分析序列x 的变化趋势。当两条曲线相交,则为突变时刻。
(2)小波分析法
针对水文数据的特征,本文选用Morlet 小波作为小波函数φ(t),时间序列f(t)的小波变换为:

其中:Wf(a,b)称为小波变换或小波系数(t)为复共轭函数;a>0 为尺度因子,反映了小波周期长度;b 为时间因子,反映了在时间上的平移。Wf(a,b)反随a 和b 变化,可做a 为横坐标、b为纵坐标的等值线图。此图可反映随时间变化的小波特征。不同时间尺度下的小波系数可以反映系统在该周期下的变化特征。φ(t)可以取不同形式,Morlet 小波的变换形式为:

小波方差由下式表示,可用来确定主周期:

2 降水量时间变化特征分析
2.1 年降水量变化分析
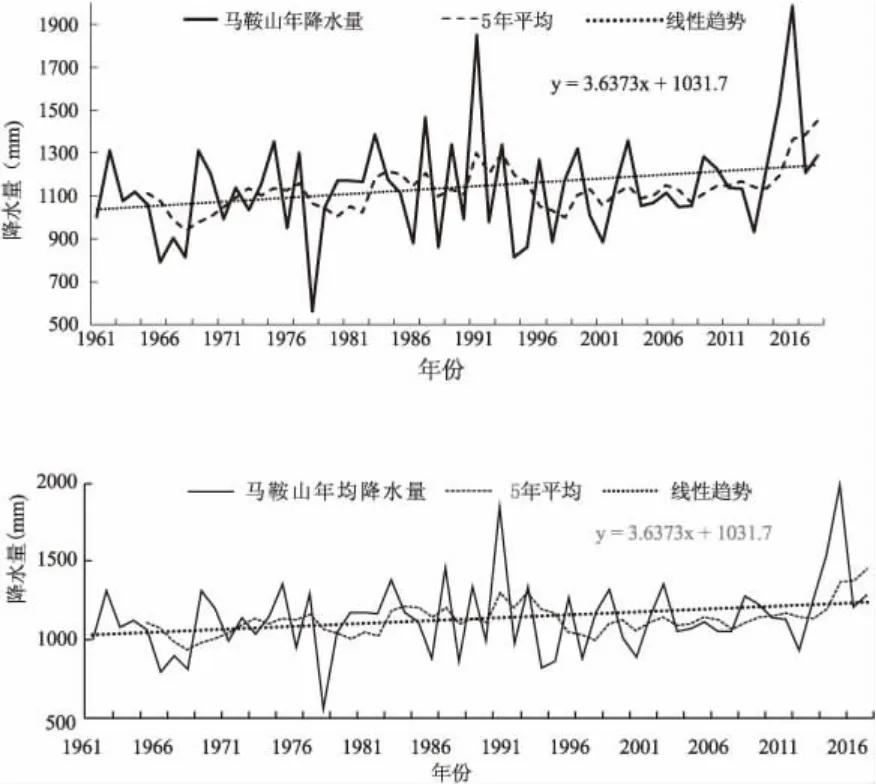
图1 马鞍山近58 年降水量变化趋势
马鞍山多年平均降水量为1139 mm,且整体处于上升趋势,降水变化倾向率为3.6373 mm/a,由于季风的影响,该地区的降水量在年内和年际变化很大,这使得该区域经常有集中的大雨和交替的干旱和洪水。6 月份以后,进入东南季风控制时期,暴雨由南向北逐渐增多,7 月~8 月份是频发时期,占暴雨次数的63%~68%,这是7 月份最多,占38%~45%,并在9 月中旬后逐渐减少,最后在10 月份逐渐减少。暴雨持续日数,一般为1 天~2 天,最长3 天。暴雨与洪水密切相关,暴雨的强度和总量决定了洪水的严重程度。该地区的暴雨持续时间短,强度大,范围广,是安徽省年平均降水量的高值区域。
2.2 降水量季节变化特征分析

表1 降水季节变化特征
由于处于亚热带季风气候区,夏季受来自海洋的暖湿夏季风影响,降水明显增多,流域内降水季节性变化明显。由表1 可知,降水主要集中在夏季,平均降水量为688.0 mm,占年降水量的60.4%。其次是春季和秋季,降水量分别为184.5 mm 和203.9 mm,占年降水量的16.2%。17.9%,而冬季降水量仅为61.5 mm,约占年降水量的5.4%。从降水变化率来看,春、秋季降水变化率为负值,分别为-3.7 mm/10 a 和-3.1 mm/10 a,夏、冬季降水变化率为正值,分别为2.4 mm/10 a、和0.4 mm/10 a。
2.3 年降水量M-K 检验
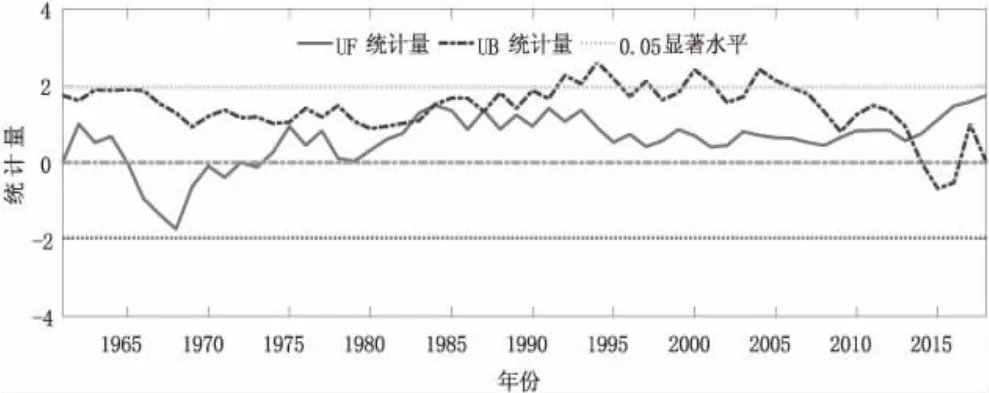
图2 马鞍山近58 年降水量突变检验
图2 为马鞍山降水量突变检验图,从图中可以看出,在研究时间范围内有多个突变点,主要发生在1975 年、1982 年、1984 年、1987 年和2014 年左右,且都在0.05 置信区间范围以内,说明降水量振荡变化明显,尤其是在20 世纪80 年代发生多次突变,振荡最为强烈,到90 年代降水量整体呈现减少趋势,然后维持在一个水平,在2010 年以后开始大幅增长。
3 降水量时间周期分析
为了进一步研究地区年降水量的时间推移趋势,对马鞍山近58年的降水进行了小波分析。采用MATLAB 进行绘制,结果见图3~图6。
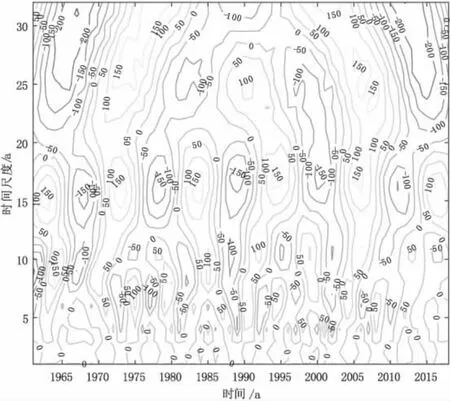
图3 马鞍山年降水量小波实部等值线图
选定的数据是由年平均降水量(1961 年~2018 年)表示的平面,其中,横坐标为时间,纵坐标为时间尺度,图中的等值曲线为小波系数实部值。当小波系数实部值为正时,代表降水量的丰水期;为负时,表示降水量的枯水期。因此小波变换系数的实部在平面轮廓上的正负值是在时域上反映了降水降水量的枯丰交替的变化,反过来,可以判断不同时间尺度的年降水量的未来趋势[3]。
从图3 中,我们可以清楚地看到58 a 年降水量演变中存在的多时间尺度特征。不同尺度的正相和负相之间振荡中心的形成具有明显的年际和年代际变化。总的来说,在降水演变过程中,有三种类型的周期性变化模式,分别为3 a~8 a,13 a~20 a和22 a~32 a。其中,年降水量有两个准振荡周期,在22 a~32 a范围内。1984 年~1995 年及2006 年以后为枯水年,1973 年~1983 年及1996 年~2005 年为丰水年。13 a~20 a 的年际变化尺度存在枯丰交替5 次周期振荡,周期连续性最为完整;3 a~8 a 的年际变化尺度没有全局性。
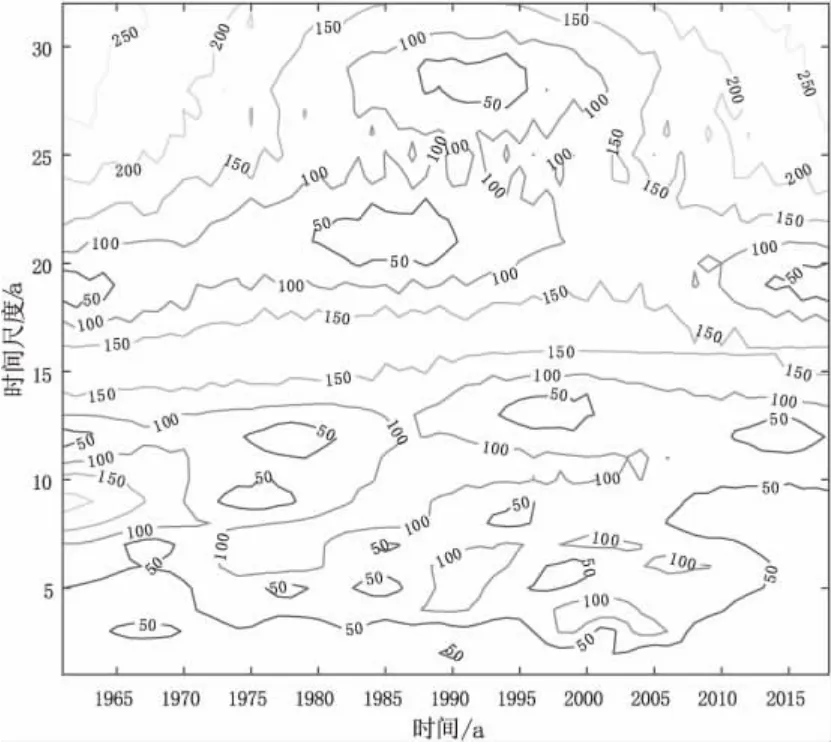
图4 模等值线图
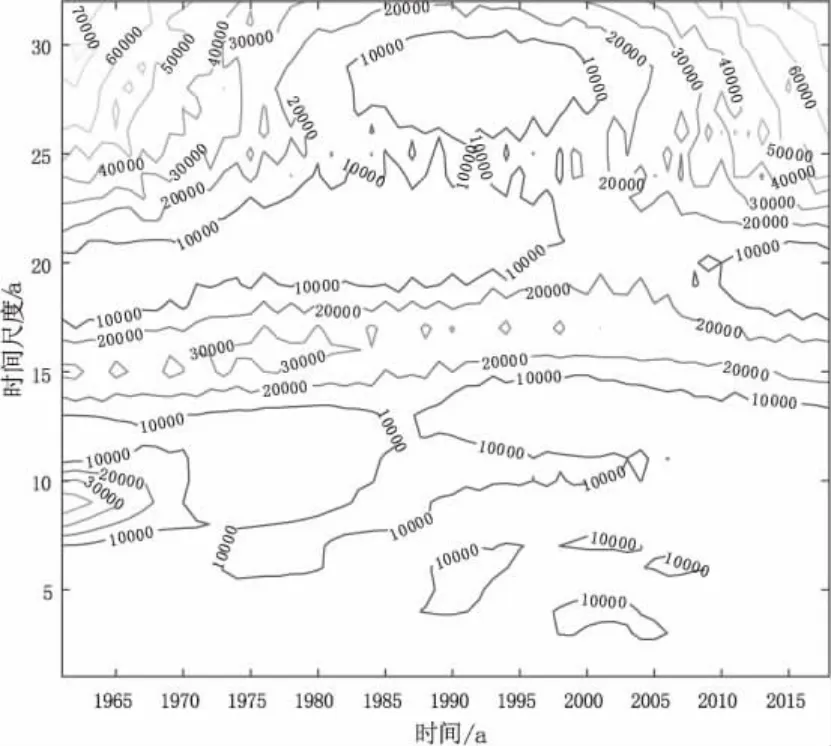
图5 模方等值线图
从小波变换系数模值和模值的平方等值线图可以看出(图4 和图5),地区22 a~32 a 尺度的周期变化最为明显。但其周期性变化具有局部化特征,不具有全域性,从图中可以看出此时间尺度在两端时间区域内周期性较强,其他时间段较弱,能量较低,能量先趋向下降然后随时间增加。其次,13 a~20 a尺度的周期变化也很明显,具有全球性。时间尺度3 a~8 a具有最差的周期性,弱能量和不均匀分布,也没有全局性。在3 a~8 a 尺度中模值最高值出现在1973 a~2010 a,此时段周期性较强,能量值与其他时间段相比也最大。
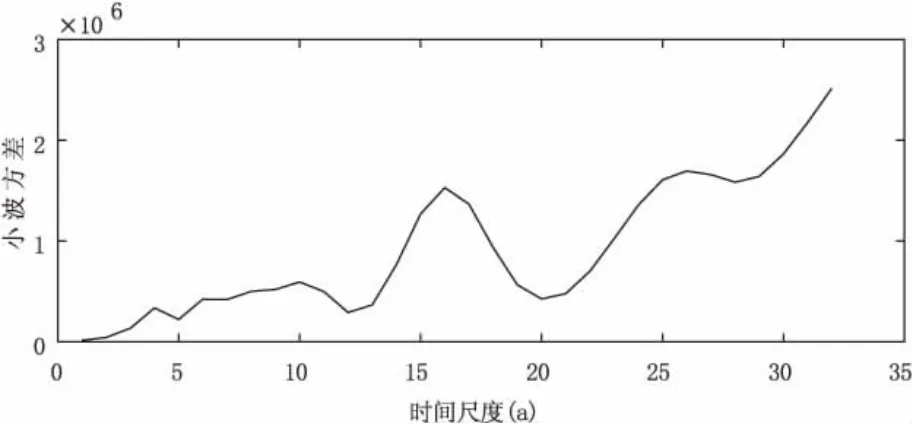
图6 小波方差图
小波方差图可以用时间尺度反映降水时间序列的波动能量分布,小波方差随尺度的变化而变化。该过程可以反映时间序列中包含的各种尺度(周期)的特征以及它们作为比例函数的优缺点(能量大小)。因此,通过小波方差图(即降水过程中存在的主要周期)找到时间序列中的主要尺度(周期)非常方便。
研究区域降水的小波方差图有两个不同的峰值(图6),分别对应于26 年和16 年的时间尺度,并且在整个研究时间范围内可测量时标的最大值对应于32 年时标。因此马鞍山年降水量变化的第一个主要周期为32 年;26 年的时间尺度对应于第二个峰值,这是降水量变化的第二个主要时期。这表明上述三个周期的波动决定了整个时域降水量的变化特征。
4 结论
(1)受季风影响,马鞍山年内降水量变化较大。处于安徽省多年平均降水量的高值区,6 月份以后,进入东南季风控制时期,暴雨由南向北逐渐增多,7 至8 月份是频发时期,占暴雨次数的63%~68%,9 月中旬后逐渐减少。
(2)马鞍山春、秋季平均降水变化率为负,夏、冬季平均降水变化率为正。分别为-3.7 mm/10 a、-3.1 mm/10 a,2.4 mm/10 a和0.4 mm/10 a,降水变化趋势在不同季节有很大差异,整体呈增长趋势。
(3)马鞍山降水演变中有3 a~8 a,13 a~20 a 和22 a~32 a三种周期性变化。其中22 a~32 a 尺度的周期变化最明显。13 a~20 a 的周期性变化是第二个,3 a~8 a 尺度的周期性最差,能量较弱,分布不均匀;马鞍山降水量分别存在32 a、26 a、16 a这3 个时间尺度周期,其中32 a 是该地区年降水量变化的第一个主要时期;26 a 和16 a 分别为降水变化的第二和三主周期;方差的三个峰值都在3 类时间尺度范围内,也说明了小波变换分析的准确性。

