红壤坡地耕作措施对土壤入渗过程的影响机制
王 移,曹龙熹,樊剑波,任 平
(1.四川师范大学西南土地资源评价与监测教育部重点实验室,四川成都610066; 2.成都理工大学地球科学学院,四川成都610059;3.中国科学院南京土壤研究所,江苏南京210008;
南方红壤区有4 335万亩(289万 hm2)坡耕地,发生在坡耕地上的水土流失占区域流失总量的40%以上[1],也是导致土壤养分流失和肥力退化的主要因素.另一方面,以季节性干旱为代表的土壤水分季节分配不均的问题严重制约了耕地生产力的提高.因此,有必要采取合理的耕作措施以提高红壤坡耕地土壤入渗能力,减弱雨季坡耕地地表产流和水土流失强度,同时也提高旱季土壤涵养水源的能力.
土壤水分入渗是水分通过地表向下流动进入土壤的运动和再分布过程,受到土壤理化性质、土地利用方式、土壤下垫面条件等多种因素的控制[2-3].其中土壤性质是影响入渗能力的重要方面,土壤有机质含量、团聚体和土壤结构等因素都与土壤入渗能力密切相关[4-5].土壤属性在很大程度上受到人类活动的影响,人类活动作用于土壤中生物和理化过程,从而改变土壤有机质、养分含量、容重、孔隙度、初始含水量、团聚体结构等指标[6].国内外学者已对不同利用方式下的土壤理化性质变化和入渗性能的响应进行了大量的研究[7-10].在南方红壤区,学者们也针对农地、林地和草地等不同利用方式研究了土壤入渗能力以及影响因素[11-13],对于农地来说,耕作措施和管理方式是决定土壤入渗过程的关键方面,而目前红壤区针对耕作措施影响土壤入渗的机制研究仍相对较为薄弱,特别是多种措施的过程对比和效益评价研究不足.
研究土壤入渗机制需要开展野外或室内模拟试验,如模拟降雨法、双环入渗法或者环刀法等[14],其中双环入渗法因其原理简单、扰动较小且能反映野外实际条件,被国内外很多学者用来研究土壤入渗过程和测定入渗参数[15-17].在获取土壤入渗过程数据的基础上可以构建数理模型进行趋势拟合和参数量化[7],代表性的土壤入渗模型有Horton 模型[18]、Kostiakov 模型[19]和 Philip 模型[20]等.学者们研究发现不同试验方法测定结果适宜的入渗数理模型各不相同[16],甚至同一种土壤在不同季节入渗曲线的拟合模型也存在差异[21],这体现了土壤入渗的复杂机制,也说明了开展不同条件下土壤入渗能力对比量化研究的必要性.
本文以典型红壤坡耕地为研究对象,布设以花生为主的5种种植措施,基于田间小区长期试验样地探究耕作措施对土壤理化性质的影响程度和方式,并通过野外双环入渗试验获取土壤入渗过程参数,在此基础上分析耕作措施对土壤入渗的影响机制,提出用于研究区坡耕地土壤入渗评价的方法,从而为红壤坡地耕作措施的优化布设提供理论依据.
1 研究方案
1.1 研究区概况 本研究试验布设在中国科学院红壤生态试验站,位于江西省鹰潭市余江县内(28°15′20″N,116°55′30″E),西距南昌市 135 km,东距鹰潭市13 km,该站地处江西省东北山区向潘阳湖平原过渡地带,地势变化平缓,以低丘和岗地为主,海拔均在100 m左右,属于中亚热带湿润季风气候,四季分明,年平均气温17.6℃,年降雨量1 785 mm,但季节分布不均,降雨50%集中于每年的3月至6月,年均日照时数为1 852.4 h,年蒸发量1 378 mm,具有明显的干湿季节变化、夏、秋之间旱情突出,无霜期为262 d.研究区常见植被有常绿阔叶林、落叶阔叶林及针叶林,覆盖率约为45%.成土母质以第四纪红色黏土、泥质页岩、花岗岩为主,土壤类型为红壤和红壤性水稻土,适用于农林牧生产,主要农作物为玉米、水稻、油菜、柑橘和花生等,一年两至三熟.土地利用方式以林荒地为主,坡耕地次之,水田较少.由于该区人口密度大,丘陵坡地利用率高,雨量丰富且雨热同期,加之土壤自然风化度程度高、肥力水平低、黏粒含量高,具有易板结、易侵蚀等特点,主要水蚀类型为面蚀和沟蚀,并以面蚀为主[22-23].
1.2 试验样地设置 花生是当地旱作的主要经济作物,本研究在考虑当地传统耕作措施的基础上,以花生为主要作物设置了5个处理,分别为:1)传统花生顺坡垄作;2)花生+萝卜轮作;3)花生+秸秆覆盖;4)花生+有机肥;5)花生+柑橘套作.除传统顺坡外,其他几种处理的花生均为横坡垄作,耕作措施详见表1.每个处理设置3个重复,共15个小区样地,于2012年布设在中科院红壤生态试验站站区西侧,小区间距大于1 m,使用1 m×1 m的水泥板与周围地区隔开,水泥板露出地表20 cm,埋在地下80 cm,其中柑橘套作小区为20 m×10 m;其余小区为20 m×5 m.
1.3 土壤样品采集与指标测定 在每个实验小区按照“S”形五点法采集0~20 cm土层混合样,用四分法收集1 kg左右的样品,除去砾石、草根等杂物,风干、过筛后备用.同时使用环刀法采集土样测定容重、土壤孔隙度、土壤含水量等指标.采集团聚体指标样品时,为保证田间原状土壤结构不被破坏,需在田间采集大土块,用硬质铝盒承装至实验室,风干至合适含水量后沿自然破裂面小心掰开储藏备用.土壤有机质采用重铬酸钾硫酸消煮法,土壤质地分析用吸管法;采用湿筛-Yord改进法测定水稳性团聚体指标,并计算不同耕作措施土壤的平均重量直径(MWD,mean weigh diameter),团聚体分散度(PAD,percentage of aggregate disruption),包含>0.25 mm 团聚体分散度(PAD0.25)和 >2 mm团聚体分散度(PAD2),水稳性团聚体百分含量(WSA,water stable aggregate),常用的指标有 >0.25 mm水稳性团聚体百分含量(WSA0.25).

表1 不同耕作措施径流小区基本特征Tab.1 Basic characteristics of runoff plot
考虑到在土壤含水量较低的条件下可以获取变幅较大的入渗曲线,于花生收获后的9月份即旱季在小区开展双环入渗试验.入渗试验装置采用特制的双环,其中内环直径为35.5 cm,外环为55.5 cm,环壁高为25 cm,内环用于入渗试验,外环主要是防止内环入渗时可能发生的侧向渗漏.试验时内环和外环打入土的深度均为15 cm,两环的积水深度均为5 cm,试验采取快速人工加水[24].试验前期入渗速率较快,按圆环内水位下降1 cm计时,根据入渗所需的时间计算入渗速率,试验后期入渗速率逐渐减小,在试验进行到60 min后改为记录5 min内的内环水位下降深度,试验结束时间统一为90 min,在这一时间内各处理的入渗速率基本都达到稳定,即连续5次测定的入渗速率大致相同.根据记录的入渗过程数据计算初始入渗速率(试验开始5 min内的入渗速率平均值)、稳定入渗速率(试验结束前5次入渗速率平均值)和平均入渗速率(每次试验的总耗水量除以试验时间),入渗试验在每个小区进行2次重复,共进行30次试验.
1.4 入渗模型与数理分析方法 为了准确量化土壤入渗过程,结合国内外已有土壤入渗机制研究结果,选取具有较好代表性的Horton方程、Philip方程和Kostiakov方程来模拟不同耕作措施的水分入渗过程.
1)Philip方程

其中,f(t)为入渗速率(mm/min),s为吸渗率(cm/min),t为入渗时间(min),fc为稳渗速率(mm/min).
2)Horton公式

其中,f1为初渗速率(mm/min),k为试验求得的参数.
3)Kostiakov方程

其中,y为土壤入渗率(mm/min),x为土壤入渗时间(min),a为经验入渗常数,代表一个单位时段内平均入渗速率,b值的大小则反映土壤入渗速率递减状况,其值越大,表明入渗速率随时间递减的越快[25].
采用 Nash 等[26]提出的模型有效系数(Ef)对比不同入渗模型的拟合精度,模型效率系数反映的是计算值与实测值1∶1线的接近程度,其取值范围为 -∞ ~1.如果模型效率系数接近1,表示模型计算值与实测值非常接近,也就是模型的有效性好,反之,表示模型的有效性较差.
使用单因素方差分析和相关分析方法探讨土壤性质差异及其与入渗参数之间的关系,采用主成分分析方法评价不同耕作措施的综合入渗能力,所有的数理分析和作图在EXCEL 2010、SPSS 21.0和Origin 8.1软件中完成.
2 结果与分析
2.1 不同耕作措施的土壤性质和入渗速率 测定5种耕作措施的土壤理化性质见表(表2).土壤容重在1.20~1.25 g/cm3之间变动,平均值为1.22 g/cm3.受季节性干旱的影响,土壤初始含水量普遍较低.不同耕作措施表层土壤的有机质含量差异显著(ANOVA,P=0.03),套作的有机质含量最高,顺坡的有机质含量最低,这是由于桔树套作增加了土壤中的微生物种类和数量,枯枝落叶、秸秆和有机肥的进一步分解都有利于增加土壤中的有机质含量[27-28].土壤团聚体指标在不同措施之间差异也较大,套作和覆盖的MWD和WSA0.25含量显著高于顺坡和轮作,这2种措施的PAD0.25与PAD2的百分含量则小于顺坡和轮作处理,研究表明MWD与WSA0.25含量越大、PAD0.25与 PAD2的含量越小越有利于水分入渗和防止土壤侵蚀[29],说明套作和覆盖相比于顺坡和轮作可以改善土壤结构,从而提高保水固土效益.本研究有机肥措施的团聚体指标相对较差,其对土壤结构的作用还需要进一步探讨.

表2 不同耕作措施的土壤理化性质Tabl.2 Basic soil physical and chemical properties of different tillage practices
2.2 不同耕作措施的入渗速率及其影响因素 田间双环入渗实验测得不同耕作措施的初渗率、稳渗率和平均入渗率见表3,各指标之间的大小排序为:初渗率>平均入渗率>稳渗率,3种入渗速率在不同处理之间均有显著差异性.初渗率和平均入渗率排序均表现为:套作>有机肥>覆盖>轮作>顺坡;5种耕作措施在90 min的入渗过程中用水量也存在显著差异.套作措施的稳渗率(4.56 mm/min)最大,入渗过程中的用水量(44.05 cm)也最多.秸秆覆盖和有机肥与顺坡和轮作的稳渗率之间没有显著差异,但入渗总用水量则显著偏大,说明这2种措施土壤涵养水分的能力明显提升.本研究顺坡的稳渗率(2.76 mm/min)与吕殿青等[13]采用相同方法在红壤坡耕地条件下的测定结果(2.58 mm/min)十分接近,说明本试验结果具有较好的可靠性.

表3 不同耕作措施入渗速率及用水量对比Tabl.3 Infiltration parameters of different tillage practices
分析水分入渗速率和土壤理化性质的相关性见表4,土壤容重与稳渗率呈负相关,容重越大说明土壤板结严重,土壤孔隙较小,不利于水分的下渗.一般认为土壤前期含水量越大,入渗速率越慢.本研究分析结果为土壤前期含水量与初渗速率和平均入渗率均呈显著正相关,可以从2个方面解释.首先,本实验开展时正值旱季,土壤前期含水量较低,不足以影响入渗过程;另一方面,套种、覆盖等措施同时具有较好的保水能力和改善土壤结构的功能,因而既表现出相对较高的土壤含水量,也表现出较强的水分入渗能力.另外初渗速率与土壤有机质含量正相关,表明土壤中有机质含量越高越利于土壤入渗.进一步探讨入渗速率与团聚体结构指标之间的关系,发现入渗速率与WSA0.25显著正相关,与 PAD0.25显著负相关,平均入渗速率还与MWD呈正相关关系(R2=0.62),说明土壤中水稳性团聚体含量越高,越有利于水分的入渗,团聚体高分散度则不利于土壤的水分入渗.土壤入渗速率与土壤理化性质之间的关系体现了不同的耕作措施会进一步改善土壤理化性质,如提高土壤团聚体稳定性的作用机制[30]、改变土壤有机质含量、降低容重等,从而增加土壤的入渗能力[31].

表4 土壤入渗速率与理化性质相关系数表Tab.4 Correlation coefficients between soil infiltration rate and influencing factors
2.3 不同耕作措施土壤入渗过程以及模型拟合 由5种耕作措施双环入渗实验的过程曲线(图1)看出,不同处理的入渗曲线在试验前10 min内呈现明显下降趋势,随实验时间的延长逐渐达到稳定入渗状态.顺坡和轮作的入渗曲线下降速率最快,且2种措施入渗曲线十分接近,在大约40 min时达到稳定入渗状态,整个入渗过程都低于其他措施,说明这2种措施的土壤不利于水分入渗.相比之下,套种的入渗曲线下降速率较慢且明显高于其他措施,达到稳定入渗的时间在50 min左右,这与前文所述套作具有较高的有机质和水稳性团聚体含量有关,说明套作利于改善土壤性质及其结构,增加土壤入渗能力.有机肥和覆盖措施的入渗曲线处在中间位置,其中覆盖的入渗曲线在入渗初期较高,但入渗速率随时间递减较快,其稳定入渗速率与轮作接近,说明如果不考虑地表秸秆拦蓄径流的作用,覆盖在降雨初期具有一定的减流效益,但对于长时间的持续性降雨减流能力有限.

图1 不同处理的入渗曲线对比Fig.1 Infiltration rates for the different tillage practices
使用Philip、Horton和Kostiakov入渗方程对不同耕作措施的入渗速率和入渗时间进行拟合,拟合参数和结果见表5和图2.
用Philip入渗方程拟合的吸渗率s值变化范围在21.57到26.55之间,s值越大入渗速率越大[32-33],由模拟结果可知,套作、覆盖和有机肥措施的s值最大且明显大于轮作和顺坡.由图2的1∶1线图可以看出,Philip公式对各措施稳定入渗速率(最低的5个数值)的估算值与实测值相比均显著偏高(ANOVA,P<0.001).整体上来看Philip公式对入渗速率的估算值与1∶1线较为接近,尽管对于最大入渗速率的估算存在一定程度低估,但对于各措施初始入渗速率(最高的5个数值)的估算值与实测值差异不大(ANOVA,P>0.05).
Horton入渗方程拟合的5种耕作措施的k值变化范围在0.04到0.08之间,各措施k值与入渗速率之间的关系并不明显.由1∶1线图可以看出,Horton方程对首个入渗速率普遍存在低估,特别是套作措施,其前5个初始入渗速率的估算值显著低于实测值(ANOVA,P=0.02).随着入渗继续进行,Horton方程的估算值开始超过实测值,除顺坡外各措施的估算值都在1∶1线以上.而到稳定入渗阶段估算值则又回到1∶1线附近,后5个稳定入渗速率的估算值与实测值差异不大.
由Kostiakov方程模拟的结果来看,不同耕作措施a值大小排序为:套作 >有机肥 >覆盖 >顺坡>轮作,这与实测的入渗曲线趋势一致,由模型拟合得到b值变化范围在0.34~0.53,覆盖的b值为0.53,说明其入渗速率衰减较快,这与图1覆盖措施实测入渗速率降低较快的现象吻合.Kostiakov方程的估算结果全程与1∶1线较为接近,估算得到的初始入渗速率和稳定入渗速率均与实测值差异不大.
进一步比较Philip、Horton和Kostiakov 3种入渗方程用于估算不同耕作措施入渗速率的模型有效系数均值,分别为0.73、0.88和0.95,由此可见Kostiakov模型更适于拟合本研究5种耕作措施土壤水分的入渗过程.
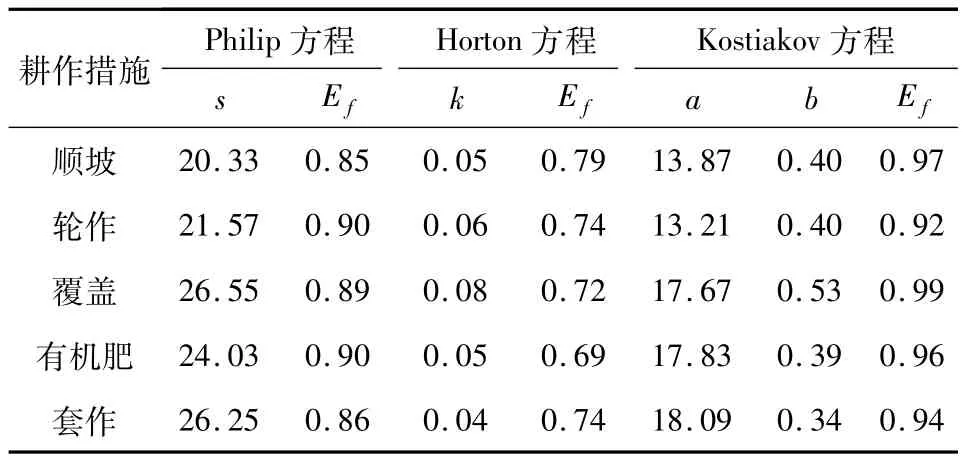
表5 不同耕作措施3种常见入渗方程的拟合参数Tab.5 Fitting parameters of infiltration of different tillage treatments

图2 3种模型对不同耕作措施入渗速率的拟合效果对比Fig.2 Comparison of the fitting effects of three models on infiltration rate of different tillage practices
3 研究结论
本文通过野外采样、模拟试验和数理分析,对比了典型红壤坡耕地5种耕作措施条件下的土壤性质和入渗能力,得出主要结论如下.
1)在红壤坡耕地采用套作、覆盖和有机肥处理的耕作措施可以显著增加土壤有机质含量,增强团聚体稳定性并改善土壤结构,从而提高土壤入渗能力.
2)从整体统计、过程分析和数理模拟的结果都可以看出,套作、覆盖和有机肥处理的土壤入渗能力指标均显著高于轮作和传统顺坡耕作措施,可见采用套作措施的土壤入渗能力最强,涵养水分的效益最优;入渗速率指标与土壤有机质含量、团聚体平均重量直径、水稳性团聚体含量呈正相关,与土壤容重、团聚体分散度指标呈负相关关系.
3)使用Philip、Horton和Kostiakov 3种入渗方程估算各耕作措施的土壤入渗过程,发现Philip将导致稳定入渗速率高估,Horton方程则可能低估初始入渗速率,而在后续阶段则存在高估问题,Kostiakov方程在入渗全程的拟合效果均较好,整体模型有效系数也表明该方程的估算精度较高,可用于估算本研究红壤坡耕地的土壤入渗过程.

