多视角思考 发散性思维——对一道模考题的多视角探求与思考

吴红霞

(江苏省南京市第九中学,210018)

数学知识的内部是有机联系、纵横交错的,很多问题,解题视角广、方法多,即使求解合理正确,未必就是最佳思路.因此,平时在解决问题成功时,不能就此罢手,更应深入探究,反思回顾,多视角、多层面探究和思考,寻求一题多解,冲破桎梏,揭示题目内部规律,拨开迷雾,加强对问题的领悟. 本文以一道高三模考填空题为例进行分析,以求冲破思维的禁锢,培养发散性思维能力,提升分析问题、解决问题的能力.

一、原题呈现

二、解法探究

视角1解三角形视角

解法1(利用正弦定理和余弦定理)

在∆ABP和∆BCP中分别使用正弦定理，得

①

②

③

在∆APC中,由余弦定理，得 22=PA2+PC2-2PA·PC·cos 135° .

④

分析2由于AB=BC,则S∆ABP=S∆BCP,从而由等面积法得到PA和PC的关系,再结合∆APC中余弦定理利用方程思想求出PA和PC.

解法2(利用等面积法和余弦定理)

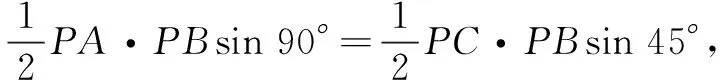
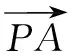
解法3(设角变量利用正弦定理和同角三角函数关系)

故PB=sinθ=cosθ-sinθ,

即 2sinθ=cosθ.

又sin2θ+cos2θ=1,θ∈(0,π),

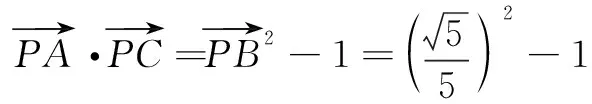
评注视角1的三种解法源于对数量积运算的不同转化,分别借助多次使用正、余弦定理解三角形,联立方程组得解,需要理顺图形中的各种边角关系,属于常规思路,也是学生的常用方法.

视角2平面几何视角

分析4在图2中,过点C作CD∥PA，与PB的延长线交于点D, 结合题中已知条件，可得等腰直角三角形PDC,进而解直角三角形即可.

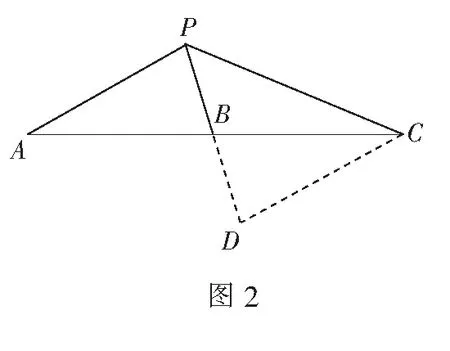
解法4(利用勾股定理)

如图2,过点C作CD∥PA与PB的延长线交于点D, 即PA∥CD,从而∠APB=∠PDC=90°,又AB=BC,则PB=BD,PA=CD.

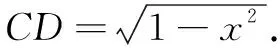
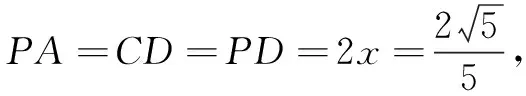
分析5在图3中,过点C作CE∥PB与AP的延长线交于点E.结合题中已知条件可得等腰直角三角形PEC, 进而解直角三角形即可.

解法5(利用勾股定理)

如图3,过点C作PB平行线与AP的延长线交于点E,即PB∥EC,从而∠APB=∠AEC=90°.

又AB=BC,则AP=PE,EC=2PB.

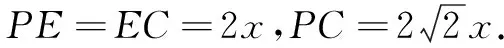
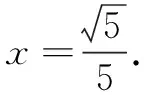
解法6如图4,过点A作PC的平行线与PB的延长线相交于点H,即PC∥AH,由AB=BC,得

PB=BH,AH=PC,

评注利用题中已知直角通过作平行线构造直角三角形是本方法的关键,利用勾股定理解直角三角形是根本.

视角3解析法视角

分析7坐标法也是解三角形和向量问题的常规方法,而且坐标法有思维量小的优势,几乎不需多想,只需找到解相关点坐标的条件即可,这是要让学生重视且要加强训练的方法.

解法7(利用坐标)

如图5,以点P为坐标原点,PA所在直线为x轴,PB为y轴建立平面直角坐标系,设A(a,0),B(0,b).

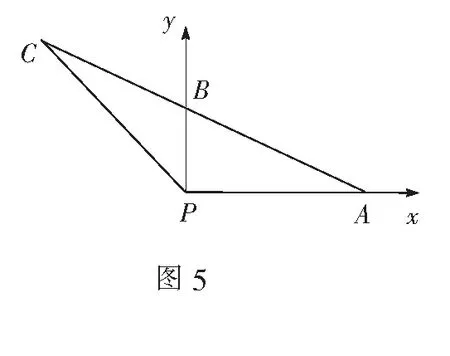
由题意知点B为AC中点,从而C(-a,2b).

又由∠BPC=45°得直线PC方程为

y=-x,则a=2b.

①

又AB=1,则a2+b2=1.

②

评注由题目条件中已知直角很容易联想到坐标法,建立坐标系时可以根据需要调整图形方向. 坐标法的优势是思维量小,化图形问题为坐标计算,方法的关键是找到解相关点坐标的条件.

三、解题反思

这是一道可以有效训练学生思维的好题,通过这一道题目,可以复习正、余弦定理，平面向量等多个知识点,加深巩固解三角形、几何法、坐标法等多种基本思想方法,同时也加强了向量运算、几何运算、坐标运算等相关运算能力,能根据题目的特点选择对应的运算途径也是要形成的能力之一.当然,运算能力离不开思维能力,有什么样的思维就有什么样的运算,多思考就少运算,少思考就多运算.

著名数学家、教育学家G·波利亚在《怎样解题》一书中指出:“好题目和某种蘑菇有点相似:它们都是成串成长,找到一个以后,我们应该看看,很有可能在很近的地方又能找到更多的.”因而当解完一道题以后,要不断领悟反思,多视角切入进行深度挖掘,从而达到一题多解、触类旁通的效果. 通过典型实例的一题多解,使得解题思路更加开阔,数学知识的掌握更加熟练牢固,同时也可以拓展思维,妙法顿生,提高解题速度,培养发散思维能力,激发学习的主动性、积极性和趣味性,全面提高知识水平和思维能力.