高观点下的代数证明方法探究

四川师范大学数学科学学院(610011) 王金隆 张 红 申 涛

1 研究背景

德国数学家菲利克斯. 克莱因在《高观点下的初等数学》中,提出“数学专业的大学生,学到的专业知识不少,但是许多重要的,以及在中学任教中用得着的部分往往被忽视了.《高观点下的初等数学》正着眼于弥补这些缺憾,揭示各部分之间的联系”[1]. 并且他认为教师应该具备较高的数学观点. 理由是,观点越高,事物就越显得简单. 例如,实数中不好理解的某些东西,在复数域的观点看,就比较清楚了.

高观点指的是,用高等数学的观点、方法、原理,解决中学的数学问题. 最近几年,将高观点和高考题结合在一起,成为近几年对高考分析的热点. 例如,2019年胡琳的《高观点下高考数学试题分析》[2]一文中,介绍了2017年全国二卷文科21 题应该如何处于高观点的视角下分析. 而高观点下的数学教学一直是中学研究的热点. 最早研究高观点的文章课追溯到1991年,庞征球发表在《淮北煤炭师范学院学报》上的《高观点下的初等数学教学探索》[3],在文章中给出了几个用高观点指导教学的例子. 而1991—2019年,一共有80 余篇有关高观点指导教学的文章.

近年来,将一个问题同时用初等数学和高等数学两种方法来解决,也成为了研究热点. 这一方面是由于越来越多的高考题、竞赛题,特别是自主招生题,都或多或少有着高等数学的背景,另一方面也是由于中小学老师对于高观点下的解题越来越重视,特别是高校教师的参与,使得初等数学和高等数学结合得更加紧密.

在中学用多种方法解答同一道数学题,其好处是明显的,不仅仅将许多知识点,以同一道数学题为载体串联起来,达到牢固掌握和运用所学知识点的目的. 更重要的是,通过多角度的思考,不同解法分析比较,可以找到解题的最佳途径和方法,培养创造性思维和能力. 也能体会高观点与初等思维之间的优劣性.

中学老师研究高等数学,还是要落脚在初等数学问题上.基于此,我们认为可以参考一些例题,分别用初等数学和高等数学的方法来解答,通过对比分析方法的特点,加深对初等数学和高等数学的理解. 而这些题目往往就是沟通高等数学和初等数学的桥梁.

2 实例研究

笔者通过文献查阅,代数证明的方法可以从大的方向分为以下两类,分别是初等代数方法,高等代数方法.

2.1 初等代数方法

笔者认为,初等代数方法,即是使用简单的运算以及利用公式的变形,或者是等式的性质等. 其中简单的运算包括:加、减、乘、除、开方、乘方等;公式包括:平方差公式,完全平方公式,立方差公式,立方和公式,等比、等差数列通项以及求和公式等. 等式的性质包括:等式两边同加、同减、同乘一个相同的数,等式成立. 等式两边同时除以一个非零的数,等式成立.

题目1求证:a2+b2= 1,c2+d2= 1 的充要条件是:a2+c2=1,b2+d2=1,ac+bd=0.

说明:由于已知条件和结论具有超强对称性,反向推导方法完全一样.

证法1若b= 0,则有a2= 1,c= 0,d2= 1,显然结论成立. 反之,当b0,则可设a=bk,d=−ck,代入条件可得:

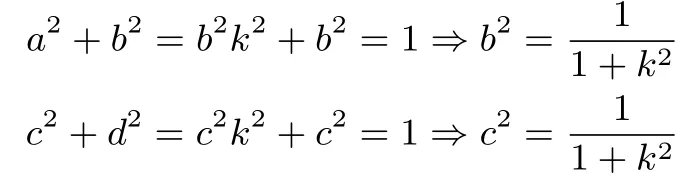
由此可得:b2=c2,则a2+c2= 1,b2+d2= 1,ac+bd=b2k −c2k=0,即得证充分性.

证法1 是首先给出特殊值证明成立,然后设一个待定系数,利用这个待定系数建立一个中间等量这里的k不需要求出具体数值,体现了初等代数解题“设而不求”的数学思想,从而得到b2=c2. 证法1 使用的只有初等代数的方法证明.

证法2因ac+bd=0,则有a2c2=b2d2,又a2+b2=1,则有a2c2+b2c2=c2,则有

故可得b2=c2, 若b=c, 因ac+bd= 0, 可得ac+bd=ab+cd=0,若b=−c,因ac+bd=0,可得ab+cd=0,即得证.

证法2 是利用等式的性质,首先等式两边减去bd,之后同时平方,等式仍然成立. 接着等式两边同时乘以c2,等式仍然成立. 证法2 使用的只有初等代数的方法证明.

证法3设a=sinA,b=cosA,c=cosB,d=sinB,因为ac+bd=0,则有

即sin(A+B)=0,则有A+B=kπ,k ∈Z,

即得证.

证法3 是从题目条件联想到三角代换, 思路清晰自然,联合三个条件给出这一关键信息,推导所要求的结论也就变得不是那么难. 证法3 利用换元法,将代数证明与三角函数联系在一起,使用的仍然是初等代数的证明方法.

证法1、证法2、证法3 都是使用的初等代数的方法. 其中证法1 利用中间量进行证明,这个中间量如何构造,构造在何处,都是这一证法的难点;证法2 利用等式的性质进行变形,怎么变形,往什么方向变形则是这一证法的难点. 证法3 利用三角代换证明,怎么联想到三角代换,和哪一个量进行代换,是这一证法的难点. 这些难点都不是一天两天能够熟练掌握的,而是需要学生日积月累的思考和强化. 对于相关的题型、变式、公式的变形等等,都需要多多理解,多多总结.

2.2 高等代数方法

笔者认为,高等代数思想方法,就是使用矩阵、行列式、线性空间、欧式空间等对初等代数的问题进行解答. 即不仅仅使用等式的性质这些,而是运用矩阵等方法对初等代数证明进行解答.

题目仍然选择之前证明的题目,这样更能体会高等代数方法与初等代数方法的联系与区别.

即求证:a2+b2= 1,c2+d2= 1 的充要条件是:a2+c2=1,b2+d2=1,ac+bd=0.

说明:由于已知条件和结论具有超强对称性,反向推导方法完全一样.

证法4将a2+b2=1,c2+d2=1,ac+bd=0 写成矩阵的形式,即

将a2+c2=1,b2+d2=1,ac+bd=0 写成矩阵的形式,即

证法4 就运用到了高等代数的方法,把条件和结论中的三个式子都放进了矩阵之中,最后再利用正交矩阵的性质将充分性和必要性一起解决. 这样就可以看出初等数学和高等数学之间的界限其实很不明显.

证法5有一恒等式:

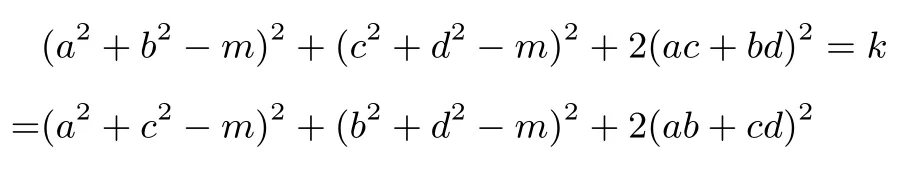
在此题中只是当m=1,k=0 的特殊情况,此恒等式和拉格朗日恒等式很像. 验证此恒等式的正确性,只需展开即可.

证法6有一意大利数学家斐波那契给出的恒等式:

则可得到

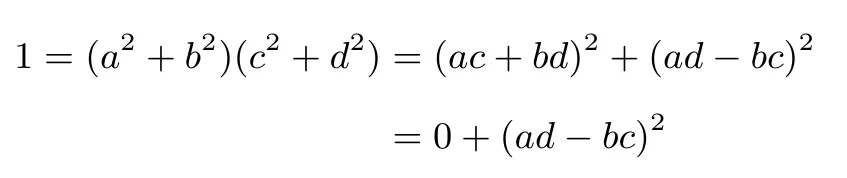
则可以得到ad−bc=±1,将ac+bd=0 代入a2d−abc=±a可得a2d+b2d=±a, 故a=±d, 同理可得b=±c, 则a2+c2=1,b2+d2=1,ac+bd=0,即得证.

证法5、证法6 都用到了恒等式,但是相对而言,证法6要更清楚,证法5 所涉及的恒等式对于学生来讲是比较难想到的,而证法6 很容易得到故a=±d,b=±c. 但是推广,计算求解时就不太容易,反而不如证法5 那样模模糊糊的证明.

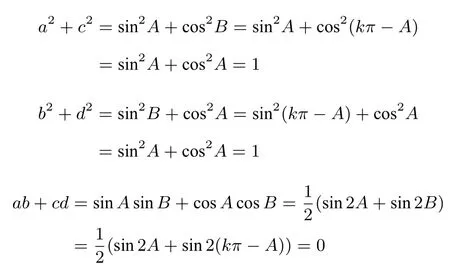
综合以上所有的证法,要讲清楚这道题,就需要考虑到学生的知识水平处于何种阶段. 高中生中等水平可能需要考虑前三种,而知识水平更高的就可以考虑证法4,因为证法4涉及到矩阵的一些知识,但是证法却是很简单的,也深刻体现出了高观点下解决中学数学问题的优越性.

3 研究启示

初等代数方法与高等代数的方法,在证明初等代数的题目中,两种方法各有优劣,对于优等生可以要求掌握高等代数方法,这样解题的时间就会缩短,并且学生的数学思维也能达到高瞻远瞩的效果. 并且在证明时也各有优劣,各有利弊,需要学生对其能够有一个整体的把握.

初等代数方法,理论简单,涵盖丰富,但是操作较为复杂.怎么去构造中间量,怎么去变形,怎么代换都是这类方法的难点所在. 要克服这些困难,需要学生对这类题目有一个整体的把握,和日积月累的练习.

高等代数方法,方法较为简单,但是理论比较困难,具有一般性. 首先学生得先了解矩阵、拉格朗日恒等式、斐波那契恒等式等高等代数知识是什么? 他们有何作用,使用这些知识应该注意哪些,则是高等代数方法的难点.

初等数学研究是一个大课题,高等数学研究也是一个大课题. 将两个结合起来研究,涵盖的更广,且绝对不是两者简单相加. 对于这两者结合的这么大的课题,绝对不是一个人、几个人发几篇文章能够研究清楚的. 需要的是大量的学者研究.

4 “代数证明”的教学设计

教学目标

1.1 知识与技能目标

掌握代数证明的两种思想方法; 对于某一代数证明题,使用两种或者三种方法进行解答;

1.2 过程与方法目标

以某一代数证明题为基础,引导学生从不同角度,不同方向,不同方法进行思考,从而加深学生对于不同方法的理解,体会高观点下的方法与初等方法之间的联系与区别.

1.3 情感与态度目标

从学习代数证明出发,让学生体会高观点之下的初等数学,从而体会知识用浅人深的过程,激发学生自身的学习兴趣,并且能够锻炼学生遇到问题的应变能力,培养学生的理性思维.

教学重点、难点

2.1 重点找到高等代数思想方法与初等思想方法的联系与区别;

2.2 难点代数证明的两种解题方法;

教学方法和手段

基于本次课的教学内容以及教学重难点,以学生的知识基础为起点,在教学中运用教师讲授、小组讨论、教师总结的三种方法,为学生营造很好的学习氛围.

教学过程

环节一例题1 的讲解,运用初等代数方法证明

问题1、平方差公式的形式是什么样子的?

问题2、因式分解时我们应当注意哪些?

问题3、方程解的结构是什么样的?

设计意图本环节旨在考验学生的基础,对学生已有的知识基础有个整体的把握. 题目中的解法包含了平方差公式、因式分解,所以应当对这部分的知识进行复习. 而留下一个方程解的结构,引发学生的思考.

涉及知识点

1. 平方差公式

2. 因式分解

题目:把多项式x4+x3+x2+x+1 表为两个次数不同的实多项式的平方差,并证明只有四组解.

证法1因为要将x4+x3+x2+x+1 表示为两个多项式的平方差,故设:

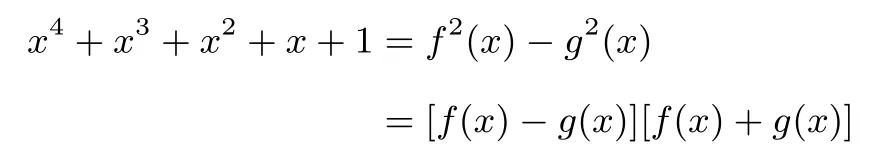
又因为x4+x3+x2+x+1 的系数都是1,故将其因式分解.

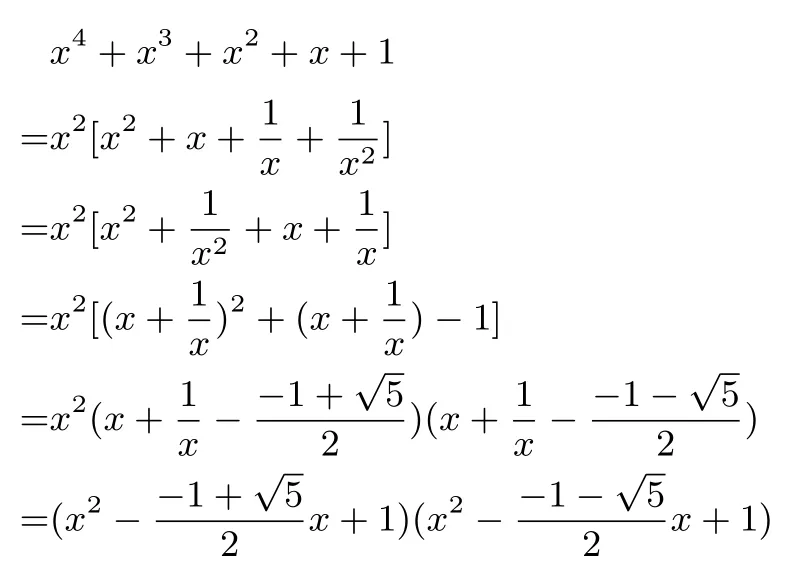
则可将f(x),g(x) 看成两个未知数, 故可以通过解二元一次方程组将其解出来. 即并且, 由题知, 若 (f(x),g(x)) 是一组解, 那么(f(x),−g(x))(−f(x),g(x))(−f(x),−g(x)) 也是解, 则共有四组解.

分析:这种方法都是初等代数方法,利用等式的性质,公式法,以及因式分解. 这些思想的难点都是方向性问题,怎么变换是难点. 对于学生来说,寻找这些思想的方向较难,故造成了初等代数方法过程简单,但是思维很难.

环节二这一题的分析是初等代数的方法,那是否还有其他的方法呢?

1、对多项式的次数有什么认识?

2、是否接触过首一多项式?

设计意图之前经历了初等代数的方法,学生没有新鲜感,就会没有那么大的学习兴趣. 这时候提出几个学生没有听过的名词,从而引起学生的好奇心,激发学生对这些知识的学习兴趣.

涉及的知识点

1、首一多项式

2、多项式次数

题目把多项式x4+x3+x2+x+1 表为两个次数不同的实多项式的平方差,并证明只有四组解.

方法2:因为要将x4+x3+x2+x+1 表示为两个多项式的平方差,故设:

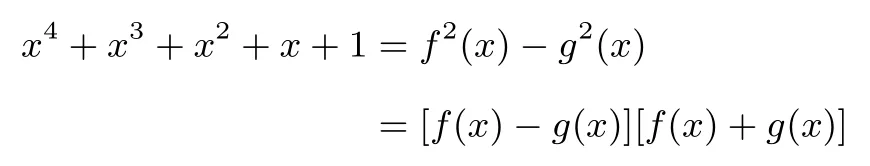
又因为是两个次数不同的多项式,故deg(f(x))=deg(g(x)),则deg2(f(x))=deg2(g(x)).

又假设deg(f(x))deg(g(x)).

总结:对比高等与初等代数证明的方法,可以看出初等方法中怎么对公式变换较为困难,并且解法较为特殊,并不具有推广性. 而高等代数的方法更严谨,并且方法具有可推广性,如果学生储备这些知识,对于这些证明题就会感到很容易.

环节三教学反思

(1)精心备好一节课,是上好一节课的基础. 如果教师在备课中没有更高的视角,没有高观点的基础,那么课堂将没有深层次的研究,对学生求异思维的培养将是空谈.

(2)注重学生的差异性,不同层次的学生所想到和掌握的方法一定是不同的,问题的解决不是指答案的得到,而应指向方法的提炼与思维的形成. 所以在问题解决的过程中,才需要寻求解决策略的多样性,这样可以满足各个层次学生的学习需求,也能更好地.

(3)例题的价值是由例题所包含的思维含量决定的,教师的作用在于对题目思维含量认识到位后构建有效的教学形式. 在平时的教学中,可能因为时间、精力、教学习惯等原因就例题而讲例题, 长此以往不仅教师教学水平徘徊不前,更重要的是学生能力得不到培养. 作为一线教师,要深入研究例题的基础上,对例题进行合理地教学设计,从而通过有效教学手段引导学生抓住为题的本质,让学生学到知识,学到方法,学会思考.

综上所述,借助高观点来培养学生,依照研究的对象所提供的信息,沿着不同的方向去思考,对信息和条件加以重新组合,探求多种解决方案或新途径的思维形式是我们教师任重道远的任务. 也是一个值得我们探讨和努力地研究课题.