一类极限结论若干证明方法与应用
王成强
(成都师范学院 数学学院, 四川 成都 611130)
0 引言
大学数学中的很多知识模块是从极限知识模块展开的[1-3],例如,Taylor展开式理论是建立在可微函数类上的,而函数可微性的定义直接依赖于函数的极限理论;又如,函数的Riemann积分就是该函数在给定的区间分割上的Riemann和的极限。极限理论是Taylor展开式理论与Riemann积分理论的基础,而Taylor展开式理论与Riemann积分理论反过来又为处理某些极限问题带来极大的便利[4-5]。本文旨在针对一类极限结论,设计若干基于Taylor展开式理论与Riemann积分理论的证明方法,以期为大学数学中的极限、Taylor展开式与Riemann积分的教与学带来更多思考。本文要证明的极限结论完整表述如下。
结论(*)[6]设函数f(x)在有限闭区间[a,b]上二次可微,且二阶导数f″(x)在区间[a,b]上的Riemann积分存在。证明


在本文给出的结论(*)的几种证明方法中,函数Riemann积分的定义本身有重要应用,与之等价的Riemann可积条件也有重要应用:对任何ε>0,都存在δ>0,使得对区间[a,b]的任何分割a=x0 就有 本文用到的主要工具有一元函数与二元函数的带Lagrange型余项的Taylor展开式。一元函数的Taylor展开式完整表述如下:若h(x)在区间(x0-r,x0+r)上n+1次可微,则对任何x∈(x0-r,x0+r),都存在严格介于x0与x之间的实数ξ,使得 主要用到的二元函数的Taylor展开式完整表述如下:若u(x,y)及其偏导数ux、uy、uxx、uxy、uyx、uyy都在区域(x0-r1,x0+r1)×(y0-r2,y0+r2)上连续,则对区域中的任何点(x,y),都存在θ∈(0,1),使得 本文将基于不同视角,综合利用函数Riemann积分的定义、一元函数与二元函数的带Lagrange型余项的Taylor展式,给出结论(*)的4种证明方法,并利用结论(*)中的公式给出数列极限题的简洁解答的一个例子。 使得 使得 或等价地,使得 于是 仿照证法1,可完成证法2的其余步骤。 使得 接着仿照证法1与证法2即可完成证法3的其余步骤。 基于此,进一步还可得:对任何k=1,2,…,n,都存在 使得 对∀ε>0,因为函数f″(x)在区间[a,b]上Riemann可积,是故存在N>0,使得对任何n>N,都有 借助于这些分析,并经过一些常规但繁琐的计算,有 由数列极限的ε-N定义,结论(*)得证。 在结论的证法1中,用了两次变限积分形式的一元函数的Taylor展开式;在证法2中,只用了一次变限积分形式的一元函数的Taylor展开式;在证法3中,用了一次变限积分形式的二元函数的Taylor展开式;在证法4中,用到的是结论(*)给定函数的Taylor展开式与Riemann可积的充分必要条件,而并未用到变限积分形式函数的Taylor展开式。相较而言,证法4的想法最直接但步骤最复杂,证法2的解答步骤最简洁,但用以施加Taylor展开式的函数的选取最精妙。 例1[6]计算数列极限 借助于1.1小节证法1~4中的想法,再仿照它们的证明过程,可给出例1中的数列极限的4种计算方法,但从证法1~4的证明过程中可察觉,其过程极其复杂。经分析后发现,直接利用结论(*)可给出例1一种简洁的解答。 解直接运用结论(*)中的公式,有 或等价地,使得 在此基础上,经过一些常规运算就能证得

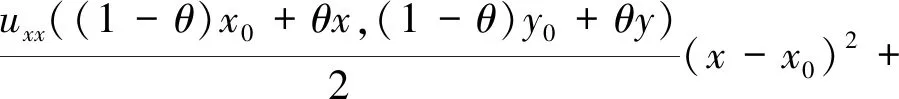
1 结论(*)的4种证法与应用
1.1 结论(*)的4种证法

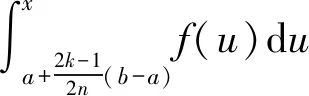
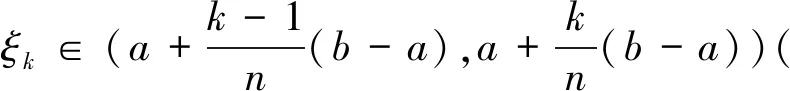

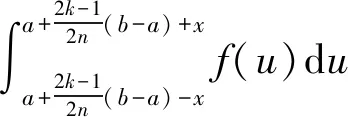
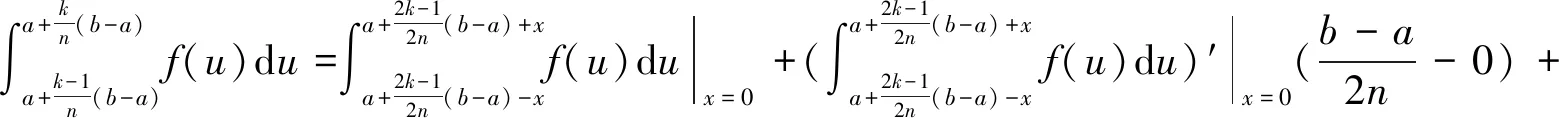
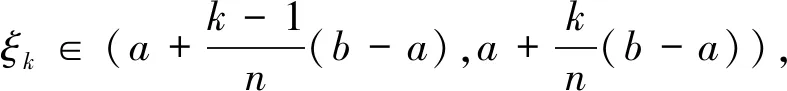

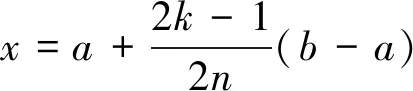
1.2 应用举例

2 结束语