任意旋转角三维坐标转换的微分罗德里格矩阵算法

罗翔，刘志平

(1.中国矿业大学 江苏省资源环境信息工程重点实验室，江苏 徐州 221116;2.中国矿业大学 环境与测绘学院，江苏 徐州 221116)

0 引 言

三维坐标转换是空间大地测量应用中坐标成果换算的基础工作，其常用模型包括Bursa-Wolf模型、Molodensky模型和武测模型。很多学者对上述七参数模型进行，研究和改进，如针对线性化系数矩阵病态问题的重心化方法[1]；解决参数相关性的两步解法[2]；考虑参数先验信息的序贯平差法[3]等。这些算法在一定程度上提高了模型适用性，但均将坐标旋转角视为微小值，仅适用于小旋转角的坐标转换[4-7]。为解决任意旋转角坐标转换问题，国内外学者提出多种三维坐标转换方法：文献[8-10]基于四元数理论[11-12]将旋转矩阵用单位四元数表示，通过四元数的迭代更新获得旋转参数，适用于任意旋转角，然而迭代存在繁琐的矩阵求导过程；文献[13-15]利用9个方向余弦参数表示旋转矩阵，虽适用于任意旋转角，但模型参数达到13个，迭代收敛慢；基于罗德里格矩阵理论，文献[16]采用非迭代解法，忽略了随机模型对参数估计的影响；文献[17-19]采用参数偏导数求解雅可比矩阵，形式复杂且收敛性差。本文针对上述空间坐标转换参数求解中矩阵求导复杂、迭代收敛慢、随机模型不严密等问题，利用罗德里格矩阵、反对称矩阵与向量积运算性质，通过罗德里格矩阵微分与参数微分变换导出任意旋转角三维坐标转换函数模型、随机模型同步收敛的新方法，简称微分罗德里格矩阵算法。最后通过文献算例和模拟算例将此方法与四元数、方向余弦、罗德里格矩阵算法进行坐标转换对比研究，以评估该算法正确性及实用性。

1 三维坐标转换模型

1.1 基于罗德里格矩阵的转换模型

设xi和Xi分别为空间一点在A,B空间直角坐标系中的坐标，则他们存在如式(1)的转换关系：

xi=k·R·Xi+T-εi，Dε,

(1)

目前，任意角旋转矩阵R可由旋转角余弦、罗德里格矩阵、单位四元数等方式构建。本文采用罗德里格矩阵表示的三维坐标转换模型，其任意角旋转矩阵R表示形式为

(2)

1.2 微分罗德里格矩阵解法

将式(2)代入式(1)，即可得基于罗德里格矩阵的三维坐标转换模型，若按矩阵求导方式对该模型进行参数线性化展开，其步骤繁琐不易实现。下文利用罗德里格矩阵和反对阵矩阵的性质构造微分罗德里格矩阵算法，避免了复杂矩阵求导计算和化简，推导过程如下。

由式(2)可以推导出罗德里格矩阵R和反对称矩阵S满足如下性质，

(3)

将式(2)代入式(1)可得

式(4)两端乘(I3-S)，可得

(I3-S)xi+(I3-S)εi=

k(I3+S)Xi+(I3-S)T，

(5)

将反对称矩阵S，尺度参数k和平移向量T用初值项和微分项之和表示，即令S=S0+Sd，T=T0+dT，k=k0+dk，代入式(5)进行整理化简，并保留至微分项一阶项，可得

(I3-S0)xi-k0(I3+S0)Xi-(I3-S0)T0+

(I3-S)εi=dk·(I3+S0)Xi-

Sxi+k0Xi-T0·d+(I3-S0)·dT,

(6)

式中，反对称矩阵与向量积运算性质满足Sd·(*)=-S*·dα，*表示任意列向量。

进一步，式(6)两端乘(I3-Sα0)-1进行还原，并结合式(3)化简，可得

(7)

(8)

利用最小二乘法，可得模型参数改正数的迭代估计式，即

(9)

通过式(9)迭代更新参数估值，继而更新系数矩阵A和观测值L，迭代计算直至满足迭代停止条件。分析上述推导过程可知，该方法充分利用了罗德里格矩阵、反对称矩阵以及向量积运算的性质，将罗德里格矩阵微分转换为参数向量微分形式，避免了三维坐标转换模型中的矩阵求导，实现了三维坐标转换函数模型和随机模型同步迭代逼近的微分罗德里格矩阵解法。

1.3 模型参数初值估计

(10)

根据式(1)将重心化坐标模型表示为

基于式(11)，利用反对称矩阵与向量积运算性质S·(*)=-S*·α，可以导出反对称矩阵参数初值的估值

(12)

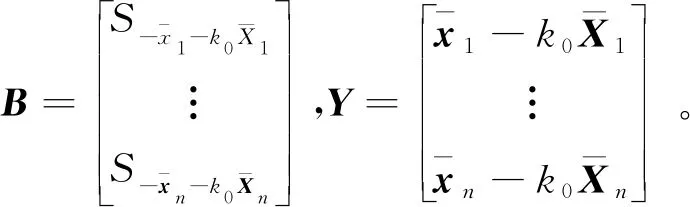
进一步，平移参数初值可按式(13)计算

(13)

2 计算结果与分析

2.1 现有文献算例

为验证本文所提的微分罗德里格矩阵算法的正确性和有效性，利用该方法对现有文献算例进行实验分析。使用文献[7]的数据，选取9对控制点进行实验。控制点转换前后坐标系分别为WGS84坐标系和西安80坐标系，覆盖范围较大，但两组坐标旋转角度相对较小。

表1 文献算例转换坐标及其较差

表1中ΔX,ΔY,ΔZ为通过转换参数求得的转换坐标与原始坐标的较差。由表1可见，利用本文提出的微分罗德里格矩阵算法反算出来的坐标，点位较差最大为36.201 mm，与文献[7]中所计算36.2mm的最大点位较差一致。说明本文方法能够准确地求出小旋转角的转换参数，验证了算法正确性和小旋转角有效性。

2.2 模拟实验算例

为更全面地验证所提算法的正确性和大旋转角有效性，选取经度117.0°～117.8°，纬度33.0°～33.8°，以0.1°为步长形成9×9=81个格网点坐标作为源坐标，令大地高均为0，利用CGCS2000椭球参数计算各点空间直角坐标，再将格网点坐标基于模型式(1)按模拟转换参数计算目标坐标。模拟参数取值方案为3个旋转角取值范围为[-90，90][-180，180][-180，180]，以15°为步长得到13×25×25=8 125组；平移参数固定为(x，y，z)=(1.0，1.5，2.0)×103；尺度参数固定为k=(1+10-5)。考虑到实际中存在的观测误差，在经过上述参数理论值转换后的坐标三维分量中加入0.005 m的随机误差。

将本文微分罗氏矩阵与单位四元数法[8]、方向余弦法[14]、常规罗德里格矩阵[19]进行参数求解试验对比，每组试验数据重复100次，迭代准则不变，统计每组试验数据迭代次数、单位权中误差、参数真误差等指标评判方法的正确性和有效性。计算结果如表2所示。

表2 模拟算例计算结果统计

由表2知，4种算法均获得了正确的解算参数，其中：尺度参数误差均值量级在10-8量级；旋转角参数误差均值在10-3秒量级；平移参数误差在10-1m量级，验证了4种算法正确性和大旋转角适用性。进一步综合比较迭代次数、单位权中误差和参数精度指标，可以得出本文算法有以下特点。

(1)更少的迭代次数。从迭代次数统计看，本文所提算法的迭代次数均值在5次以下，明显优于方向余弦算法(20次)、四元数算法(14次)和线性罗氏矩阵(19次)，且迭代次数中误差小，说明该算法迭代稳定、收敛速度快。

(2)更小的单位权中误差。从单位权中误差统计看，3种算法计算结果基本一致，均在给定的误差水平(5 mm)，但从其统计量中误差可看出，本文算法中误差最小，表明本文算法比其他两种方法更具有统计优势。

(3)更高的参数准确性。从求解参数的真误差统计可以看出：4种算法尺度参数真误差几乎完全一致；角度和平移参数真误差中，本文算法误差最大值、均值、中误差均小于其他3种算法，这表明本文算法求解参数的准确性优于其他3种算法。

为了进一步直观表达新算法的优点，统计迭代次数和参数真误差的频数直方图，结果如图 1所示。由图1可看出，本文算法、方向余弦算法、四元数算法、常规罗氏矩阵迭代次数分别集中(累计60%以上)在10次以下、10～30次、10～20次、10～30次；尺度参数真误差几乎完全一致；角度参数真误差分别集中在0～2×10-3″，0～4×10-3″，0～4×10-3″，0～4×10-3″间；平移参数真误差分别集中在0～2，0～3，0～3，0～3 dm间。综上，迭代次数和参数真误差中，本文算法均优于其他3种算法，表明其收敛速度快、参数准确性高，与前文的分析结论一致。

图1 迭代次数和参数真误差统计

3 结 论

本文从常规任意旋转角空间坐标转换模型线性化复杂、迭代收敛速度慢、精度低等问题出发，利用罗德里格矩阵和反对称矩阵的微分形式推导出一种适用于任意旋转角的空间坐标转换参数快速迭代求解算法——微分罗德里格矩阵算法。通过现有文献算例和模拟算例分析，基于迭代次数、中误差、参数真误差等指标，得出了以下结论：

(1)本文提出的微分罗德里格矩阵算法适用于任意旋转角的三维坐标转换。

(2)通过大量模拟数据验证，相较于经典四元数算法、方向余弦算法、常规罗德里格矩阵算法，本文算法在收敛速度、参数精度上具有显著优势。