滞后型泛函微分方程的解关于初值的可微性

李宝麟， 杨银杏

（西北师范大学数学与统计学院，甘肃兰州730070）

Kurzweil于1957年建立的广义常微分方程理论［1］在处理常微分方程、脉冲微分方程、滞后型泛函微分方程及拓扑动力系统等问题时有着重要作用，且被许多学者进行深入广泛的研究，取得了一些新的成果［2-5］.

在经典常微分方程理论中，方程

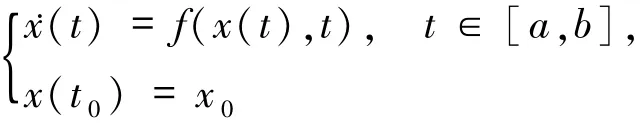
的解关于初值条件可微是指在一定条件下，如果方程右端函数f关于x可微，那么函数是可微的，其中x（t，x0）表示方程的解在t∈［a，b］处的值.Federson等［6］建立了滞后型泛函微分方程与广义常微分方程的等价关系，从而广义常微分方程中的很多相关理论都可以应用到滞后型泛函微分方程中.文献［7］研究了广义常微分方程的解关于初值和参数的可微性，主要工作如下：尽管广义常微分方程的解关于t不一定是可微的甚至不是连续的，但方程右端函数关于x（或关于参数）的可微性仍能保证广义常微分方程的解关于初值条件（或参数）是可微的.本文借助滞后型泛函微分方程与广义常微分方程的等价关系，考虑滞后型泛函微分方程

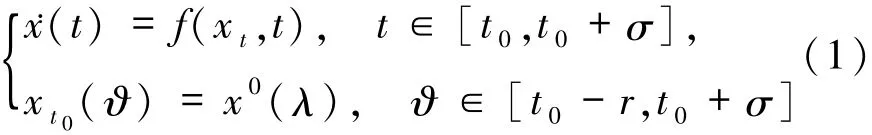
的解关于初值的可微性.

记G（［a，b］，Rn）是正则函数x：［a，b］→Rn构成的空间，即对紧区间［a，b］，单侧极限

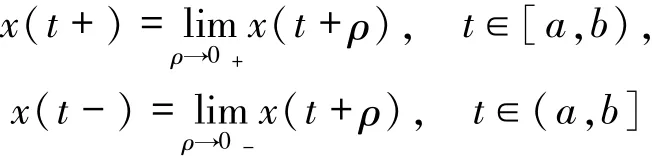
分别存在且有限.区间［a，b］⊂R，对所有的

定义

则G（［a，b］，Rn）为Banach空间.给定函数

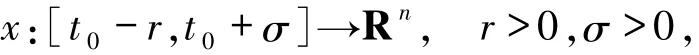
考虑

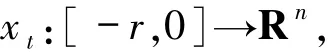
由

给定，则对函数

有

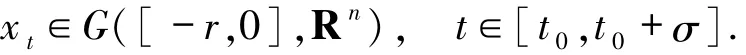
设开集

且具有下列性质：如果

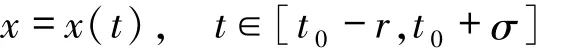
给定且属于G1.特别地，G（［t0-r，t0+σ］，Rn）中的任意开球都具有此性质.

方程（1）等价于积分方程

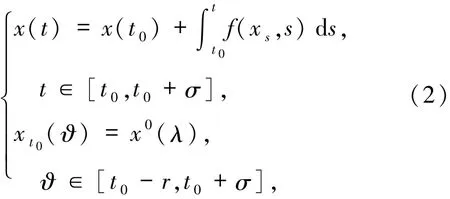
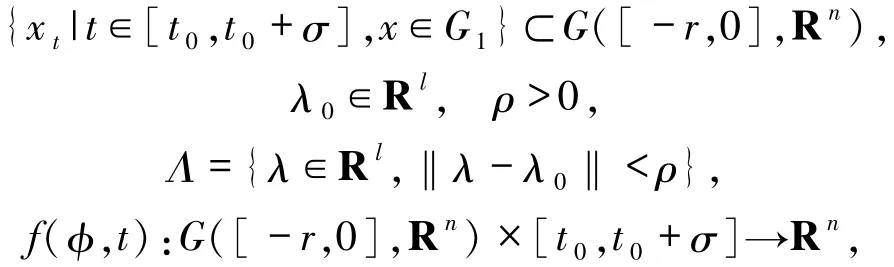
（A）对所有的x∈G1，u1，u2∈［t0，t0+σ］，存在Lebesgue可积函数M：［t0，t0+σ］→R，使得

（B）对所有的x，y∈G1，u1，u2∈［t0，t0+σ］，存在Lebesgue可积函数L：［t0，t0+σ］→R，使得

本文利用广义常微分方程的解关于初值的可微性，讨论滞后型泛函微分方程（1）的解关于初值的可微性.

1 预备知识

下面介绍本文要用到的广义常微分方程与滞后型泛函微分方程的概念与结论.

定义1.1［8］设函数

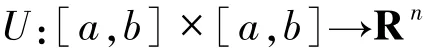
在区间［a，b］上称为Kurzweil可积的，如果存在I∈Rn，使得对任意的ε＞0，存在正值函数

对［a，b］的任何δ-精细分划

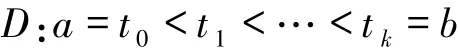
及｛τ1，τ2，…，τk｝，有

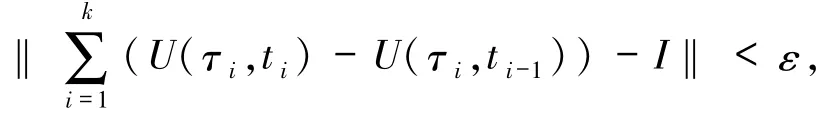
其中

则I∈Rn称为U在区间［a，b］上的Kurzweil积分，记作

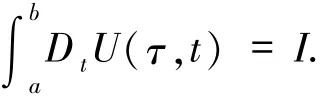
特别地，当

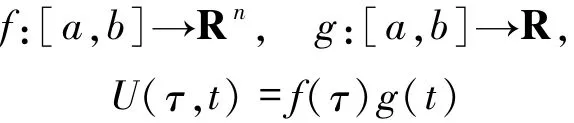
时，上面定义的积分称为K-S（Kurzweil-Stieltjes）积分，记作

定义1.2［7］设F：Ω→Rn，Ω⊂Rn+1，函数

若对所有的

有

其中右端积分为Kurzweil积分，则称x为广义常微分方程

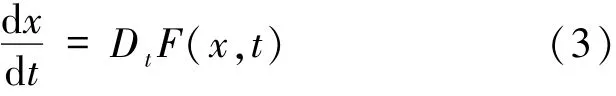
的解.

定义1.3［8］设函数F：Ω→Rn，其中

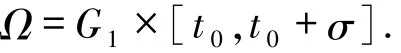
如果F属于函数族F（Ω，h，ω），则下列条件成立：对任意的（x，t1），（x，t2）∈Ω，有

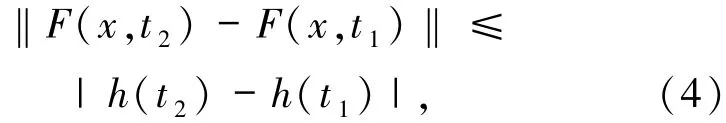
对任意的（x，t1），（x，t2），（y，t1），（y，t2）∈Ω，有

其中h：［t0，t0+σ］→R为不减连续函数，ω：［0，+∞）→R是连续的增函数且ω（0）＝0.

引理1.1［7］若f：［a，b］→Rn为正则函数，g：［a，b］→R为不减函数，则积分（K-S）

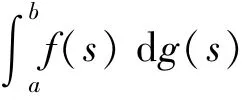
存在.

注1如果f关于g是L-S（Lebesgue-Stieltjes）可积的，则f关于g是K-S可积的（见文献［8-9］）.

引理1.2［7］设f：［a，b］→Rn为正则函数，g：［a，b］→R为不减函数，U：［a，b］×［a，b］→Rn×n是Kurzweil可积的，若对任意的τ，t，s∈［a，b］，有

‖U（τ，t）-U（τ，s）‖≤f（τ）｜g（t）-g（s）｜，则

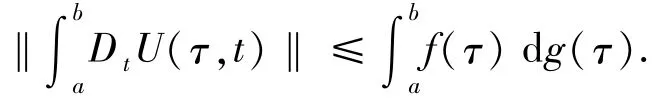
引理1.3［7］设函数U：［a，b］×［a，b］→Rn×m是Kurzweil可积的，u：［a，b］→Rn×m是U的原函数，即如果U关于第二个变元是正则的，那么u也是正则的，且满足

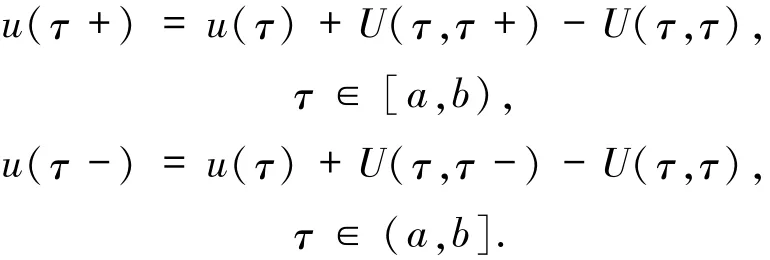
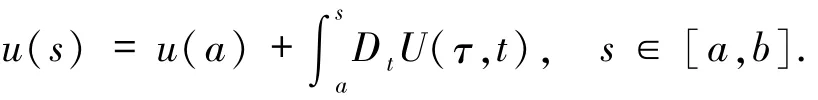
更进一步，若存在不减函数h：［a，b］→R，使得

则

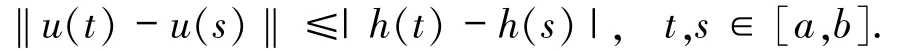
引理1.4［7］设函数

且A满足

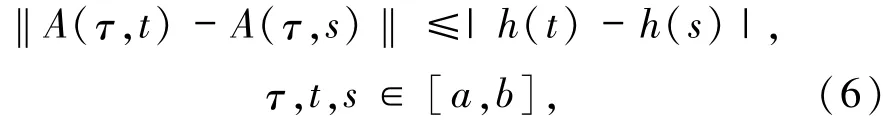
其中h：［a，b］→R为不减左连续函数.若对任意的s∈［a，b］，有

则z在区间［a，b］上是正则的.

引理1.5［7］设函数A：［a，b］×［a，b］→Rn×n是Kurzweil可积的，且A相对于左连续函数h满足（6）式，则对于每个z0∈Rn，初值问题

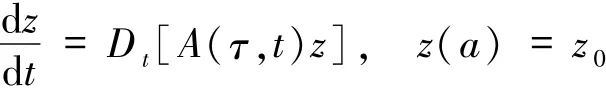
存在唯一解z：［a，b］→Rn.

引理1.6［8］设h：［a，b］→［0，+∞）是不减左连续函数，k＞0，l≥0.设ψ：［a，b］→［0，+∞）有界且满足则对任意的ξ∈［a，b］，有

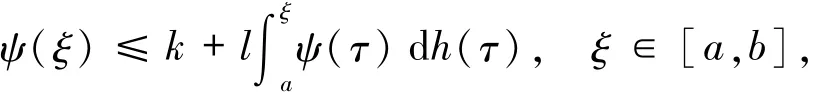
引理1.7［6］f（φ，t）：G（［-r，0］，Rn）×［t0，t0+σ］→Rn满足条件（A）和（B）.

（i）设y（t）是滞后型泛函微分方程

的一个解.给定t∈［t0-r，t0+σ］，令

则

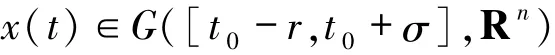
是广义常微分方程

的一个解，其中

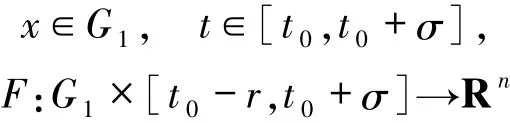
且

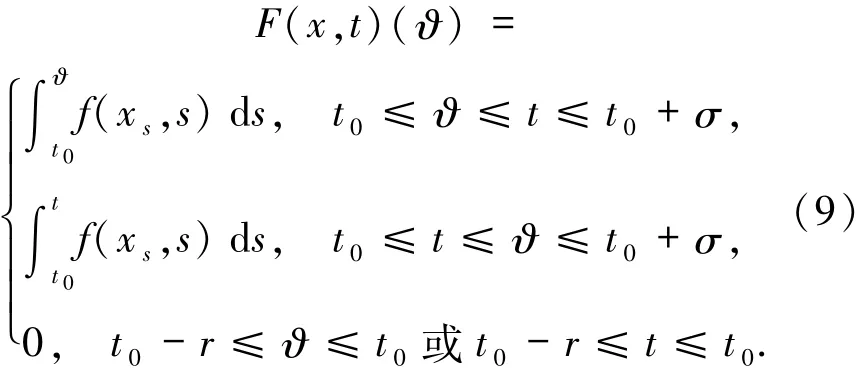
（ii）相反地，如果x（t）是方程（8）的一个解，且F由（9）式给出，在区间［t0-r，t0+σ］上满足初始条件对任意ϑ∈［t0-r，t0+σ］，定义

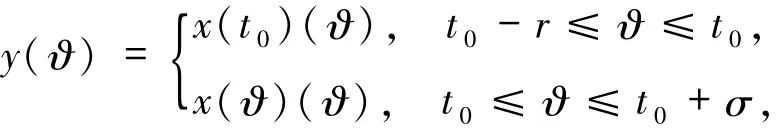
则y（ϑ）是方程（7）在［t0-r，t0+σ］上的一个解，且

y（ϑ）＝x（t0+σ）（ϑ）， ϑ∈［t0-r，t0+σ］．

注2引理1．7的详细证明过程见文献［10］中的定理3．4和定理3．5．

2 主要结果

考虑广义常微分方程

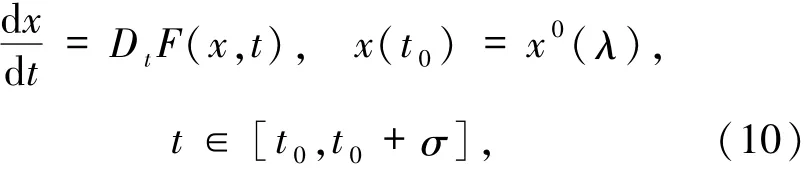
其中解x∈G1，且函数x0：Rl→Rn表示初始条件关于参数λ∈Rl的依赖性，F：G1×［t0-r，t0+σ］→Rn．

设x（s，λ）是解在s∈［t0，t0+σ］处的值．文献［7］证明了方程（10）的右端函数F关于x可微时，x（s，λ）关于λ是可微的．利用Kurzweil积分的定义，x（s，λ）的值由

逼近，其中t0＜t1＜…＜tk＝s是区间［t0，s］的一个精细分划，且

逼近．上式是

的一个逼近．因此，由文献［7］中定理4．1知，导数Z（t）＝xλ（t，λ0）是广义常微分方程

的唯一解．

定理2．1设

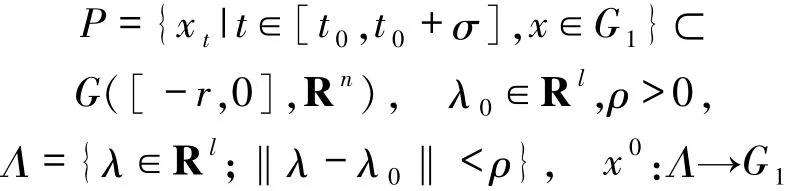
且x0在λ0处可微，f：P×［t0，t0+σ］→Rn是连续函数，其导数f x存在且在P×［t0，t0+σ］上连续，并且满足条件（A）和（B）．对任意的λ∈Λ，方程（1）在［t0，t0+σ］上有一个解，令x（t，λ）是解在t∈［t0，t0+σ］上的值，则对所有的t∈［t0，t0+σ］，函数在λ0处一致可微，其导数

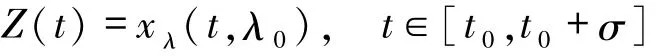
是滞后型泛函微分方程

的唯一解．

证明根据假设，对每个x，y∈G1，t∈［t0，t0+σ］，存在正常数A1、A2，使得

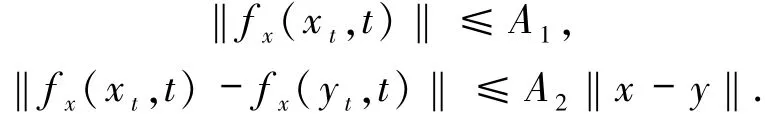
由引理1．7，对任意的λ∈Λ，方程（1）等价于广义常微分方程

其中F由（9）式给出，F正则且关于第二个变元左连续，且满足下列条件：

1）对每个固定的t∈［t0，t0+σ］，函数xF（x，t）在G1上连续可微；

2）函数x0在λ0处可微．

由条件1）知

根据文献［7］中的引理5．1（其中g（s）＝s）的结论2，有

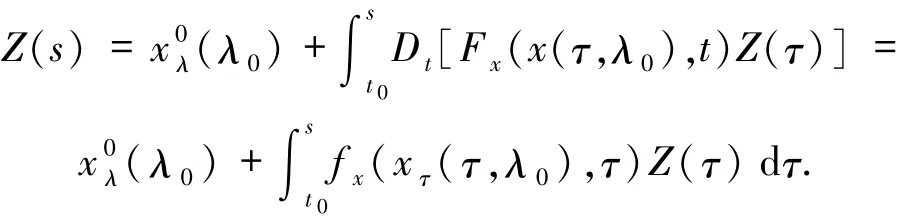
根据F由（9）式给出

对于任意的

由G1中所定义的范数可得：

则有

及

即

其中

由假设，存在常数A3＞0，使得

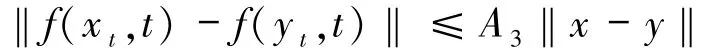
成立，则

对每个x，y∈G1，t∈［t0，t0+σ］及不减左连续函数k：［t0，t0+σ］→R，令k（t）＝A3t，则

对任意的λ∈Λ，s∈［t0，t0+σ］，根据假设，有

由

及引理1.3可知，在区间［t0，t0+σ］上，每个解x都是正则的左连续函数.如果Δλ∈Rl使得‖Δλ‖＜ρ，则

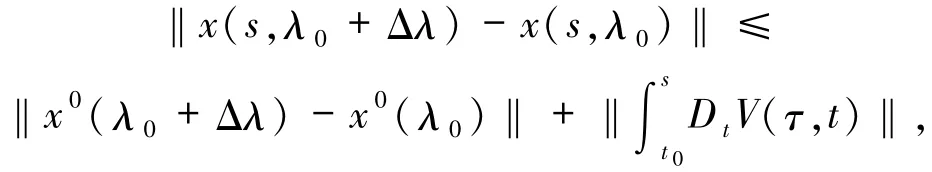
其中

通过（16）式可得

由引理1.2可得

对任意的s∈［t0，t0+σ］.利用引理1.6，则有

从而，对所有s∈［t0，t0+σ］，当Δλ→0时，x（s，λ0+Δλ）一致收敛于x（s，λ0）.令

由（14）和（15）式知

且A（τ，t）满足（6）式.由引理1.4和引理1.5可知，方程（12）有唯一解

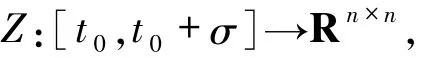
且Z是正则的，从而存在常数K＞0，使得对任意的t∈［t0，t0+σ］，有‖Z（t）‖≤K.

对任意的Δλ∈Rl，当‖Δλ‖＜ρ时，令

下证对所有r∈［t0，t0+σ］，若Δλ→0，则ξ（r，Δλ）一致趋于0.

对任意的ε＞0，存在δ＞0，使得Δλ∈Rl，‖Δλ‖＜δ时，有

及

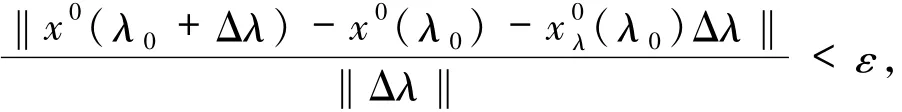
从而

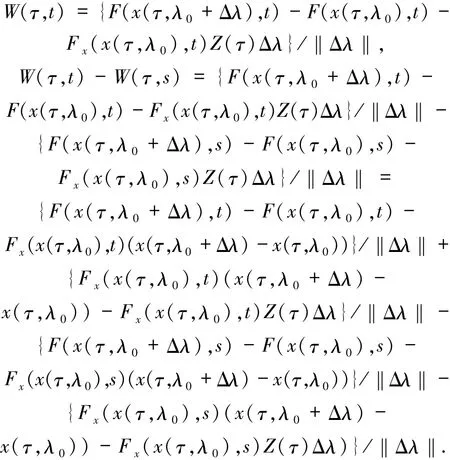
其中由于函数F在G上相对于x是连续可微的，则1

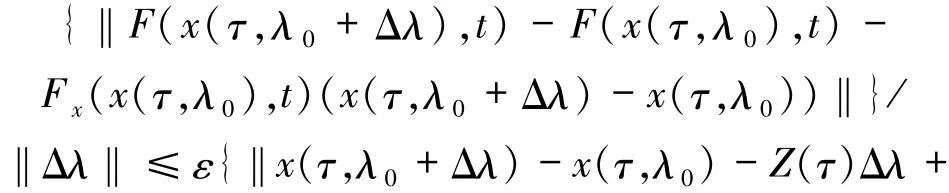
从而

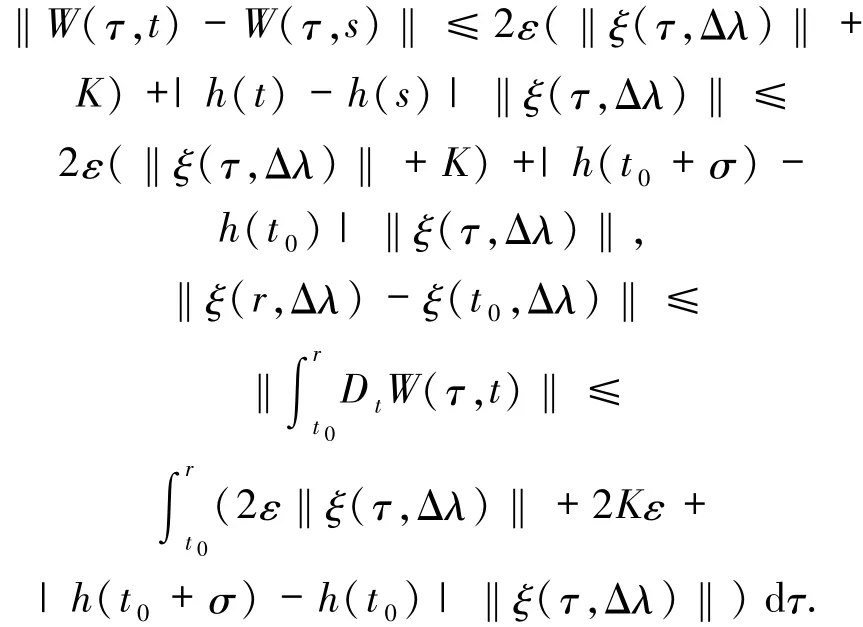
利用三角不等式得

最后，由引理1.6可得

因为ε→0+，对所有r∈［t0，t0+σ］，当Δλ→0时，ξ（r，Δλ）→0.证毕.