关于丢番图方程X2-（a2+1）Y4＝k2-1-2ka

管训贵

（泰州学院数理学院，江苏泰州225300）

1 序言及主要结论

设D、Q为给定的正整数，且D为非平方数，N（D，Q）表示方程

的正整数解的个数.

几十年前，Ljunggren［1-2］用p-adic方法，通过特殊技巧，证明了N（2，1）＝2，且（1）式有正整数解（X，Y）＝（1，1），（239，13）以及N（5，4）＝1.

最近，Stoll等［3］证明了N（22m+1，22m）≤3，文献［4-5］分别证明了N（a2+1，2a）≤3，N（a2+p2n，p2n）≤2（a、n为正整数，p为奇素数，gcd（a，p）＝1，且使方程x2-Dy2＝-1有一组整数解），N（a2+4p2n，4p2n）≤2（a、n为正整数，p为素数，gcd（a，2p）＝1，且使方程x2-Dy2＝-1有一组整数解，而方程u2-Dv2＝4无互素的整数解）；管训贵［6-8］分别证明了N（a2+1，4a-3）≤5，N（a2+1，6a-8）≤4，以及N（a2+1，12a-35）≤4.

本文将文献［6-8］和文献［4］的结果加以推广，得到更一般的结论.

定理 若a、k为正整数，满足a＞1 270k4，k≥4，则方程

除（X，Y）＝（a-k，1），以及4a2-2ka+1和2ka+1为平方数外，最多只有2组互素的正整数解（X，Y）.

作为定理的应用，有如下结论.

推论 设a为正整数，对于方程

（i）当a＝1时，仅有正整数解（X，Y）＝（3，1），（13，3）；

（ii）当a＝2时，仅有正整数解（X，Y）＝（2，1）；

（iii）当a＝3时，仅有2组互素的正整数解（X，Y）＝（1，1）和（79，5）；

（iv）当a＝4时，无正整数解（X，Y）；

（v）当a≥5时，若8a+1非平方数，则除（X，Y）＝（a-4，1）外，最多还有2组互素的正整数解（X，Y）；若8a+1为平方数，则除（X，Y）＝（a-4，1）和（8a2+a+4，（8a+1）1／2）外，最多还有2组互素的正整数解（X，Y）.

2 预备知识和引理

设α、β和γ为复数，且γ≠0或负整数.超几何函数F（α，β，γ，z）定义为复变量z的幂级数，即

令Y（ω）＝F（-5／4，-1，3／4，ω），X（ω）＝ωY（ω-1），并用Ln表示X（ω）和Y（ω）的系数的最小公分母，Hn表示

的系数分子的最大公因数.若A和B为非零整数，D为正整数，满足

则A4和B4显然为域上的代数整数.又令

且C1和f为实数，满足0＜C1＜1.25，以及

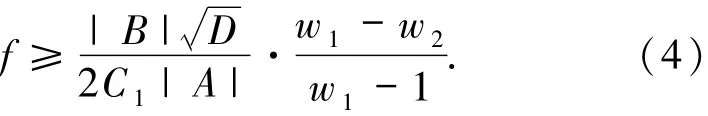
假定η、p和q为中的非零代数整数，且使得η∈｛±1，±i｝，以及

那么由（4）和（5）式及ω2＜1得定义r0为满足的正整数.于是得出引理1.

引理1设η、p和中的非零代数整数，有：

（ii）若η＝±1，则

（iii）若r0＝1，且η-1qB4≠pA4，η＝±1，则

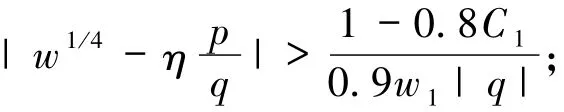
（iv）若r0＝1，且ηqB4＝pA4，η∈｛±1，±i｝，则

证明（i）由Y（w）＝F（-5／4，-1，3／4，w）＝1+5w／3，X（w）＝wY1（w-1）＝5／3+w，L4＝3以及H4＝8知

（ii）、（iii）和（iv）的证明参见文献［5］的引理2.3.

借助文献［6］中的引理2.4和引理2.5，可证下列引理.

引理2设k为正整数，a≥8.5k2为整数，则方程x2-（a2+1）y2＝k2-1-2ka（6）的所有互素的整数解由

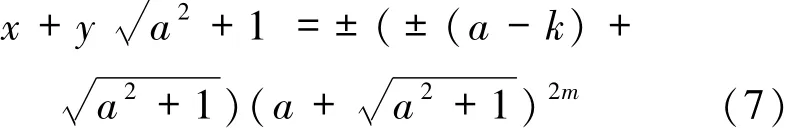
给出，这里m为整数为Pell方程x2-（a2+1）y2＝-1的基本解.

证明设（x，y）为方程（6）的一组互素的正整数解，则当a≥8.5k2时，x2＝（a2+1）y2-（2ka-a+1.由（6）式可得

故

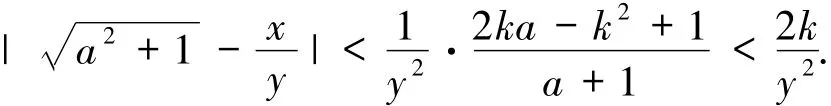
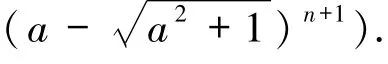
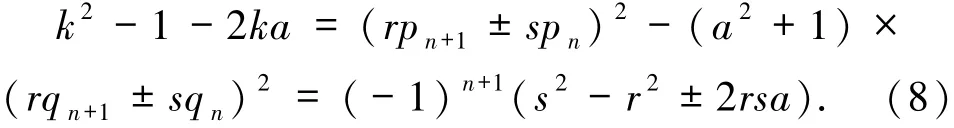
1）若n＝2n0，则（8）式成为

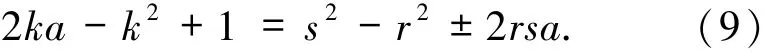
当（9）式中“+”号成立且k≠rs时，有

与a≥8.5k2矛盾.当（9）式中“-”号成立时，有

由于2（k+rs）a＞2ka≥17k3，s2-r2+k2-1＜17k2-1，故（11）式不成立.于是（9）式中“+”号成立，且k＝rs.此时（9）式成为r2s2+s2-r2-1＝0，即（r2+1）（s2-1）＝0，故s＝1，r＝k，从而有

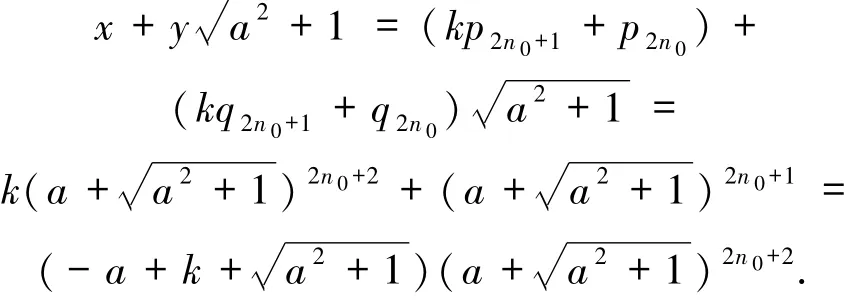
2）若n＝2n0+1，则（8）式成为

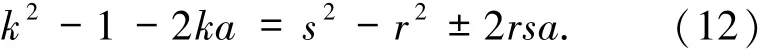
仿1）的讨论知，（12）式中“-”号成立且k＝rs.此时（12）式成为r2s2-s2+r2-1＝0，即（r2-1）（s2+1）＝0，故r＝1，s＝k.从而有

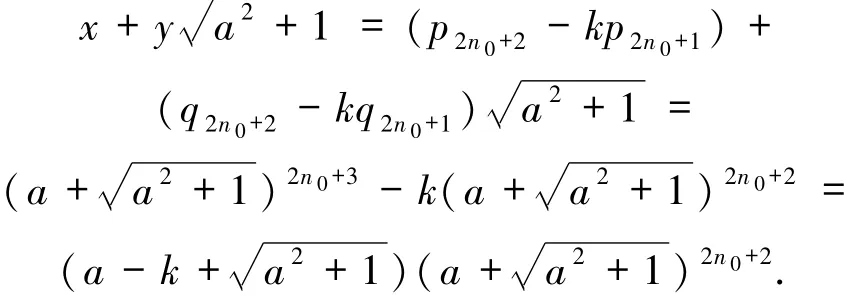
因此，当a≥8.5k2时，方程（6）的所有互素的整数解由（7）式给出.证毕.

完全类似文献［6］中引理2.7-2.9和引理2.11的证明，可得引理3-6.

引理3设D＝a2+1，Q为正整数满足D-Q＝l2（l为正整数），若方程x2-Dy2＝-Q的所有互素的整数解（x，y）由

以及某些整数m给出，并且（X，Y）≠（l，1）为方程

的一组互素的正整数解，则：

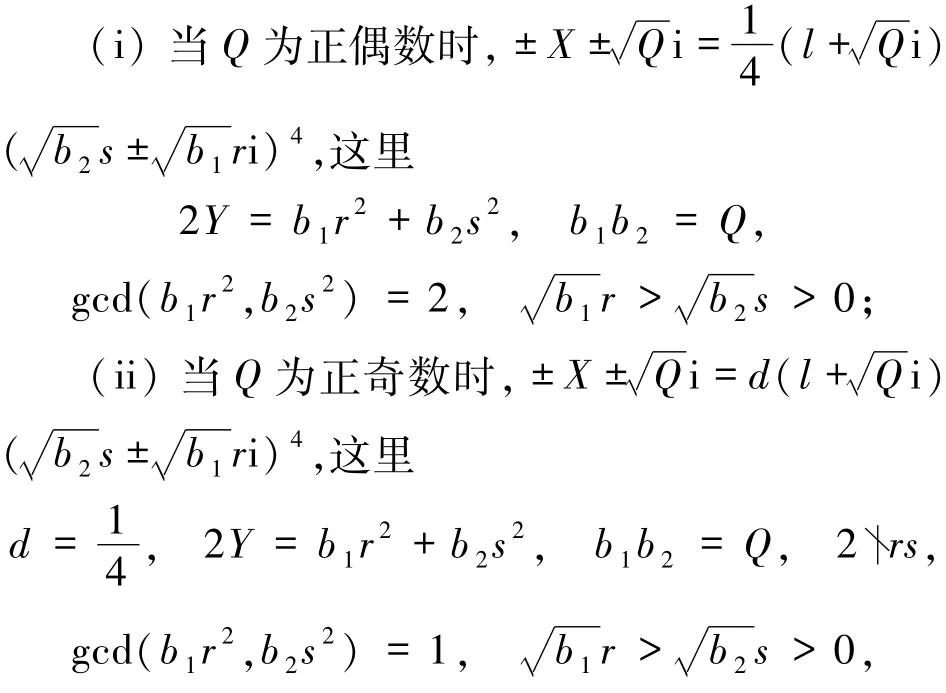
或

引理4若（X，Y）≠（l，1）为方程（13）的一组互素的正整数解，则有正整数x、y和g使得g2＜Q，且

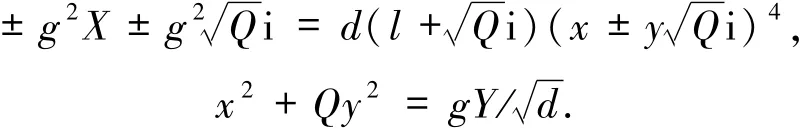
这里Q为正偶数时，d＝1／4；Q为正奇数时，d∈｛1／4，1｝.

引理5设K和l是正整数，η∈｛±1，±i｝，0＜cl＜1为常数若

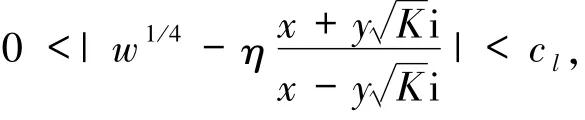
则

引理6设a＞k.若（X，Y）为方程（2）的一组互素的正整数解，Y2＝T2h±（a-k）U2h，h＞1，则：

（i）h＝2时，Y2＞8ka3，且

T4-（a-k）U4＝8ka3+4a2+4ka+1，

下证引理7.

引理7 设a＞k≥4，Q＝2ka-k2+1，若（Xj，Yj）（Yj＞1，j＝1，2，3）为方程（2）的3组互素的正整数解，则存在j1，j2∈｛1，2，3｝，使得

证明 因a＞k，即a≥k+1，故1.由引理4知，存在正整数xj、yj和gj使得3），且

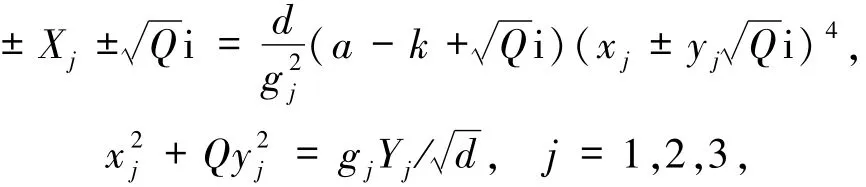
这里Q为正偶数时，d＝1／4；Q为正奇数时，d∈｛1／4，1｝.

只讨论d＝1／4时，有

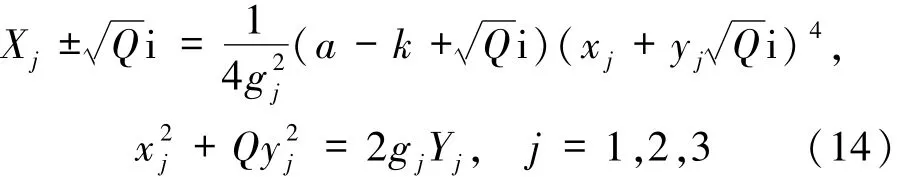
的情形，其他情形类似.此时有

设f（a）＝Q／（a2+1）＝（2ka-k2+1）／（a2+1），则

于是有

令ηj∈｛±1，±i｝满足由（16）式可证先有

首

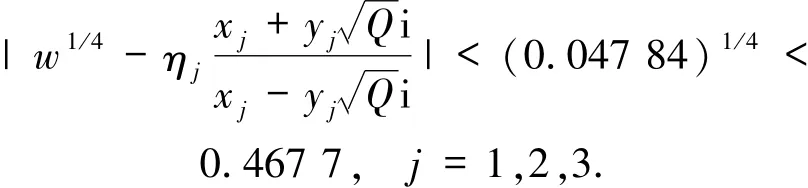
令c1＝0.467 7，则由引理5以及（2-0.467 7）可得

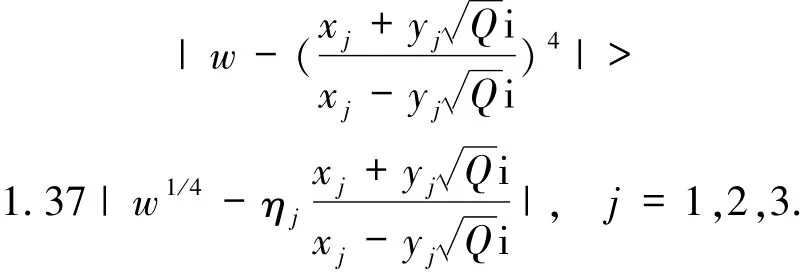
结合（16）式有

重复上述过程可得

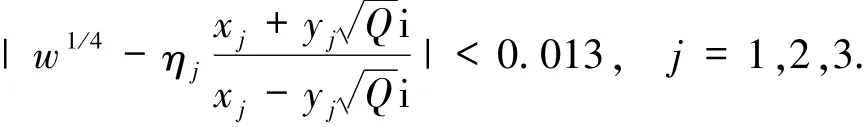
因此

结合（16）式中的第一式得

由于ηj∈｛±1，±i｝，所以存在j1，j2∈｛1，2，3｝使得ηj1／ηj2＝±1.不失一般性，假定j1＝1，j2＝2及Y2＞Y1，则有

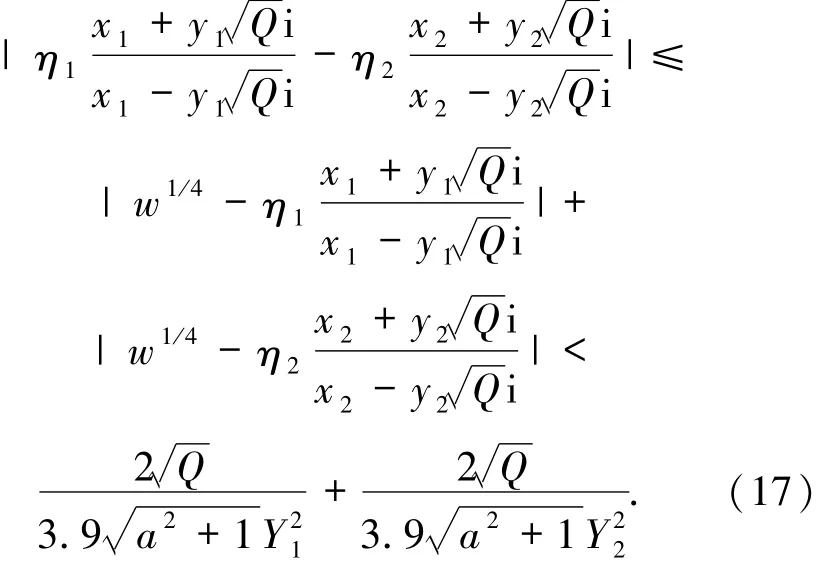
下面证明如果

那么

结合（14）式有

比较（19）式两边的虚部可得Y1＝Y2.这与Y2＞Y1相矛盾.

此外，由η1／η2＝ ±1知2｜（η1-η2）u-从而（18）式成立.

由（17）和（18）式以及Y2＞Y1≥6，有

结合Y2≥7，g1g2＜Q可得

因此

证毕.

引理8设a＞k≥4，Q＝2ka-k2+1.若（Xj，Yj）（j＝1，2，3）为方程（2）满足

的3组互素的正整数解，则存在2组互素的正整数解，不妨设为（X1，Y1），（X2，Y2），Y2＞Y1，使得η1／η2＝±1，且

证明假设（X1，Y1）和（X2，Y2）是方程（2）的两组互素的正整数解，Y2＞Y1，η1／η2＝±1，Y21＝T2h±（a-k）U2h，h＞1.根据引理4有

这里Q为正偶数时，d＝1／4；Q为正奇数时，d∈｛1／4，1｝.只讨论d＝1／4时，有

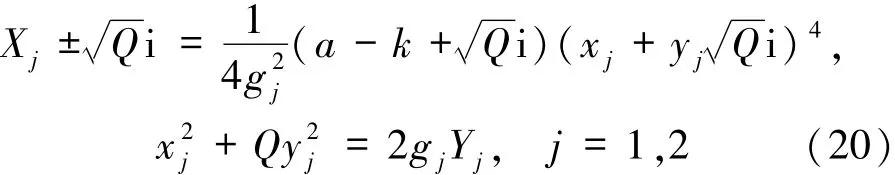
的情形，其他情形类似.此时有

由（20）式可知

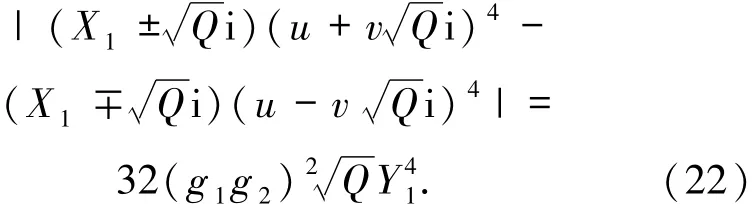
根据引理1的（ii），可令C1＝1.由引理6知，若hj＝2，则当a≥11，k≥4时，ε1＞2X1＞16ka4≥16×4×114＝937 024；若hj≥3，由于a＞k≥4，有ε1＞2X1＞64ka6≥64×4×56＝4×106＞937 024.因此

而有

故

此外，由（22）式和引理6，有

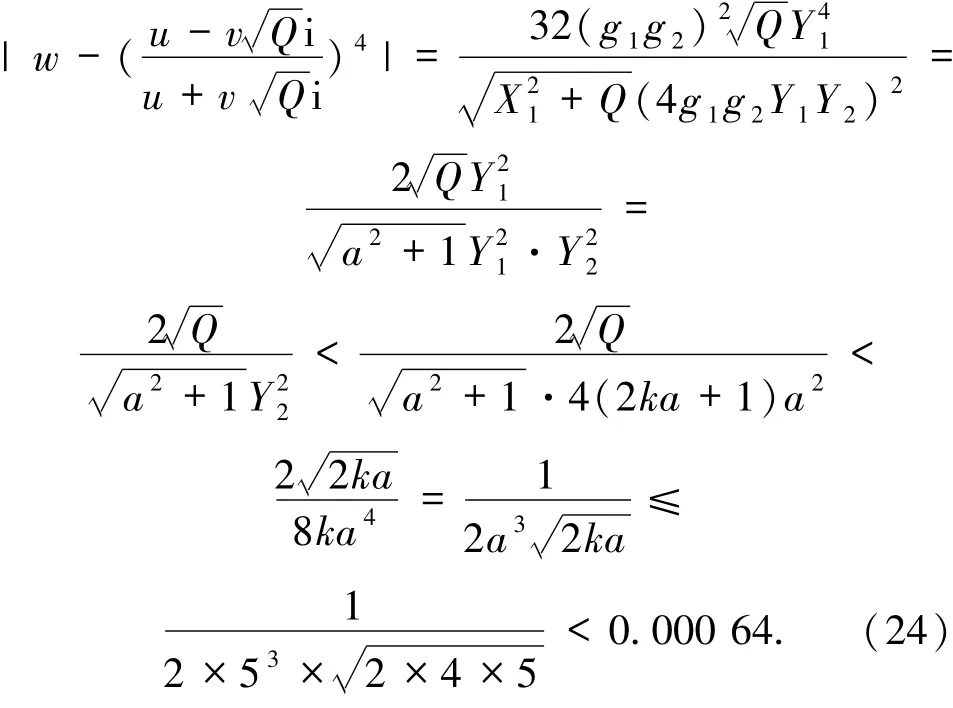
令ζ1∈｛±1，±i｝，使得

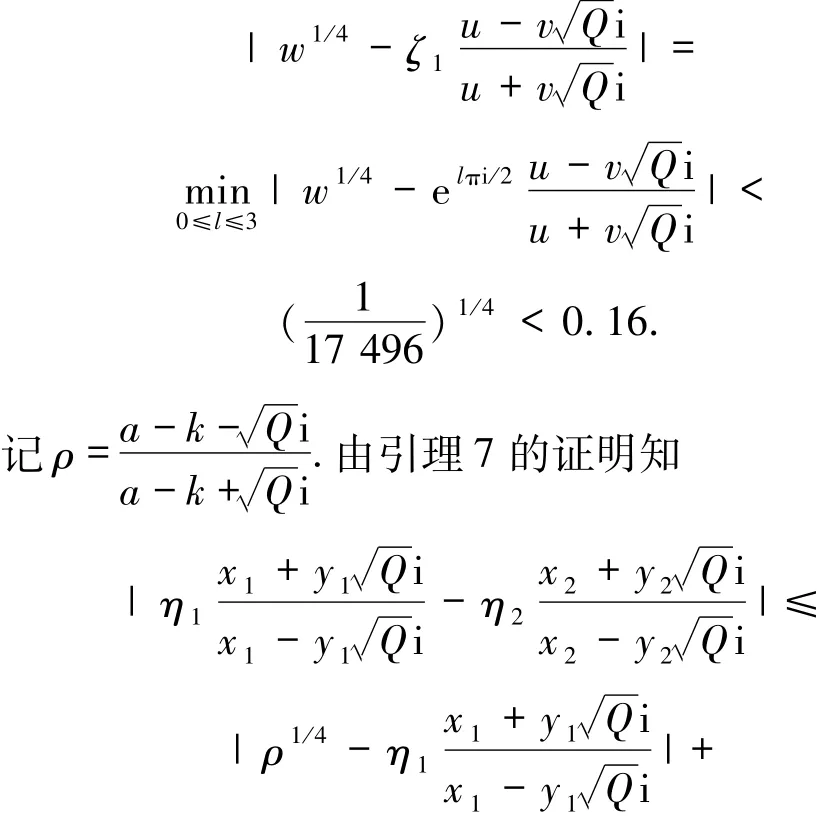
因此

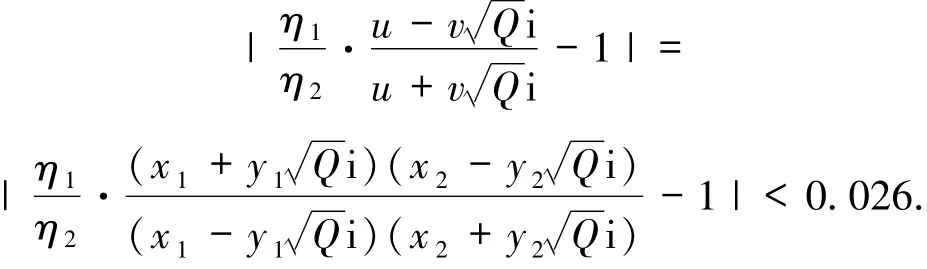
由引理6知

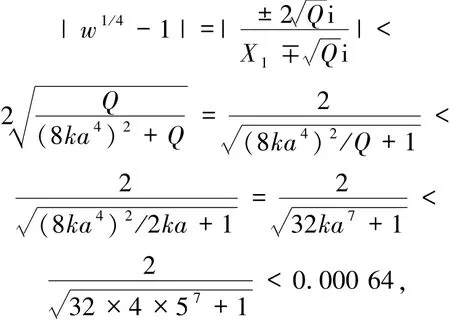
故

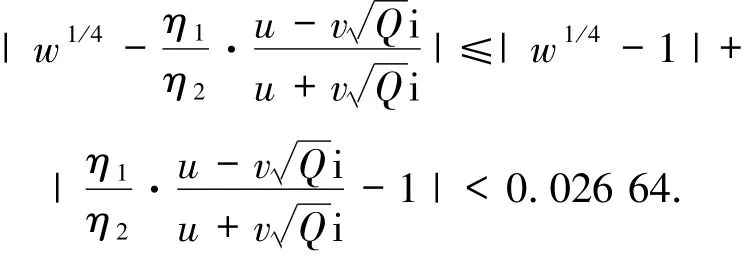
若ζ∈｛±1，±i｝，ζ≠ζ1，ζ1＝η1／η2＝±1，则

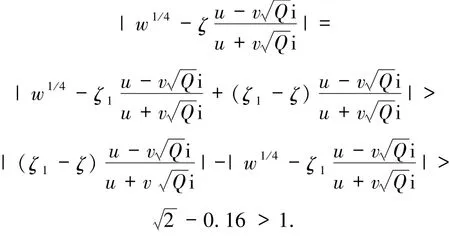
依据引理7类似的方法处理可得-

结合（23）（25）式，有

即

证毕.

3 定理的证明

设a＞k，Q＝2ka-k2+1.假定（Xj，Yj）（j＝1，2，3）为方程（2）的3组互素的正整数解，满足

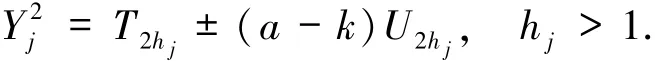
由引理7知，存在2组互素的正整数解，不失一般性，设为（X1，Y1），（X2，Y2），Y2＞Y1，使得η1／η2＝±1，且若得出矛盾，则意味着方程（2）最多有2组互素的正整数解（X，Y）满足h＞1.由引理1的（i）知

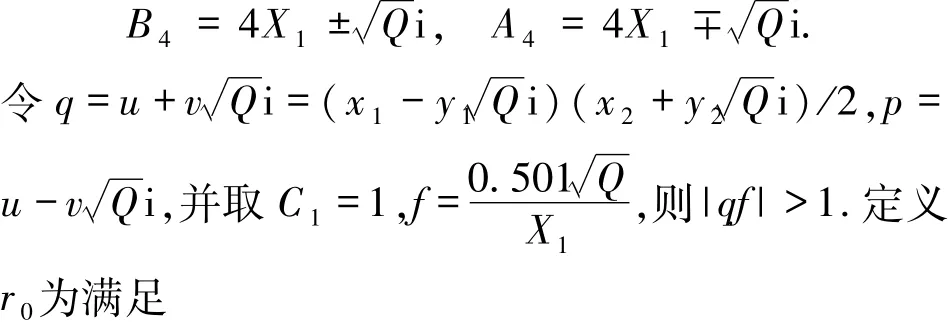
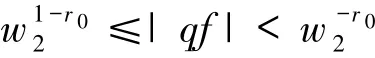
的正整数.我们分3种情形讨论（只考虑d＝1／4的情况）.

情形1r0＝1及此时由引理1的（iii）知

因此

由引理7知

若h≥3，则当a＞k≥4时，由引理6知，Y2＞32ka5＞189k4a，与（26）式矛盾.

若h＝2，则当a＞4.87k3／2时，由引理6知Y2＞8ka3＝8ka2·a＞8k（4.87k3／2）2·a＞189k4a，也与（26）式矛盾.

情形2r0＝1，ηqB4＝pA4以及η∈｛±1，±i｝.此时

令gcd（X1，Q）＝l，由gcd（X1，Y1）＝1知l｜（a2+1），故l｜2k（a2+1）-aQ＝（k2-1）a+2k，从而l｜2k（（k2-1）a+2k）-（k2-1）Q＝（k2+1）2.进一步有

因此，由（27）式及引理4可得

又由引理1的（iv）知

于是

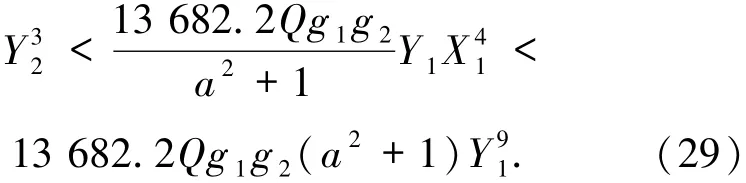
由g1g2＜Q，并结合（28）和（29）式得

若h≥5，则当a＞k时，由引理6知，Y2＞512ka9＞与（30）式矛盾.

若h＝4，则当a＞1.002k49／43时，由引理6知，

也与（30）式矛盾.

若h＝3，则当a＞1.32k49／31时，由引理6知，

仍与（30）式矛盾.

若h＝2，则当a＞2.41k49／19时，由引理6知，

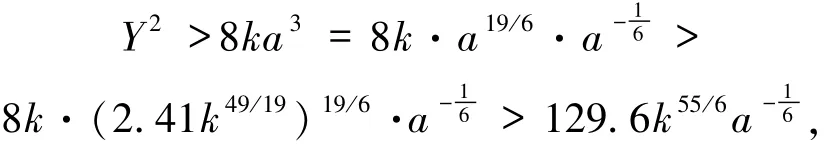
同样与（30）式矛盾.

情形3r0＞1.由r0的定义知，w2｜qf｜≥1，故＜

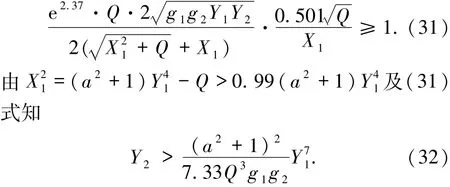
根据引理8，结合（32）式和g1g2Q，可得

若h≥5，则当a＞k≥4时，由引理6知，Y2＞512ka9＝512k·53·k4·a2＝64 000k5a2，与（33）式矛盾.

若h＝4，则当a＞2.4k0.8时，由引理6知，Y2＞128ka7＝128ka5·a2＞128k（2.4k0.8）5·a2＞10 192k5a2，也与（33）式矛盾.

若h＝3，则当a＞6.821k4／3时，由引理6知，Y2＞32ka5＝32ka3·a2＞32k（6.821k4／3）3·a2＞10 155k5a2，仍与（33）式矛盾.

若h＝2，则当a＞1 270k4时，由引理6知，Y2＞8ka3＞8k·1 270k4·a2＝10 160k5a2，同样与（33）式矛盾.

最后，需要讨论h＝1的情形.

假定（X，Y）≠（a-k，1）为方程（2）的一组互素的正整数解，满足Y2＝T2±（a-k）U2，则Y2＝2a2+1±（a-k）·2a，故有Y2＝4a2-2ka+1及Y2＝2ka+1.

综上，若a＞1 270k4，（X，Y）≠（a-k，1），则方程（2）除开4a2-2ka+1和2ka+1为平方数外最多只有2组互素的正整数解（X，Y）.定理得证.

说明 由定理的证明不难看出，欲将定理中的条件“a＞1 270k4”加强为“a＞k”，只需证：

1）当k＜a＜8.5k2时，方程（6）的所有互素的整数解由（7）式给出.

2）当k＜a≤max｛2.4k0.8，1.002k49／43｝时，T8±（a-k）U8为非平方数；

当k＜a≤max｛1.32k49／31，6.821k4／3｝时，T6±（a-k）U6为非平方数；

当k＜a≤1 270k4时，T4±（a-k）U4为非平方数.

4 推论的证明

（i）当a＝1时，方程（3）成为

运用递归序列、同余式和平方剩余的初等方法可证明方程（34）仅有正整数解（X，Y）＝（3，1）和（13，3）.

（ii）当a＝2时，方程（3）成为

根据文献［9］的第79页定理3，方程（35）仅有正整数解（X，Y）＝（2，1）.

（iii）当a＝3时，方程（3）成为

这是文献［5］的定理1.3中a＝n＝1，p＝3的情形.考虑到（X，Y）＝（1，1），（79，5）适合方程（36），且方程x2-10y4＝-1有一组整数解（x，y）＝（3，1），故方程（36）仅有2组互素的正整数解（X，Y）＝（1，1），（79，5）.

（iv）当a＝4时，方程（3）成为

易知，17｜X.令X＝17X1，则得由文献［10］第七章第一节定理知，该方程无正整数解（X1，Y），从而方程（37）无正整数解（X，Y）.

（v）当a≥5时，考虑到k＝4，证明：

1）4＜a＜136的情形下，方程（6）的所有互素的整数解由（7）式给出.

根据引理2的证明，rs＜16.

若n＝2n0，则

由（38）式知，s、r为一奇一偶，故

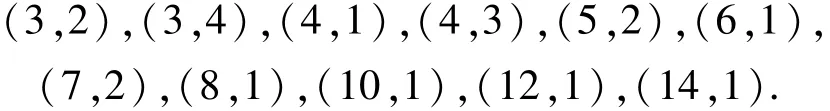
经验证知：（s，r）＝（1，4），（1，6），（1，8），（1，10），（1，12），（1，14），且取“+”号.

当（s，r）＝（1，4）时，a为任意正整数，此时

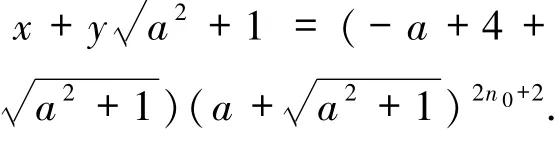
当（s，r）＝（1，2m）（m≠2）时，由（38）式得a＝m+2.此时

若n＝2n0+1，则

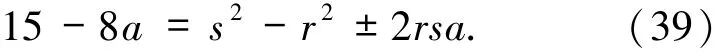
经验证知：（s，r）＝（4，1），（6，1），（8，1），（10，1），（12，1），（14，1），且取“-”号.

当（s，r）＝（4，1）时，a为任意正整数.此时

当（s，r）＝（2m，1）（m≠2）时，由（39）式得a＝m+2.此时

2）当4＜a≤max｛2.4×40.8，1.002×449／43｝时，a＝5，6，7，此时T8-（a-4）U8＝43 490 761，73·444 487，442 394 569，T8+（a-4）U8＝13·4 977 757，739·408 427，1 109·986 837皆非平方数；同样，由Maple 9.5计算知，当4＜a≤max｛1.32×449／31，6.821×44／3｝，即5≤a≤43时，T6±（a-4）U6皆非平方数；当4＜a≤1 270×44，即5≤a≤325 120时，T4±（a-4）U4皆非平方数.

3）若4a2-8a+1＝M2（M为正整数），则得a＝2，与a≥5矛盾.因此推论得证.

致谢泰州学院教博基金（TZXY2018JBJJ-002）对本文给予了资助，谨致谢意.