基于对偶四元数的捷联惯导算法在发射点惯性系下的应用研究

杜 鹏，杨 静，邱红专，熊 凯

(1.北京航空航天大学自动化科学与电气工程学院，北京 100083；2. 北京控制工程研究所，北京 100081)

0 引言

对于运行在高动态环境下的载体而言，捷联惯性导航系统的性能容易受恶劣环境的影响，在姿态解算的过程中，由于有限转动的不可交换性，不可避免地存在着由圆锥运动引起的圆锥误差；在速度解算的过程中，由于运载体同时存在线运动和角运动，当采用速度增量进行解算时，也必须考虑到系统的划船误差的影响。传统的捷联惯导算法通过对圆锥误差和划船误差分别设计相应的算法进行补偿来提高算法的精度[1]。文献[2-3]针对速度解算中产生的划船误差，在东北天导航坐标系下设计了不同的算法进行补偿。而针对姿态解算中产生的圆锥误差，文献[4-6]针对不同的陀螺设计了基于角增量和角速度的圆锥效应补偿算法。

在传统的导航算法中，对划船误差和圆锥误差分别设计算法进行补偿，采用了传统的运动学观点，将刚体的旋转与平移分开进行考虑。而对于刚体来说，旋转与平移实际上是同时进行的，有学者提出了可以利用相关公式将圆锥补偿算法转换为划船误差补偿算法[7-9]，但这并不容易在实际的导航算法中实现，而研究发现划船误差补偿算法与圆锥误差补偿算法存在一定的等价性，其补偿原理和过程大致相同。而由Clifford在对偶数基础上提出的对偶四元数，提供了一种可以同时描述旋转和平移的工具。文献[10]将对偶四元数应用于惯性导航解算，推导了更为简单直观的基于对偶四元数的惯导微分方程。

对偶四元数导航算法能同时对划船误差与圆锥误差进行补偿，可以在一定程度上提升导航算法的性能。目前已公开发表的文献大多是以飞机等载体为对象，在东北天导航坐标系下对对偶四元数导航算法展开研究的[11]；而运行在高动态环境下的弹道导弹等载体，通常采用发射点惯性坐标系作为导航坐标系，相关研究并不多见。本文将在发射点惯性系下，对基于对偶四元数的捷联惯导算法展开研究。

论文的结构安排如下，首先介绍了发射点惯性系下的捷联惯导解算模型，在此基础上推导了发射点惯性坐标系下对偶四元数算法的解算公式，比较了速度更新过程中对偶四元数算法与传统算法的精度差异。并设计了多条机动飞行轨迹，以三子样算法为例，对对偶四元数算法和传统算法的性能进行了仿真对比分析。

1 发射点惯性系下捷联惯导解算

1.1 坐标系说明

将文中用到的主要坐标系定义如下：

1)发射点惯性坐标系oxliylizli：坐标原点位于初始时刻的发射点；oxli轴是发射垂直面与发射点当地水平面的交线；oyli轴垂直于oxli轴，指向天；ozli轴与oxli轴、oyli轴垂直；且oxliylizli构成右手定则，在惯性空间保持不变，以下简称发射点惯性系。

2)载体坐标系oxbybzb：坐标原点位于载体质心；oxb轴与载体纵轴一致，指向机头方向；oyb轴垂直于oxb轴，位于载体纵对称面内，指向上方；ozb轴与oxb轴、oyb轴构成右手定则。

3)地心惯性坐标系oxcyczc：地球坐标系oxeyeze在发射瞬时所固定的坐标系。

1.2 解算方法

在发射点惯性系下，建立捷联惯导的微分方程如下

(1)

(2)

(3)

根据上述发射点惯性下的捷联惯导微分方程，利用加速度计测量的比力和陀螺测量的角速度，分别通过速度更新和位置更新、姿态更新两个主要环节可以实现对导航参数的递推解算。

1)速度和位置更新

通过求解式(1)和式(2)实现速度和位置的更新。为此，需要将载体坐标系下的比力转换到发射点惯性系下

(4)

求解重力加速度在地心惯性系下的分量

(5)

(6)

(7)

由式(4)和式(5)可以计算得到发射点惯性系下的加速度

(8)

对式(8)积分就可以解算出速度和位置

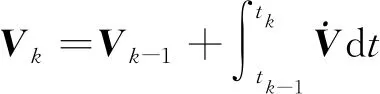
(9)

2)姿态更新

根据描述姿态方式的不同，姿态更新算法有欧拉角法、方向余弦法和四元数法。由于四元数法算法简单、计算量小、无奇点，因此，在姿态更新中得到了广泛应用。对式(3)求解就可以对四元数进行更新。

在开始进行姿态更新时，需要对四元数进行初始化，这里可以利用载体在初始状态下的欧拉角初值来解算四元数初值。

若载体三次转动对应的欧拉角顺序是俯仰角φ0、航向角ψ0和滚转角γ0，即载体从发射点惯性系到载体坐标系的转动过程如下

由此可以得到由欧拉角表示的发射点惯性系到载体系的姿态转换矩阵为

(10)

对应的四元数的初值为

q1=cos(γ0/2)cos(ψ0/2)cos(φ0/2)+

sin(γ0/2)sin(ψ0/2)sin(φ0/2)

q2=sin(γ0/2)cos(ψ0/2)cos(φ0/2)-

cos(γ0/2)sin(ψ0/2)sin(φ0/2)

q3=cos(γ0/2)sin(ψ0/2)cos(φ0/2)+

sin(γ0/2)cos(ψ0/2)sin(φ0/2)

q4=cos(γ0/2)cos(ψ0/2)sin(φ0/2)-

sin(γ0/2)sin(ψ0/2)cos(φ0/2)

(11)

对微分方程进行求解就可以对四元数进行更新。

2 基于对偶四元数的捷联惯导算法

当载体处在高动态的环境中时，由于有限转动的不可交换性，在姿态解算中不可避免地存在着由圆锥运动引起的圆锥误差；在速度解算的过程中，也必须考虑到系统的划船误差的影响。传统的运动学观点是将两者分开进行考虑，而对偶四元数可以统一考虑圆锥误差与划船误差进行补偿。

2.1 对偶四元数

对偶数是由W.Clifford在1873年提出的，因其形式类似于复数，可以看作是复数域的扩充。其形式如下[12-14]

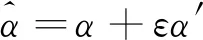
(12)

其中，α为对偶数的实数部分;α′为对偶数的对偶部分;ε为对偶数单位，且必须有：ε2=ε3=,…，0。

刚体在空间中的旋转和平移可以用图 1表示，刚体绕过点c的单位向量l旋转θ角后，沿l的方向平移距离d(或者先沿l的方向平移距离d后，再旋转θ角)。

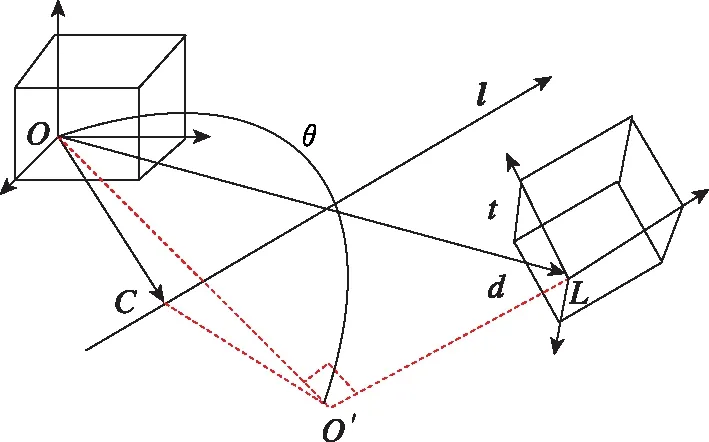
图1 刚体在空间的旋转与平移Fig.1 Rotation and translation of rigid bodies in space

刚体的这种运动类似于螺钉和螺母的运动，因此又被称为螺旋运动，可以用螺旋矢量统一表述，螺旋矢量定义为

(13)

其中，单位螺旋轴为

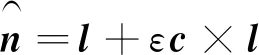
(14)

对偶角为

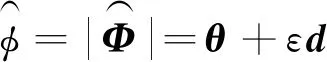
(15)

对偶四元数是以对偶数和四元数为基础的。其定义如下

(16)

其中，ε为对偶数单位，q和q′都是普通的四元数

q=q0+q1i+q2j+q3k

(17)

q′=q4+q5i+q6j+q7k

(18)

在图 1中，平移和转动分别对应以下关系

tL=q*°to°q

(19)

to=q°tL°q*

(20)

其中：to=[0,to]为零标量的四元数。

根据以上关系，对偶四元数可以表示为如下形式

(21)

其中，实部q是描述转动的规范四元数;对偶部q′是转动四元数和平移向量的函数。

对偶四元数可以由螺旋运动的参数表示为

(22)

由式(19)和式(20)可得

to=2q′°q*tL=2q*°q′

(23)

对偶四元数微分方程为

(24)

式中，对偶向量为

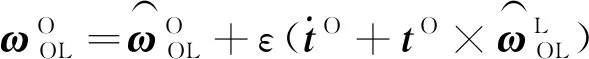
(25)

与传统四元数更新算法类似，运用螺旋矢量来更新四元数。螺旋矢量的微分方程如下

(26)

(27)

(28)

因此，式(27)可表示为

(29)

对式(29)在时间间隔[tk,tk+1]内积分得到

(30)

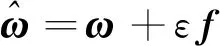
εf(τ)]dτ]×[ω(t)+εf(t)]}dt

[ω(t)+εf(t)]}dt

=Δθm+εΔVm+Φcon+εΔVsculm

(31)

式中

(32)

其中，Φcon和ΔVsculm分别代表圆锥误差和划船误差。从式(32)可以看出，对偶四元数算法将旋转和平移统一起来，能够同时补偿圆锥误差和划船误差。

与旋转矢量法类似，螺旋矢量的计算也由单子样、双子样和三子样等相应的优化算法来完成，其优化系数与等效旋转矢量法的优化系数完全相同，在得到螺旋矢量后就可以用其来更新对偶四元数。下面以三子样算法为例，给出对偶四元数的更新步骤为：

螺旋矢量三子样优化算法

(33)

步骤二：由式(22)可得

(34)

将对偶四元数实数部分和对偶部分拆开得

(35)

将得到的螺旋矢量代入式(35),计算q(ΔT)和q′(ΔT)。

步骤三：设tk+1时刻的对偶四元数可表示为

(36)

将式(36)按照定义拆分成标量部分和对偶部分得到

(37)

将得到的q(ΔT)和q′(ΔT)代入式(37),计算tk+1时刻的对偶四元数。

与东北天坐标系下对偶四元数的更新不同，在发射点惯性系下，不用再考虑地球自转的影响，也不用再利用分离坐标系的思想，所有的更新均在发射点惯性系下进行。

2.2 对偶四元数初始化

任意一种捷联惯性导航算法都要有一个迭代递推的过程,由前一时刻的导航信息推算得到当前时刻的导航信息。在传统的导航算法中，进行解算时需要知道初始时刻的三轴速度、位置及姿态角(俯仰、偏航、滚转角)。而利用对偶四元数进行解算时,需要的初始信息为同时包含平动和转动信息的初始对偶四元数。

对偶四元数实部的初始化与1.1节中姿态更新一样。

对偶四元数对偶部的初始化如下

(38)

其中，Vli(0)为初始时刻载体在发射点惯性系下的速度。

2.3 速度更新算法比较

在传统的速度更新算法中，两个时刻之间的速度增量为

(39)

对于对偶四元数来说，由式(23)可得对偶四元数更新算法的速度增量为[14]

(40)

将式(40)中的三角函数取四阶近似，并忽略高阶小量，则在对偶四元数更新算法中速度增量的计算公式如下

(41)

将式(31)代入式(41)可得

[(Δθm+Φcon)×(ΔVm+ΔVsculm)]

(42)

与式(39)相比，对偶四元数速度更新算法中速度增量的计算增加了式(42)右边的后四项，这四项说明了对偶四元数计算的速度增量更为准确，从而提高了速度更新的精度。

3 仿真验证

为了验证对偶四元数导航算法的性能，本节将设计复杂程度不同的多条机动轨迹，并在三子样条件下，对基于对偶四元数的导航算法和基于旋转矢量的传统导航算法的性能进行对比研究。为了更直观地验证采用对偶四元数对于减弱不可交换误差以提高导航精度的作用，这里暂不考虑算法中基于重力模型计算的重力分量对导航解算结果的影响。因此，在本节的仿真实验中，将重力加速度近似为常值进行测试。

(1)单轴姿态机动

在载体进行单轴姿态机动时，每次仅绕俯仰轴、偏航轴和滚转轴中的一个轴，按照一定的角速度变化规律持续做周期运动，姿态角也随之作周期性的变化，且在规定的时间内达到设定幅值θ。在单轴姿态机动(简称轨迹1)下，单周期的基本轨迹参数如表1所示，按照该参数共持续25个周期，总运行时间为1000s，导航解算周期为0.03s。

表2列出了载体分别绕俯仰轴、偏航轴与滚转轴做姿态机动，当θ分别为30°、60°和80°时的导航解算误差结果。由于纯捷联惯导算法的解算误差是随着时间累积而增大的，故表2中数据统计的是终点时刻的导航参数误差。图2～图4所示为当俯仰角变化幅值为30°时，两种解算方法的导航误差曲线。图中红线为对偶四元数导航算法的解算结果，蓝线为传统三子样算法的解算结果。

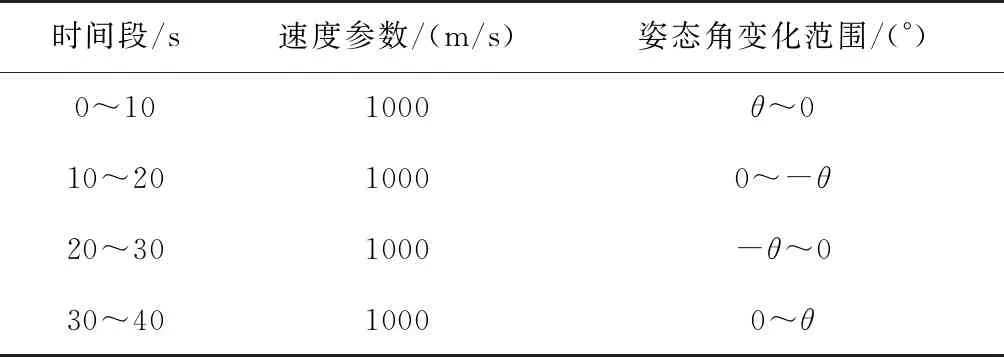
表1 轨迹1参数说明

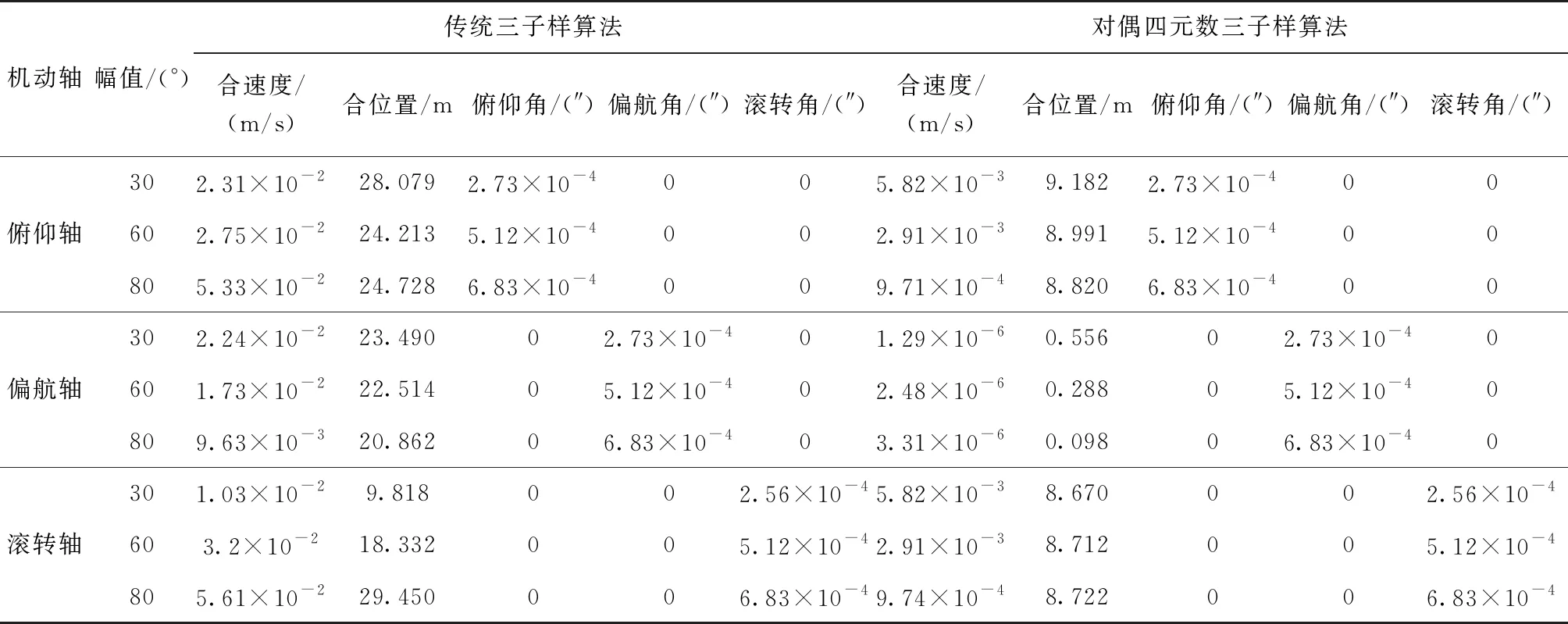
表2 载体单轴机动时导航误差

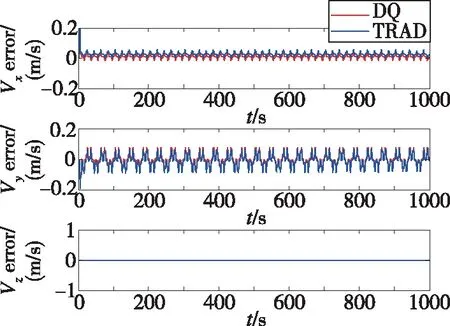
图2 速度误差(轨迹1)Fig.2 Velocity error(trajectory 1)

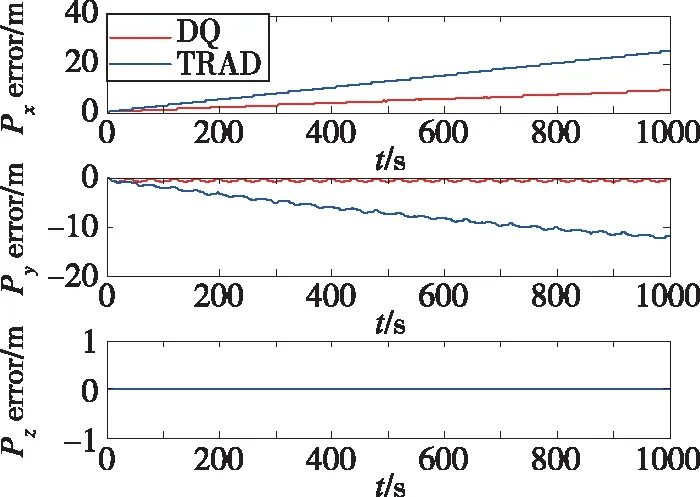
图3 位置误差(轨迹1)Fig.3 Position error(trajectory 1)

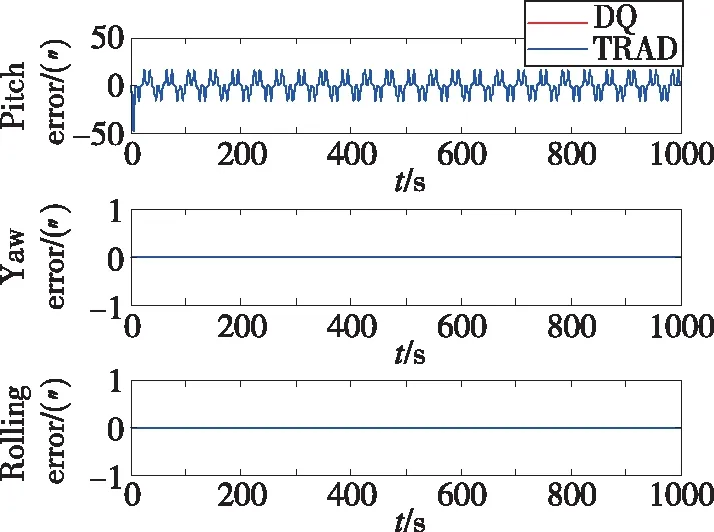
图4 姿态误差(轨迹1)Fig.4 Attitude error(trajectory 1)

由表2和图2、图3可以看出，使用对偶四元数导航算法解算的速度和位置的精度明显高于传统的三子样算法。其中位置误差由24m减小到9m左右，速度误差也减小了很多，这就验证了第2节的理论分析。从图4可以看出，两种方法解算得到的姿态误差曲线几乎重合，这说明采用对偶四元数导航算法后，姿态精度并未得到提高，这是因为两种算法采用的姿态更新原理是一样的，都是利用对偶四元数的实部即转动四元数进行姿态的解算。

以上通过单轴姿态机动的仿真实验，验证了对偶四元数算法可以有效提高单轴姿态持续机动情况下速度和位置的解算精度，但并不能提高姿态精度。

(2)三轴姿态机动

为了进一步验证对偶四元数算法在复杂机动情况下的性能，设计了三轴同时进行姿态机动的轨迹，即每次同时绕俯仰轴、偏航轴和滚转轴按照一定的角速度变化规律持续做周期运动，姿态角也随之做周期性的变化，且在规定的时间内达到设定幅值θ。在三轴复杂姿态机动(简称轨迹2)下，单周期的基本轨迹参数如表3所示，按照该参数共持续25个周期，总运行时间为1000s，导航解算周期为0.03s。

表4列出了载体按照表3中的参数进行三轴姿态机动时的终点导航误差。图5～图7所示为载体按轨迹2机动时，两种导航解算方法下的导航误差曲线对比图。图中红线为对偶四元数导航算法的解算结果，蓝线为传统三子样算法的解算结果。

表3 轨迹2说明

表4 载体三轴姿态机动时导航误差

图5 速度误差(轨迹2)Fig.5 Velocity error( trajectory 2)

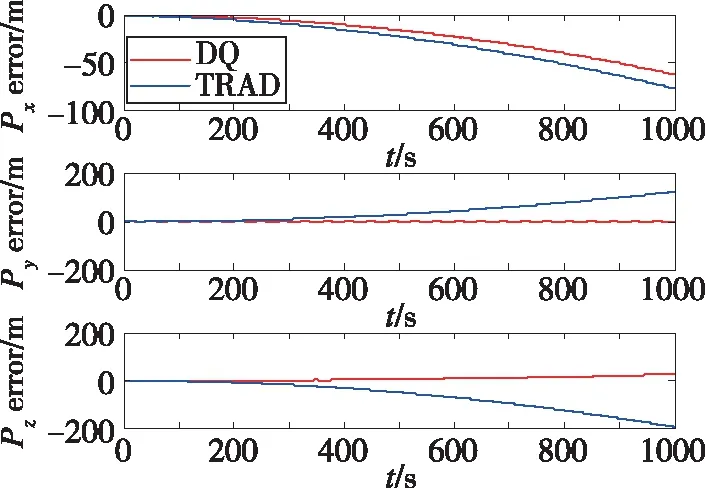
图6 位置误差(轨迹2)Fig.6 Position error(trajectory 2)

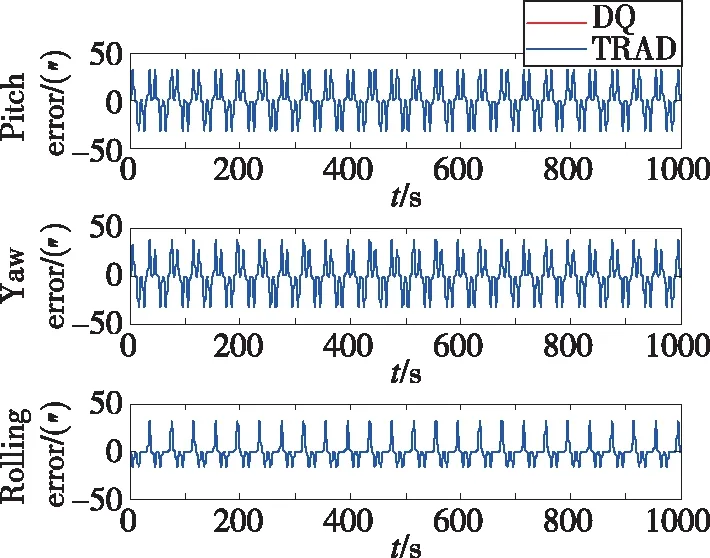
图7 姿态误差(轨迹2)Fig.7 Attitude error(trajectory 2)

由图5和图6可以看出，对偶四元数算法解算出的三轴速度和位置误差明显小于传统算法的解算结果，其中终点位置误差由240多m减小到60多m。由此可见，当载体按照轨迹2机动时，采用对偶四元数算法解算的速度和位置精度有显著提高，且随着时间的推移和机动复杂性的增加，这种精度优势更加明显。

由图7可以看出，两种算法下的姿态误差曲线几乎重合，这是由于两种算法中的姿态更新方法无本质区别，因此，对偶四元数导航算法并不能提高姿态的解算精度。

4 结论

本文以发射点惯性系为导航系的弹类载体为对象，针对弹载捷联惯性导航系统在高动态环境下容易产生圆锥误差与划船误差的问题,设计了基于对偶四元数的捷联惯性导航算法，并通过仿真实验验证了方法的有效性。通过对三子样下的基于对偶四元数的捷联惯性导航算法和传统算法的理论分析与实验结果对比分析表明：

1)对偶四元数导航算法可以同时补偿系统的圆锥误差与划船误差，速度和位置的解算精度明显高于传统算法，但姿态精度相当。

2)载体所作的机动越复杂、持续时间越长，基于对偶四元数的捷联惯导算法的精度优势越明显。