三维Helmholtz 类方程柯西问题的一种基于修正核的数值解

何尚琴 冯秀芳†

(1. 北方民族大学数学与信息科学学院，银川 750021; 2. 宁夏大学数学统计学院，银川 750021)

0 引言

近几十年来，偏微分方程不适定问题的研究受到越来越多的关注，归因于受其他学科和众多工程技术领域的广泛应用所驱动。例如，脑电图影像、电阻抗断层、光断层扫描、炼钢炉中腐蚀面的估计等方面的应用[1]。求解不适定问题的普遍方法是：用一族与原不适定问题相“邻近”的适定问题的解去逼近原问题的解，这种方法称为正则化方法。如何建立有效的正则化方法是反问题领域中不适定问题研究的重要内容。通常的正则化方法有基于变分原理的Tikhonov 正则化方法、各种迭代方法以及其它的一些正则化方法和改进方法，这些方法都是求解不适定问题的有效方法，在各类反问题的研究中被广泛运用，并得到深入研究[2]。

对于正波数的Helmholtz 方程△u+k2u=0, k ＞0 的数值解已有许多研究方法和成果[3]。纯虚波数的Helmholtz 方程△u-k2u= 0, k ＞0 称为修正的Helmholtz 方程(又称Yukawa 方程)，通常出现在半隐式时间离散的热方程中，也用来描述波的弥散、扩散问题等物理现象，国内外已有许多研究结果[4–5]。修正的Helmholtz 方程问题是一类严重的不适定问题[6]。针对此类方程Cauchy 问题的求解，目前有BEM 法[7]、Fourier 正则化方法[8]以及截断法[9]等方法。

软化方法也是求解不适定问题的一种方法，此方法用来求解不适定问题的关键是构造软化算子，很多利用软化法解决柯西问题的研究都是利用选定的核函数和测量数据做卷积，把不适定问题转化为适定问题进而求解。但是核函数的选取并不唯一，每一类核函数都有其自身的优势和特点。Manselli 和Miller[10]以及Murio[11–12]用Weierstrass 核来构造软化算子解决了热传导方程的一些不适定问题。H`ao[13]分别用de la Vall´ee Poussin 核与Dirichlet 核构造软化算子解决了一些经典的不适定问题。Murio 在文献[14]中用Gaussian 核构造软化算子解决了数值微分和逆热传导问题。文献[15–17]也用Gaussian 核研究了几类椭圆方程的柯西问题。文献[18]利用修正核的方法研究了二维热传导方程的柯西问题。本文受文献[18]启发，研究修正的Helmholtz 方程的柯西问题。在原有柯西问题解的基础上，构造修正算子，将不适定问题转化为适定问题。并在正则参数的选取之下得到了逼近解和精确解之间的L2-误差估计和Hs-误差估计。最后用数值算例验证了所提出方法的有效性和稳定性。

本文考虑如下的Cauchy 问题

1 问题不适定性分析

设ˆφ(w,η,z)表示函数φ(x,y,z)关于变量r=(x,y)∈R2的Fourier 变换[13]

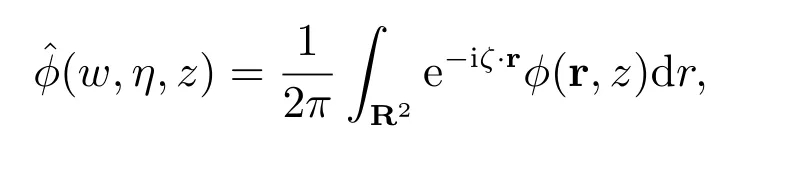
2 修正算子及正则化解

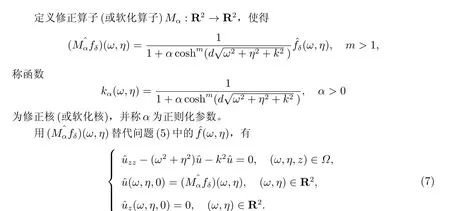
3 误差估计

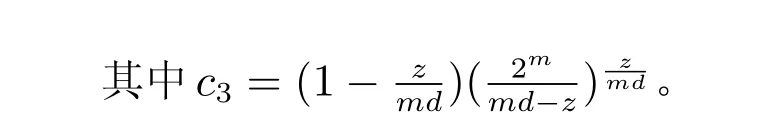
3.1 L2-估计

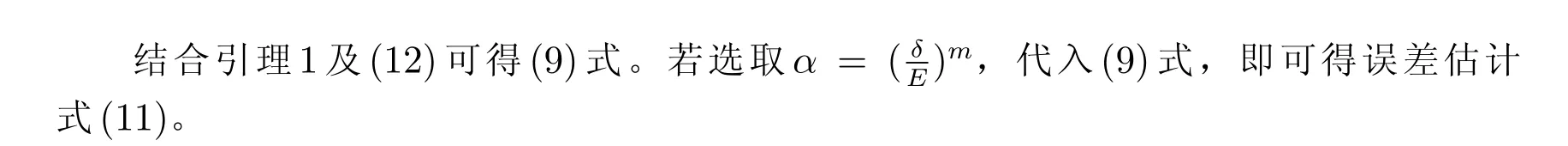
3.2 Hs-估计

引入比(2)、(3)式更强的先验界

4 数值实验

上节从理论上证明了修正核方法的收敛性和稳定性(在合适的正则参数选取下)。下面将用数值算例加以验证理论结果。所有计算在Matlab 2017b 中实现。数值例子中，考虑离散区间[-10,10]×[-10,10]，为了产生测量数据fδ(x,y)，方差为ϵ正态分布的随机扰动被加到数据f上，即

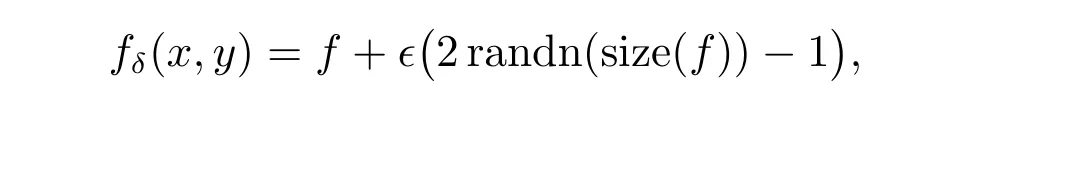
为了检验所给出算法的稳定性和有效性，检验了波数k，固定位置z以及噪音扰动δ取不同值时对应精确解与正则逼近解之间的相对误差。表1 和表2 分别列出了z=0.2 和z=0.8，波数k=0.5 与k=10 时，不同噪音扰动对应的正则解和精确解之间的相对误差。表3 和表4 列出了边界z= 1 处p分别取p= 3 和p= 12 对应波数k= 0.5, k=10 时不同δ对应的正则解和精确解之间的相对误差。

表1 z =0.2 时不同δ 和波数下的相对误差

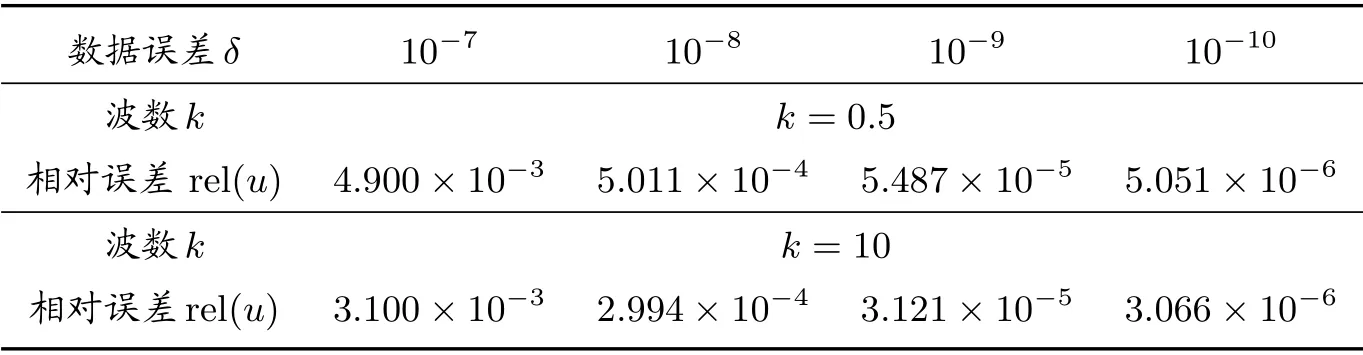
表2 z =0.8 时不同δ 和波数下的相对误差

表3 z =1, p=3 时不同δ 和波数下的相对误差

表4 z =1, p=12 时不同δ 和波数下的相对误差

图1 和图2 分别给出了在z= 0.3 处k= 1, δ= 10-4和k= 20, δ= 10-4的比较图。图3 展示了图1 和图2 对应下精确解与逼近解之间的误差。图4 和图5 分别展示了边界z= 1 处，δ= 10-10当k= 6, p= 3 和k= 6, p= 25 时精确解和逼近解比较图。图6 为图4 和图5 中精确解与近似解之间的误差。

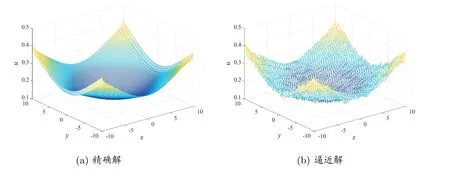
图1 当k =1, z =0.3, δ =10-4 时，对应的精确解和近似解

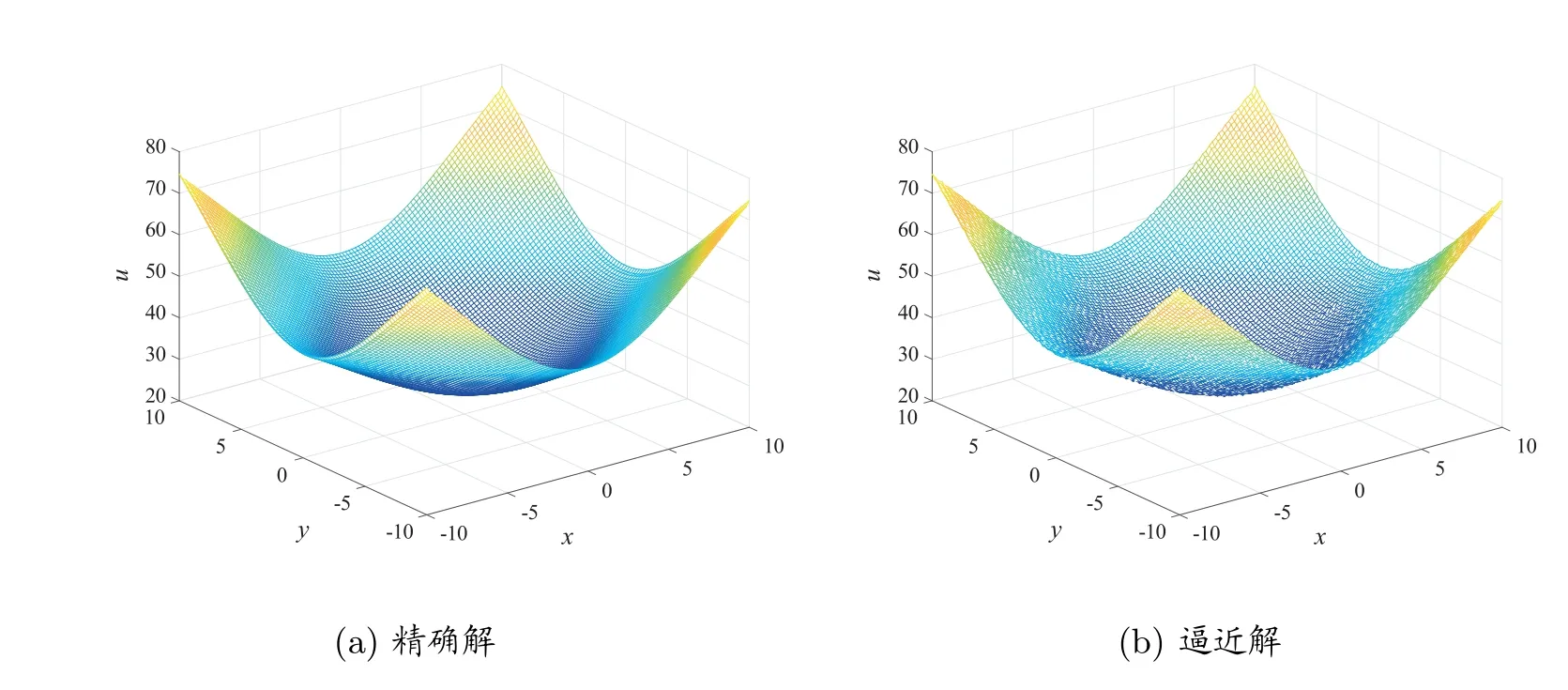
图2 当k =20, z =0.3, δ =10-4 时，对应的精确解和近似解

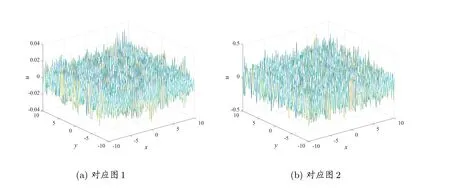
图3 精确解与逼近解之间的误差

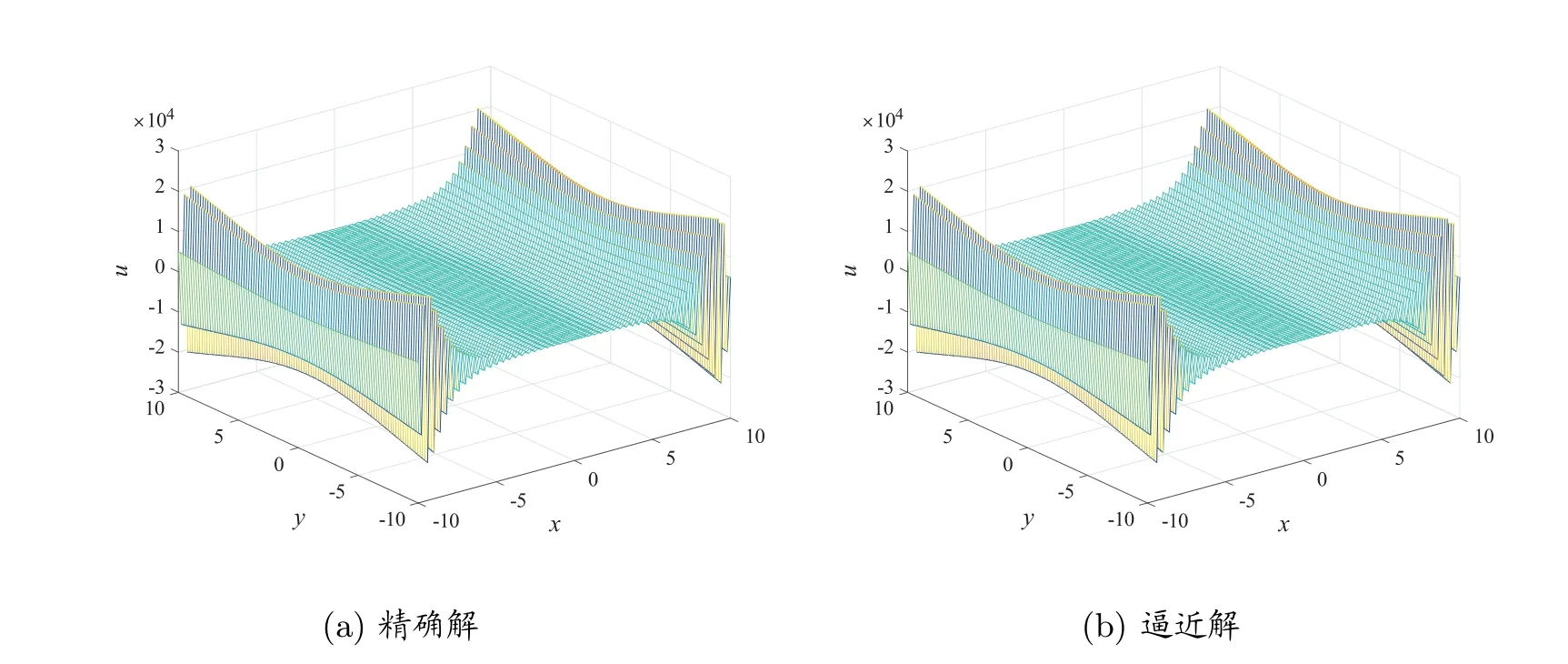
图4 当k =6, p=3, δ =10-10 时，边界z =1 处的精确解和逼近解

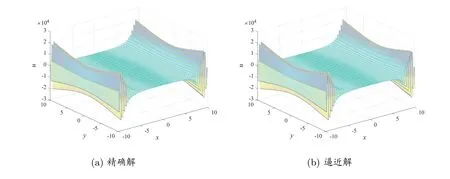
图5 当k =6, p=25, δ =10-10 时，边界z =1 处的精确解和逼近解

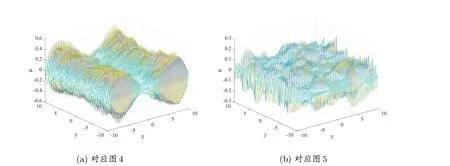
图6 边界z =1 处精确解与逼近解之间的误差

由表1 至表4 以及图1 至图6 可知，精确解与逼近解之间的逼近度，不仅与波数k有关还与噪音扰动δ有关。特别是边界处，由于先验界由Sobolev 范数决定，所以在边界处精确解与逼近解之间的逼近程度除了与波数k，噪音扰动δ有关，还与p有关。总体来说，δ越小，逼近效果越好。也就是说，随着δ的减小，数值解越来越稳定。因此，本文所采用的修正核方法对于处理Helmholtz 类方程柯西问题是非常有效并且稳定的。

5 结论

本文考虑修正的Helmholtz 方程的Cauchy 问题。通过将原有精确解的核进行修正，得到正则近似解，用其逼近原问题的精确解。采用先验选取规则计算正则参数，得到了正则近似解与精确解之间的L2-型和Hs-型误差估计。数值算例验证了所采用软化正则化方法的有效性和稳定性。关于三维Helmholtz 方程的Cauchy 问题，亦可用本文方法解决，我们将在另文中给出。