矩阵代数上保Jordan可逆性的线性映射

生玉秋，库俊华

(琼台师范学院 数理系,海口 571127)

首先交代本文用到的符号.用C表示复数域，用C*来表示C中所有非零元构成的集合.Mn(C)和Tn(C)分别表示复数域上所有n阶阵和n阶上三角阵构成的矩阵代数,GLn(C)表示由Mn(C)中所有可逆阵构成的集合.对方阵A来说trA表示A的迹,AT表示A的转置矩阵.用I表示单位矩阵,用Eij表示(i,j)元为1,其余元都为零的矩阵,I和Eij的型可由上下文得出.

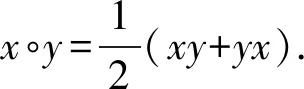
本文属于保持问题.保持问题由来已久，矩阵代数的保持问题文献很多,Peter Semrl和李志光分别在文献[1]和[2]中详细阐述了保持问题的常见类型及各种研究方法.随着保持问题研究的逐渐深入，其研究内容也从基础域和保持性质两方面逐渐拓展(参见文献[3-4]及其中的参考文献).例如保持性质方面从保持普通矩阵乘积的特殊性质拓展到保持矩阵Jordan乘积的相关性质(文献[5-8]).Louisa Catalano和Hayden Julius在文献[9]中刻画了满足如下条件的线性双射f:Mn(C)→Mn(C)，若XY=K,则f(X)f(Y)=M,其中K，M是Mn(C)中两个固定矩阵.Louisa Catalano等在文献[8]中研究了满足如下性质的线性双射φ:Mn(C)→Mn(C)，若X∘Y=K,则φ(X)∘φ(Y)=M,其中K，M是Mn(C)中两个固定矩阵.在此条件下，取K=M=I,若Y是X的一个Jordan逆，则φ(Y)是φ(X)的一个Jordan逆.Marcus和Purves在文献[10]中证明了Mn(C)上每一个保可逆的线性映射是一个内自同构或内反自同构.这个结果后来被推广到了其他代数上(参见文献[11-12]).本文研究矩阵代数的保Jordan可逆性的映射，即研究满足如下性质的线性映射φ:Λ→Λ，对每一个X∈Λ，存在矩阵Y∈Λ使得X∘Y=I当且仅当存在矩阵Z∈Λ使得φ(X)∘Z=I，其中Λ指M2(C)或T2(C).但若X∘Y=I，并不要求有φ(X)∘φ(Y)=I.高阶Jordan可逆矩阵的形式比较复杂，因此本文在二阶矩阵代数上考虑此类问题.

1 预备结果

引理1 1)设A为M2(C)中的一个非零阵，则A无Jordan逆的充要条件是秩A=1且trA≠0.

2)设A为T2(C)中的一个非零阵，则A在T2(C)中有Jordan逆的充要条件是A可逆.

证明1)显然，所有可逆阵都是Jordan可逆的.

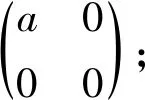
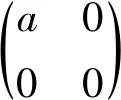
比较上式两端的(2,2)元可得0=2,矛盾.因此,A无Jordan逆的充要条件是秩A=1且trA≠0.

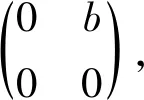
引理2 设f是M2(C)的一个保Jordan可逆性的线性映射,a∈C*,P∈GL2(C).令：

φ(A)=aP-1f(A)P,∀A∈M2(C)，

则φ也是M2(C)的一个保Jordan可逆性的线性变换.

2 主要结论

定理1 设f:M2(C)→M2(C)是一个保Jordan可逆性的线性映射,则存在a∈C*和P∈GL2(C)使得f(A)=aP-1AP或f(A)=aP-1ATP,∀A∈M2(C).

证明定理的充分性显然.下面证明定理的必要性.

由引理1知E11无Jordan逆,故f(E11)也无Jordan逆.若f(E11)为零矩阵，则由E11+E12无Jordan逆知f(E11+E12)=f(E11)+f(E12)=f(E12)也无Jordan逆，这与E12有Jordan逆矛盾，故f(E11)非零.再由引理1可知存在a∈C*和P∈GL2(C)使得f(E11)=aP-1E11P.由引理2,不失一般性，可记f(E11)=E11.

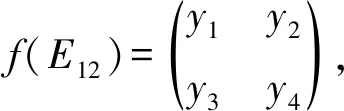
若f(E12)=cE12,f(E21)=d1E12,则f(E11+E12+E21)=aE11+(c+d1)E12，由引理1知f(E11+E12+E21)无Jordan逆，但E11+E12+E21可逆，从而有Jordan逆，矛盾.

类似地,f(E12)=dE21,f(E21)=c1E21亦可导出矛盾.于是以下可分两种情况讨论.

1)f(E12)=cE12,f(E21)=c1E21.

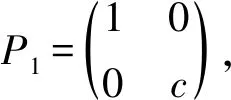
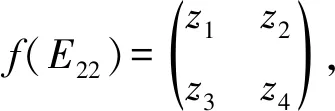
z1z4-z2z3=0,z1+z4≠0.

(1)

又由E12+E22,E21+E22都没有Jordan逆可知

均无Jordan逆.于是再由引理1知f(E12+E22)和f(E21+E22)均为秩1阵，故

z1z4-(z2+1)z3=z1z4-(z3+z)z2=0.

再结合式(1)可得z2=z3=0,z1z4=0,即f(E22)=z1E11或f(E22)=z4E22,z1,z4∈C*.

若f(E22)=z1E11,则f(E11+E22)=(1+z1)E11.由引理1知f(E11+E22)无Jordan逆，但E11+E22可逆，有Jordan逆，矛盾.因此f(E22)=z4E22.

2)f(E12)=dE21,f(E21)=d1E12.

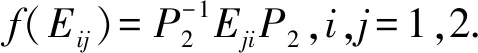
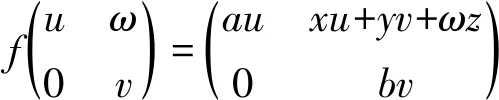
证明类似定理1的证明可知f(E11)和f(E22)均非零.

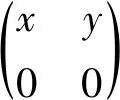
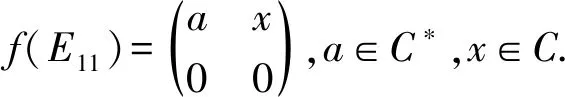
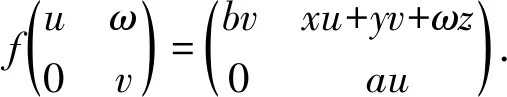
3 结语

高阶的Jordan可逆矩阵的形式比较复杂多样，这就导致高阶矩阵代数上此类问题的解决难度大增.高阶矩阵代数的保Jordan可逆性的线性映射的刻画仍是有待解决的公开问题.