巧借整体思想 解答数学难题

黄美金

(福建省闽侯县第一中学 350199)

整体思想指考虑问题时将某些图形、式子作为一个整体进行考虑的思想.高中数学知识点多，习题灵活多变，尤其部分习题难度较大，采用常规思路求解的难度较大，在整体思想指引下往往能够迅速的找到解题思路，因此为启发学生在解题中更好的应用整体思想，应将整体思想的应用渗透至习题教学中.

一、借助整体思想，解答对数难题

对数难题中的“难”主要体现在两个方面：其一，涉及有关对数的运算灵活性较大；其二，将对数知识和其他知识结合起来出题，综合性较强.解答对数难度时应结合题干中的已知条件，积极回顾所学，在整体思想的指引下灵活运用对数的运算法则，进行巧妙的变形与转化，进行严谨的推理.

已知函数f(x)=ax3+bsinx+4(a，b∈R)，f[lg(log210)]=5，则f[lg(lg2)]的值为( ).

A.1 B.2 C.3 D.4

该题目题干简洁，较为抽象，如掌握不住技巧难以作答.解答该题需充分挖掘函数表达式，从中找到隐含条件，而后运用整体思想进行巧妙作答.

∵f(x)=ax3+bsinx+4…①，∴f(-x)=-ax3-bsinx+4…②，①+②得：f(x)+f(-x)=8…③

二、借助整体思想，解答不等式难题

不等式是高中数学的重要知识点，解题思路灵活多变，尤其当题目中涉及到导数知识时，常需要学生构造新的函数，运用整体思想加以突破.解答不等式难题的关键在于能够深入理解已知条件，准确的把握要求解问题的特征，构造出合理的函数，运用函数的单调性顺利解答.

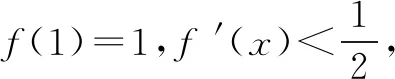
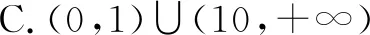
题目融合了复合函数、导数知识，具有一定的技巧性.遇到复合函数可考虑整体思想，进行换元以简化解题难度.

三、借助整体思想，解答最值难题

最值问题在高中数学中较为常见，求解的思路主要有：运用函数性质、运用均值不等式知识.其中针对部分习题，看似无法直接应用均值不等式知识，但只要利用整体思想进行巧妙的化解，凑出能够运用均值不等式的形式，问题也就迎刃而解.

解答该题需要认真分析已知条件与要求解分式之间的内在联系，经过巧妙的处理运用整体思想进行解答.因该题中含有两个变量，因此可采用双换元法对要求解的问题进行转化，对要求解的式子重新构造.

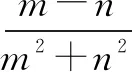
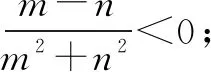
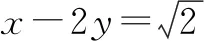
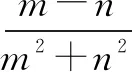
四、借助整体思想，解答三角函数难题

三角函数是高考中的必考知识点.为使学生更好的掌握相关难题的解题思路，体会整体思想在三角函数难题中的具体应用，应结合学生的做题反馈，筛选与讲解代表性较强的习题，给学生带来良好的解题启发，更好的把握整体思想的应用细节.

A.0 B.2 C.0或2 D.0或1

题目中的已知条件只是一个等式，要求解的是分式的值，如思路不正确难以作答.授课中可给予学生针对性的指引，启发其采用整体思想通过换元构建已知条件和要求解问题之间的关系.同时，注重联系、运用三角函数中的隐含条件，构建对应的等式关系，以顺利的求解出最终结果.

高中数学教学中为使学生能够灵活应用整体思想解答相关难题，课堂上应以具体的例题为代表，与学生一起分析习题难在何处、考查了哪些知识点、是如何进行破题的，应用整体思想注意哪些细节等.同时，鼓励学生做好听课总结，分析从习题的解答中获得了哪些启发，暴露出解题中的哪些不足，结合自身实际加以针对性的学习与弥补，真正的掌握整体思想在解题中的妙用.