晒晒集合中常用的数学思想
杜红全
(甘肃省康县教育局教研室 746500 )
数学思想是数学知识的精髓,既是知识转化为能力的桥梁,又是解数学问题寻找思路的依据,它蕴含在高中数学的各个章节中.下面举例说明集合中常用的数学思想,供参考.
一、数形结合思想
数形结合,由数思形,由形定数,起到互补、互动、互译作用,可见数形结合的思想可以使某些抽象的数学问题直观化、生动化,能够变抽象思维为形象思维,有助于把握数学问题的本质.使用数形结合思想可以使问题化难为易,化抽象为具体.运用数形结合思想解题通常有三种类型:由形化数,由数化形,数形转化.
例1 已知集合A={x|1≤x<4},B={x|x 分析把集合在数轴上表示出来,借助数轴直接求解. 解将集合A表示在数轴上,如图1所示,要满足AB,表示数a的点必须在表示4的点处或在表示4的点的右边,所以所求实数a的取值范围是{a|a≥4}. 点评求解这类问题的关键是要利用数轴,数形结合;将集合A表示在数轴上,由数化形,求实数a的取值范围是由形化数,同时要注意验证端点值,做到准确无误;解决有关交集、并集问题,特别是求一些字母取值范围的问题常用数形结合思想方法. 所谓分类讨论,就是当问题所给对象不能进行统一研究时,我们就需要对研究的对象进行分类,然后对每一类分别研究,得出每一类的结论,最后综合各类的结果得到整个问题的解答.分类讨论实质上就是“化整为零,各个击破,再积零为整”的策略. 例2 设集合A={x|x2+2x=0},B={x|x2+2ax+a2-a=0,a∈R,x∈R},若B⊆A,求实数a的取值范围. 分析由于B⊆A,所以集合B可以为空集,可以B与A相等,也可以B为A的非空真子集,需分三种情况进行讨论. 解因为A={x|x2+2x=0}={-2,0},B⊆A,所以有B=φ、B=A或BA(B≠φ). (1)当B=φ时,Δ=4a2-4(a2-a)<0,解得a<0; (3)当BA(B≠φ)时,有B={-2}或B={0},所以Δ=4a2-4(a2-a)=0,解得a=0,此时B={x|x2=0}={0}满足条件. 综上可知,实数a的取值范围为a≤0或a=1. 点评解答本题的关键是理解好子集的含义;B⊆A可分B=φ、B=A或BA(B≠φ)三种情况,所以此类问题需要分类,并结合一元二次方程根的情况加以解决;分类时要遵循“确定对象的全体,明确分类标准,做到不重不漏”的原则,然后对于每一类情况都要给出问题的解答. 方程思想就是从分析问题的数量关系入手,把变量之间的关系用方程的关系来反映,然后通过解方程或对方程进行讨论的数学方法. 分析利用集合相等,它们所含的元素相同,列方程来确定a,b的值,再求a2021+b2021的值. 点评求解本题的关键是利用集合相等的概念,借助相等的关系列方程求出字母的值,但要注意排除与集合元素互异性或已知相矛盾的情况. 有些数学问题,若直接从正面解决比较困难,或考虑的因素比较多,可以考虑求问题的反面,采用间接的方法将问题解决,这就是正难则反思想.在解决“至多”、“至少”等一类问题时,常用这种思想方法,在集合中正难则反思想就是补集思想. 例4 已知集合P={x|4 分析P∩Q≠Q直接考虑情况很多,非常麻烦,因此考虑它的反面,即P∩Q=Q,求出答案,只要求它的补集即可. 综上所述,当P∩Q=Q时,k的取值范围是{k|k≤2,或3 点评求解本题的关键是将求P∩Q≠Q时的k的取值范围转化为求其对立面P∩Q=Q时的k的取值范围,再取补集得出原问题的解;正难则反思想作为一种思想方法,为我们研究问题提供了新思路,在正向思维受阻的情况下,改用逆向思维,可能“柳暗花明”,从这个意义上讲,正难则反思想具有转换研究对象的功能. 所谓转化思想方法,就是在研究和解决有关数学问题时,采用某种手段将问题通过变换使之转化,从而达到解决问题的一种方法.转化思想方法可以将难解的、复杂的、未解决的问题通过变换转化为较容易的、简单的、已解决的问题. 例5 已知集合M={(x,y)|y=x-2,x∈R},N={(x,y)|y=ax2-ax+a,x∈R},问是否存在非零整数a,使得M∩N≠φ. 点评求解本题的关键将待求问题转化为讨论方程组是否有解的问题,从而顺利获解.
二、分类讨论思想
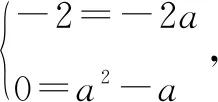
三、方程思想
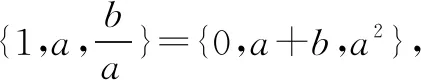
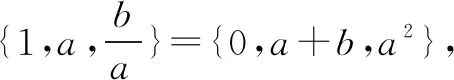
四、正难则反思想
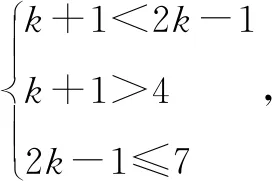
五、转化思想



