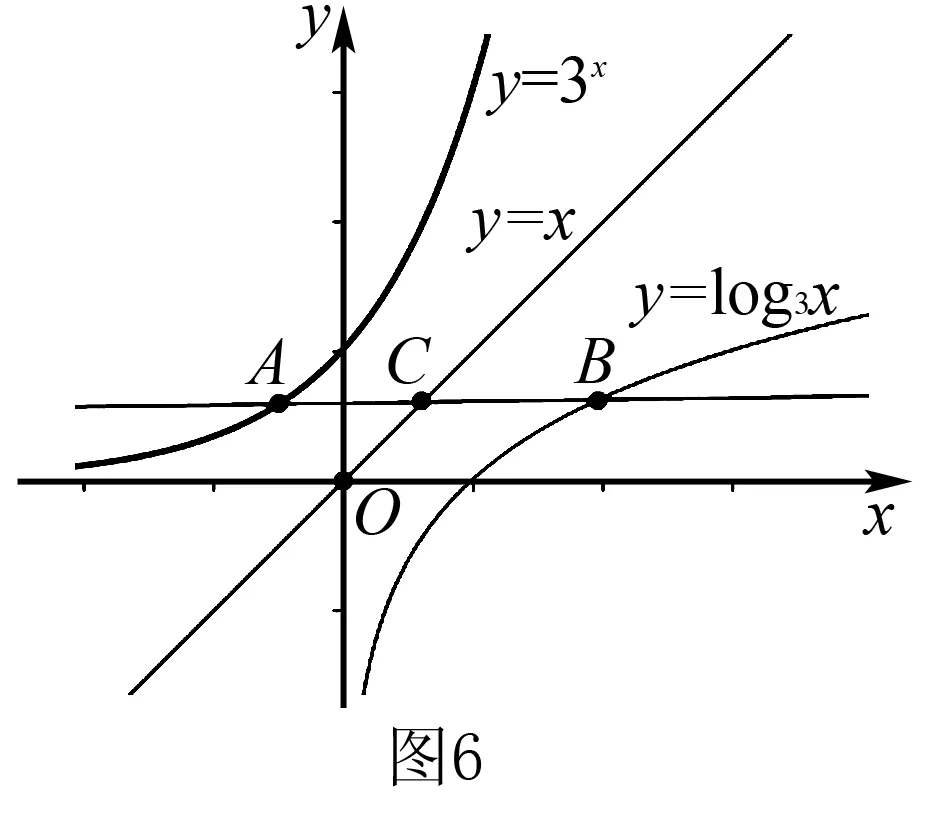
两个指数型函数在解题中的应用举例
苏艺伟
(福建省龙海第一中学新校区 363100)
函数y=ax+a-x(a>0且a≠1)以及y=ax-a-x经常出现在高三年级的模拟试题当中,掌握好这两个函数的相关图像,性质能够帮助我们更好地解决数学问题.
一、知识链接
1.y=ax+a-x(a>0且a≠1)
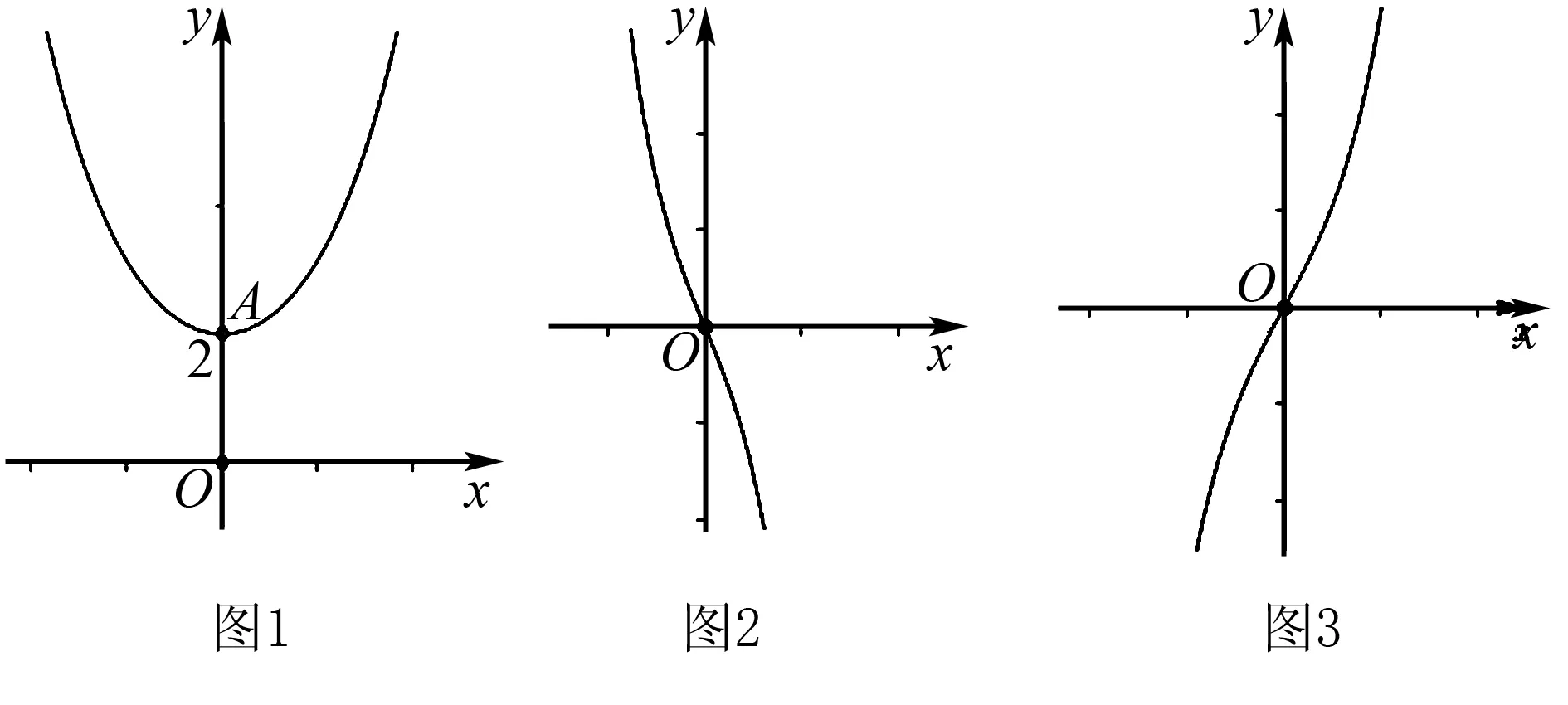
函数y=ax+a-x(a>0且a≠1)图象如图1所示,该函数是一个偶函数,最小值为2,在(-∞,0)单调递减,在(0,+∞)单调递增.
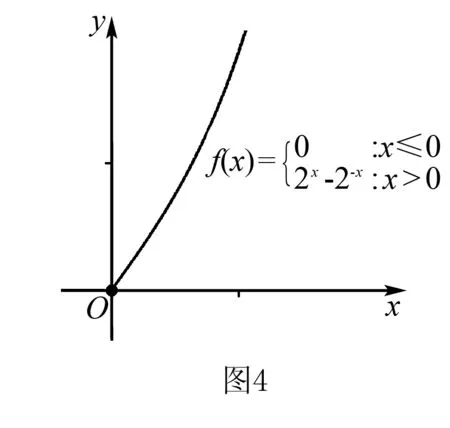
2.y=ax-a-x(0 函数y=ax-a-x(0 3.y=ax-a-x(a>1) 函数y=ax-a-x(a>1)图象如图3所示,该函数是一个奇函数,图像经过点(0,0),在R单调递增. 对于上述函数模型,最经常出现的是a=2,a=e的情形,有些时候还会出现由上述函数模型经过左右平移而得到的新函数.在实际解题中,应该抓住这三个基本的函数模型,以不变应万变,灵活应用,正确解答. 例1下列函数中,图像关于原点对称且单调递增的是( ). A.f(x)=sinx-xB.f(x)=ln(x-1)-ln(x+1) A.(-∞,-1)∪(2,+∞) 例3已知函数f(x)=x2(2x-2-x),则不等式f(2x+1)+f(1)≥0的解集是( ). 解析易知f(-x)=-f(x),所以f(x)为奇函数.又f′(x)=2x·(2x-2-x)+x2(2x+2-x),当x>0时,f′(x)>0,因此f(x)在(0,+∞)上单调递增.由于f(x)为奇函数,所以f(x)在R上单调递增.f(2x+1)+f(1)≥0⟺f(2x+1)≥-f(1)⟺f(2x+1)≥f(-1)⟺2x+1≥-1⟺x≥-1.故不等式f(2x+1)+f(1)≥0的解集是{x|x≥-1}. 图5 例5已知函数f(x)=ex-e-x-2x, (1)讨论f(x)的单调性; (2)设g(x)=f(2x)-4bf(x),当x>0时,g(x)>0,求b的最大值. 解析(1)f′(x)=ex+e-x-2≥0,f(x)在R上单调递增. (2)g(x)=e2x-e-2x-4x-4bex+4be-x+8bx g′(x)=2(ex+e-x-2)(ex+e-x-2b+2) 令h(x)=ex+e-x-(2b-2) 若2b-2≤2,即b≤2时,h(x)>0,g′(x)>0,g(x)在(0,+∞)上单调递增,g(x)>g(0)=0,符合题意. 综上有b≤2,因此b的最大值为2. 例6已知函数f(x)=x2-2x+a(ex-1+e-x+1)有唯一零点,求a的值. 例7已知函数f(x)=ex-a+e-x+a,若3a=log3b=c,则( ). A.f(a) C.f(a) 解析由于f(2a-x)=e-x+a+ex-a,因此f(2a-x)=f(x),所以f(x)的图像关于直线x=a对称且f(x)在(a,+∞)上单调递增.由图6可知,a 因此f(a) 例8设f(x)=-x2+2x-2(ex-1+e1-x),则使得f(x+1) 解析由于f(2-x)=f(x),故f(x)图像关于直线x=1对称,因此f(x+1)图像关于直线x=0对称.令g(x)=f(x+1)=-x2+1-2(ex+e-x),则g(x)为偶函数且在(0,+∞)上单调递减. f(x+1) 例9已知函数f(x)=emx+e-mx+x2-mx的图象在点A(x1,f(x1)),B(-x1,f(-x1))处两条切线的交点P(x0,y0)一定满足( ). A.x0=0 B.x0=mC.y0=0 D.y0=m 解析由f(x)=emx+e-mx+x2-mx得f′(x)=memx-me-mx+2x-m.点A(x1,f(x1))处的切线方程为y-f(x1)=f′(x1)(x-x1);点B(-x1,f(-x1))处的切线方程为y-f(-x1)=f′(-x1)(x+x1);又点P(x0,y0)满足以上两式,所以y0-f(x1)=f′(x1)(x0-x1),y0-f(-x1)=f′(-x1)(x0+x1);两式相减得f(-x1)-f(x1)=x0[(f′(x1)-f′(-x1))]-x1[(f′(x1)+f′(-x1))],又f(-x)-f(x)=2mx,f′(x)+f′(-x)=-2m,所以2mx1=x0[(f′(x1)-f′(-x1))]+2mx1,故x0=0. 不难发现,以函数y=ax+a-x(a>0且a≠1)和y=ax-a-x为载体的试题,常融入函数的对称性,单调性,零点,最值等于一体,结合图像,不等式,导数等重要知识点,体现了高考评价体系提出的基础性,综合性,应用性,创新性的要求.试题虽然简短但却闪耀着智慧的光芒.在实际解题中,要抓住这两个最基本的模型,由它们出发引申出一系列的变式,进而掌握好此类题型. 练习1已知函数f(x)=x2-4x+(m2-m)(ex-2+e-x+2)有唯一零点,则m的值可以是____. 解析由于y=x2-4x和y=ex-2+e-x+2对称轴都是x=2,所以f(x)的对称轴是x=2.故令f(2)=0得m=2或m=-1. 练习2已知f(x)=ex-1-e1-x+x,则不等式f(x)+f(3-2x)≤2的解集是____. 解析由于f(x)+f(2-x)=2,所以不等式f(x)+f(3-2x)≤2,即为f(x)+f(3-2x)≤f(x)+f(2-x),即f(3-2x)≤f(2-x),又f′(x)>0,f(x)单调递增,所以3-2x≤2-x,x≥1.故解集为{x|x≥1}. 练习3已知函数f(x)=x2-4x-1+ex-2+e-x+2有两个零点,则x1+x2=____.二、基础应用
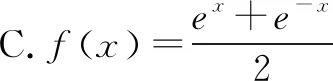
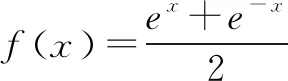
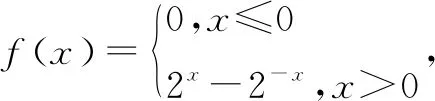
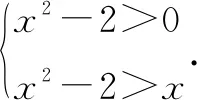
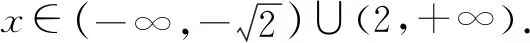
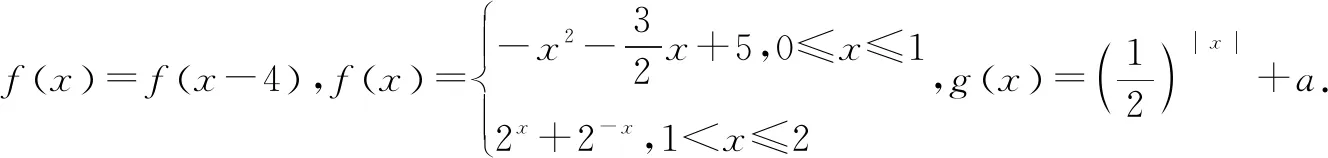
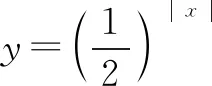
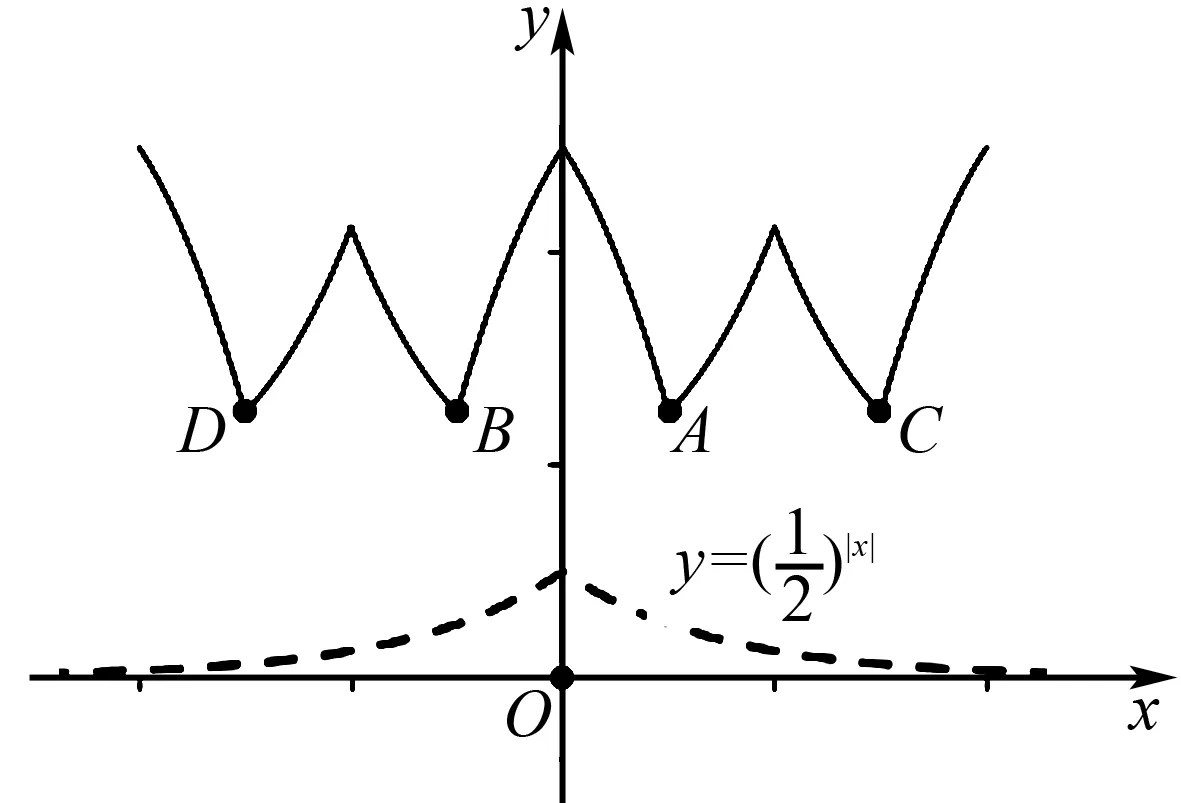
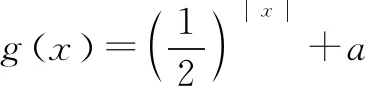
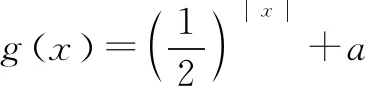
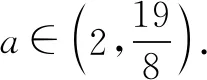

三、拓展应用