基于周期性扰动学习的永磁直线电机自适应滑模位置控制

张康，王丽梅

(沈阳工业大学 电气工程学院，沈阳 110870)

0 引 言

永磁直线同步电机(permanent magnet linear synchronous motor，PMLSM)与旋转同步电机相比，具有更高的推力密度，更低的热损耗，而且不存在机械耦合和滚珠丝杠问题，因此，广泛应用于数控加工系统[1]。由于采用直接驱动方式，PMLSM伺服系统对系统周期性扰动、参数摄动及负载扰动等因素变得更加敏感，影响系统位置控制精确度。所以采取有效的控制策略抑制系统扰动，提高PMLSM的位置跟踪性能对提高机床加工精确度具有重要的意义。

针对PMLSM伺服系统的高精密控制问题，文献[2]采用电流预测控制策略，通过提高PMLSM的电流环特性，来提高系统的跟踪特性，但需要被控对象的精确数学模型。文献[3]针对PMLSM驱动系统中存在的干扰，设计了速度前馈控制器、零相位误差跟踪控制器和扰动观测器，实验结果表明了其控制策略的有效性，但扰动观测器不能很好地解决系统抗干扰性能与鲁棒稳定性之间的矛盾。滑模控制(sliding mode control，SMC)是一种常用的非线性控制方法，具有响应快、鲁棒性强、实现简单等优点[4]。但传统滑模控制中，为了保证系统具有较强的鲁棒性和稳定性，切换增益的设置要足够大，以抵消系统的扰动，但较大的切换增益会导致高频滑模抖振的发生[5]。文献[6]采用 Elman神经网络估计PMLSM伺服系统扰动，替代滑模控制律中的切换项，削弱了抖振现象，但系统的鲁棒性也随之降低。文献[7]针对PMLSM系统利用小波神经网络和粒子群算法结合观测系统的不确定性，明显地削弱了滑模抖振现象，但算法较为复杂，降低了系统响应速度。文献[8]设计自适应律估计PMLSM伺服系统扰动的上界，改善滑模的抖振现象，由于把系统所有扰动进行集总估计，导致估计误差较大，改善效果并不理想。

迭代学习控制(iterative learning control，ILC)可以利用之前的信息改善当前的控制输入信号，提高系统的位置跟踪性能，因此在PMLSM系统控制领域得到了广泛研究[9-10]。文献[11]将分段变论域模糊ILC应用到PMLSM系统中，使系统根据实际输出误差在变论域模糊ILC和PD型ILC之间实时切换，保证系统实现了高精确度的位移跟踪和鲁棒性，但是该方法对非周期性扰动非常敏感，容易导致跟踪精确度降低，甚至系统发散。文献[12]将小波滤波器应用到ILC算法中，利用小波滤波器剔除误差的非周期分量，重构输入误差信号，加快了系统的收敛速度，但误差信号失真对系统的控制性能可能产生影响。

针对PMLSM伺服系统存在的周期性扰动、参数摄动及负载扰动等不确定性，提出了一种自适应滑模控制(adaptive sliding mode control，ASMC)和周期性扰动学习(periodic disturbance learning，PDL)算法相结合的控制策略。滑模控制保证系统对不确定性扰动具有较强的鲁棒性能。将系统扰动分为周期性扰动和非周期性扰动，利用ILC的学习能力设计PDL算法，对周期性扰动进行学习和补偿，削弱系统抖振。同时设计自适应律估计非周期性扰动和学习误差，进一步改善控制性能。最后对所提出的控制方法的有效性进行实验验证。

1 PMLSM的数学模型

忽略磁通畸变，d-q轴模型电压方程为:

vd=Rsid+pλd-πvλq/τ，

(1)

vq=Rsiq+pλq+πvλd/τ。

(2)

式中：Rs为相电阻；vd、vq为d-q轴电压；id、iq为d-q轴电流；λd、λq为d-q轴磁链；λd=Ldid+λPM；λq=Lqiq；Ld、Lq为d-q轴电感；λPM为励磁磁链；τ为极距；v为动子线速度；p为微分算子。

理想情况下，PMLSM的电磁推力为

(3)

基于id=0磁场定向控制，电磁推力表示为

(4)

式中Kf为推力系数。

PMLSM运动方程为

(5)

式中：M为动子及所带负载的总质量；x为动子位置；B为粘滞摩擦系数；Ffriction为摩擦力；Fripple为推力波动；Fd为负载扰动主要包括系统模型不确定性、电机动子质量变化及测量扰动等非线性因素引起的随机扰动。

摩擦力用LuGre模型[13]表示为

Ffriction(v)=FCsgn(v)+(FS-FC)e-(v/vs)2sgn(v)。

(6)

式中：sgn(·)为符号函数；FC和FS分别为库仑摩擦系数和静摩擦系数；v为动子速度；vs为临界Stribeck速度。

由端部效应引起的以动子位置信号x为自变量的周期性扰动的基波模型[13]可以表示为

Fripple(x)=Fripmcos(2πx/τ+φ0)。

(7)

式中：Fripm是端部效应力的幅值；τ为极距；φ0为初始相位电角度。

存在扰动情况下，直线电机动子位置x和电磁推力Fe之间的传递函数为

(8)

2 PDL-ASMC位置控制器设计

2.1 永磁直线电机伺服系统组成

伺服系统的控制目标就是在系统受周期性推力波动、摩擦力及参数摄动等不确定性受影响时所设计的控制器，使系统输出可以跟踪任意给定输入。永磁直线伺服控制系统框图如图1所示。在系统中控制器包括PI电流控制器和PDL-ASMC位置控制器。利用PDL算法对系统中的周期性扰动进行学习并补偿；滑模控制提高系统的鲁棒性；采用自适应控制估计系统非周期性扰动和学习误差，削弱系统抖振。

图1 永磁直线电机伺服控制系统Fig.1 Permanent magnet linear motor servocontrol system

2.2 PDL-ASMC控制器设计

为方便控制器设计，将PMLSM动力学系统重新描述如下，其中扰动分为周期性扰动和非周期性扰动

(9)

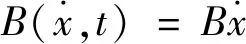
为保证严密性，假设满足下面的条件：

假设1 期望轨迹xd(t)在迭代周期[0,T]内，对于时间t是二阶可微的。

假设2 非周期性扰动r(t)有界

|r(t)|≤rd,∀t∈[0,T]。

(10)

e(t)=xd(t)-x(t)。

(11)

对于PMLSM系统，采用跟踪误差及其时间导数的线性组合来定义滑模面

(12)

式中：c必须满足Hurwitz条件，即c>0。

对式(12)两边同时对时间t求导得

(13)

将式(9)代入式(13)可得滑模面S(t)的动态方程为

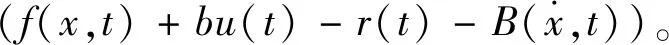
(14)

当S(t)=0时，系统状态轨迹到达滑模面。

在第k次学习的PDL-SMC位置控制器设计为

(15)

PDL控制器设计为

(16)

式中：q、β1、β2为正常数；Sk(t)为第k次学习时的滑模面。

设计滑模控制律为

vk(t)=-gsgn(Sk)-ηSk(t)。

(17)

式中g>0为切换增益；sgn(S)为开关函数可以表示为

(18)

将式(15)代入式(14)，滑模面动态方程可以简化为

(19)

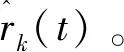
在第k次学习的PDL-ASMC位置控制器设计为

(20)

自适应律设计为

(21)

式中γ为正常数。估计误差定义为

(22)

将式(20)代入式(14)得

(23)

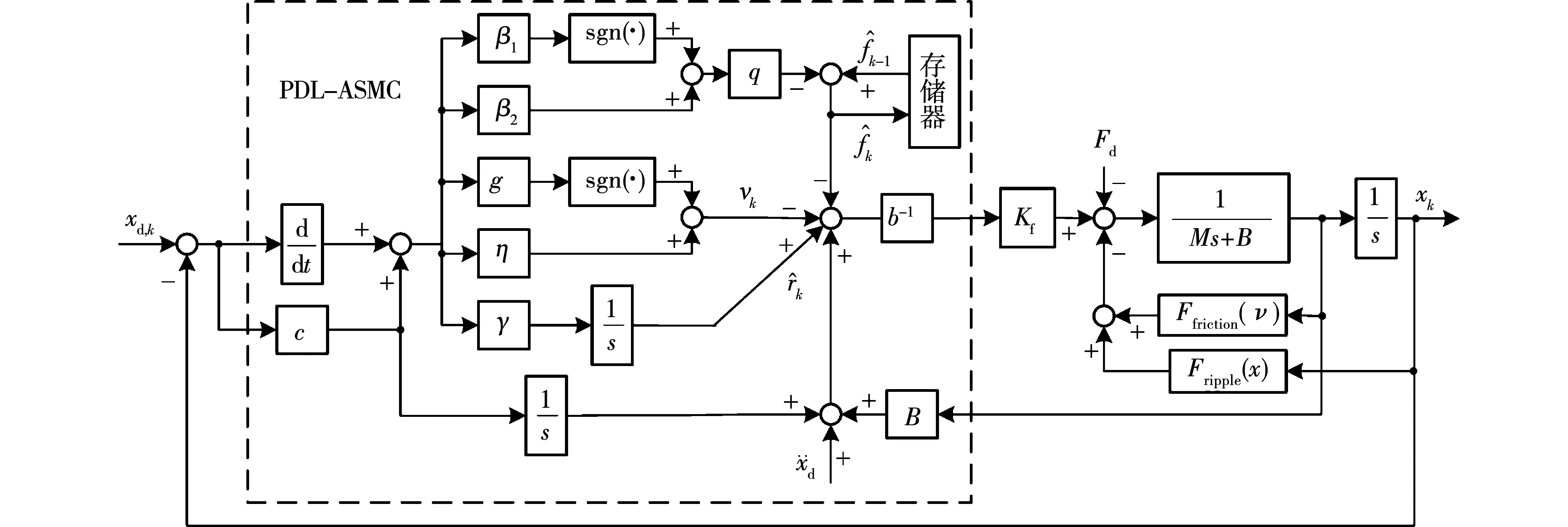
图2 基于PDL-ASMC控制器的 PMLSM 伺服控制系统框图Fig.2 Block diagram of PMLSM servo control system based on PDL-ASMC controller

2.3 稳定性分析

定理1 对于PMLSM系统，在假设1到3的条件下，当迭代次数接近无穷大时，式(20)中提出的控制律可以保证直线电机伺服系统位置跟踪误差在[0,T]上渐近收敛于零。

证明：为了证明位置跟踪误差e(t)和滑模面S(t)的收敛性，在第k次学习中定义李雅普诺夫函数为

(24)

证明包括两个步骤。第一步是推导两个连续迭代之间Lyapunov函数Vk(t)的差值。同时，第二步是对位置跟踪误差的收敛性进行证明。

1)连续两次学习Lyapunov函数的差值。

(25)

(26)

根据式(25)和式(26)，可得

(27)

将式(23)代入上式，并考虑式(17)，可得

(28)

考虑到sgn(Sk)Sk=|Sk|，可将上式简化为

(29)

(30)

对β1|Sk(t)|求导，可得

(31)

根据式(30)和式(31)，可得

(32)

将式(23)和式(17)代入上式，可得

β1|Sk-1(t)|。

(33)

(34)

由经验方程(a-b)T(a-b)-(a-c)T(a-c)=(c-b)T(2(a-b)+(b-c))可得

(35)

根据式(16)，可将上述方程展开为

(36)

(37)

(38)

(39)

根据式(38)和式(39)，可得

(40)

(41)

2)位置跟踪误差的收敛性

结合式(29)、式(33)、式(37)和式(41)，可以得到李雅普诺夫函数Vk(t)在第k次学习和第k-1次学习之间的差值为

(42)

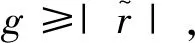
ΔVk(t)≤0。

(43)

基于李雅普诺夫稳定性理论,当Sk(t)≠0，t∈[0,T] 时，V(t)是负定的，表明李雅普诺夫函数V(t)是收敛的，可以确保系统状态在有限时间内到达滑模面。另外，由于滑模面的定义满足Hurwitz多项式，所以位置跟踪误差e(t)是渐近收敛的。

3 仿真结果与分析

系统仿真实验中永磁直线同步电机参数：M=0.38 kg,τ=14 mm,B=0.8 N·s/m,Rs=1.1 Ω,Kf=28.5 N/A,Ld=Lq=0.019 H,λPM=0.028 Wb。周期性扰动参数FC=10 N,FS=20 N,vs=0.5(LuGre型摩擦力)；Fripm=30 N，φ0=0 (端部效应)。分别采用带饱和函数的滑模控制器(S-SMC)和PDL-ASMC位置控制器进行控制，并比较仿真结果。S-SMC位置控制律为

(44)

式中：Φ为边界层厚度；sat(·)为饱和函数。

S-SMC位置控制器参数设置为：c=50；β1=2.1；Φ=0.001，PDL-ASMC位置控制器参数设置为：c=50；β1=0.4；β2=0.3；g=0.6；η=160；γ=0.003；q=0.1。

期望位置输入曲线如图3所示，稳态后在3.4 s时加入50 N负载阻力。在PDL逼近周期性扰动的过程中，各次学习误差的均方均根如图4所示。由图4可以看出，随着学习次数的增加，学习误差的均方根渐进收敛。图5、图6分别为学习15次后的学习结果和学习误差，可以看出PDL可以精确地学习系统的周期性扰动。

图3 正弦期望位置输入Fig.3 Sinusoidal expected position input

图4 学习误差均方根Fig.4 Root mean square of learning error

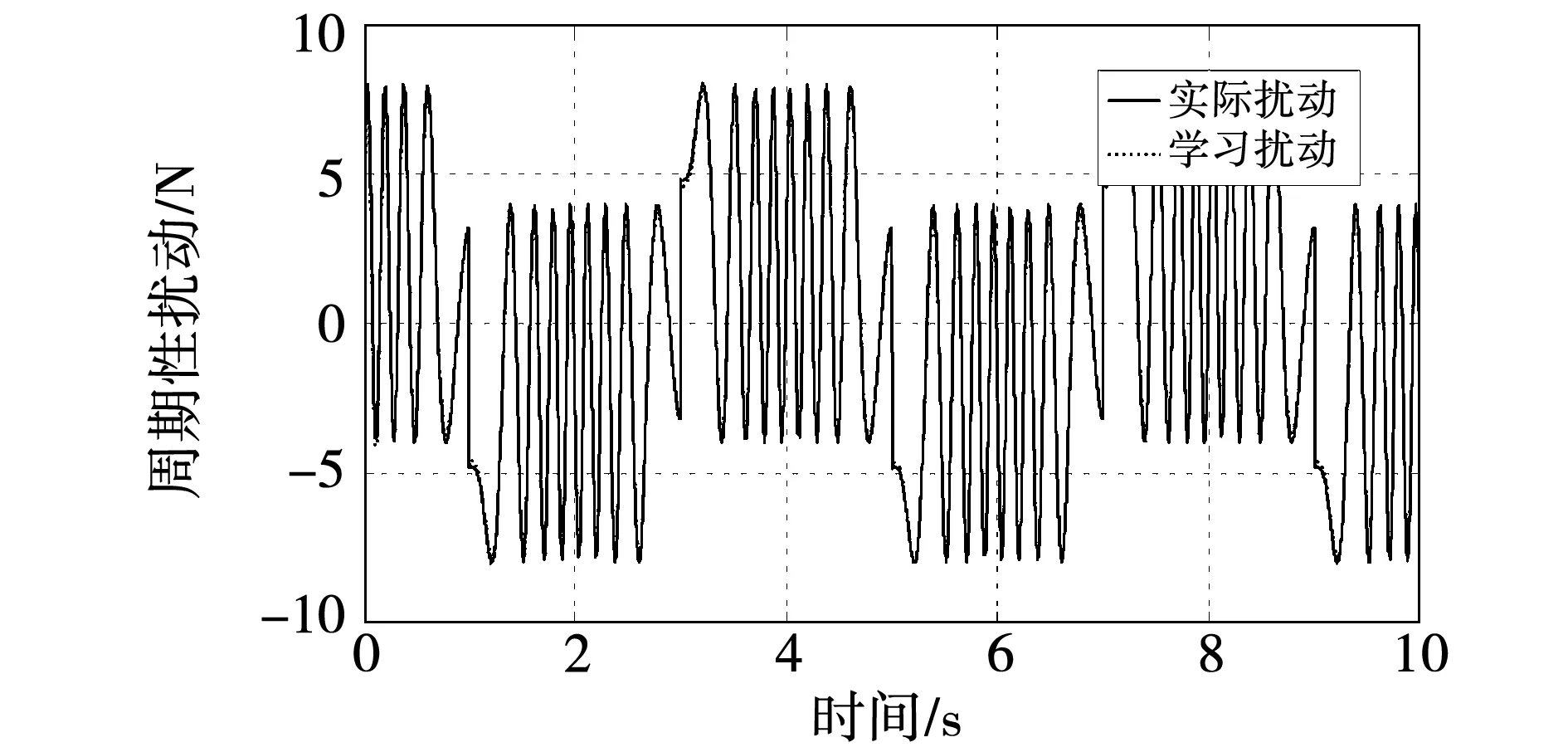
图5 扰动学习值与实际扰动Fig.5 Disturbance learning value and actual disturbance

图6 第15次迭代的学习误差Fig.6 Learning error of the 15th iteration

图7(a)和图7(b)分别为S-SMC控制和学习15次之后的PDL-ASMC位置跟踪误差曲线。图7(a)可以看出ASMC控制的位置稳态误差控制在±6.76 μm之间，由图7(b)可以看出PDL-ASMC的位置稳态误差控制在±1.0 μm之间。在3.4 s突加负载后，S-SMC控制的位置误差波动为2.41 μm，稳态恢复时间为 0.27 s ，而PDL-ASMC的位置误差波动为0.39 μm，稳态恢复时间为 0.12 s。因此可看出，当系统受周期性扰动和突加负载的非周期性扰动时，PDL-ASMC系统由于利用PDL学习周期性扰动的结果对系统进行补偿以及采用自适应律对学习误差和非周期性扰动进行估计，使得其稳态误差更小，稳态恢复时间更快，鲁棒性更强。

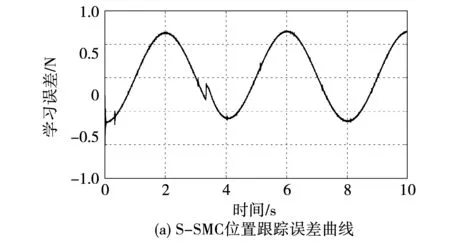
图7 输入正弦信号时系统位置跟踪误差曲线Fig.7 Position tracking error curve of system when inputting sinusoidal signal

4 实验结果与分析

基于数字信号处理器的PMLSM伺服系统实验硬件结构图如图8所示。实验选用TMS320F28335作为核心控制单元，采样周期为0.5 ms，伺服系统主要由永磁直线同步电机、PC+DSP运算控制单元、固定分辨率为0.05 μm的直线光栅尺，霍尔电流传感器，IPM逆变器。利用汇编语言实现控制算法及电流矢量控制，输出6路PWM波控制IPM 模块的导通。图9为基于DSP的PMLSM实验系统实物图，实验数据通过485串口传送给上位机。在实验中，电机参数和控制器参数与仿真实验相同。

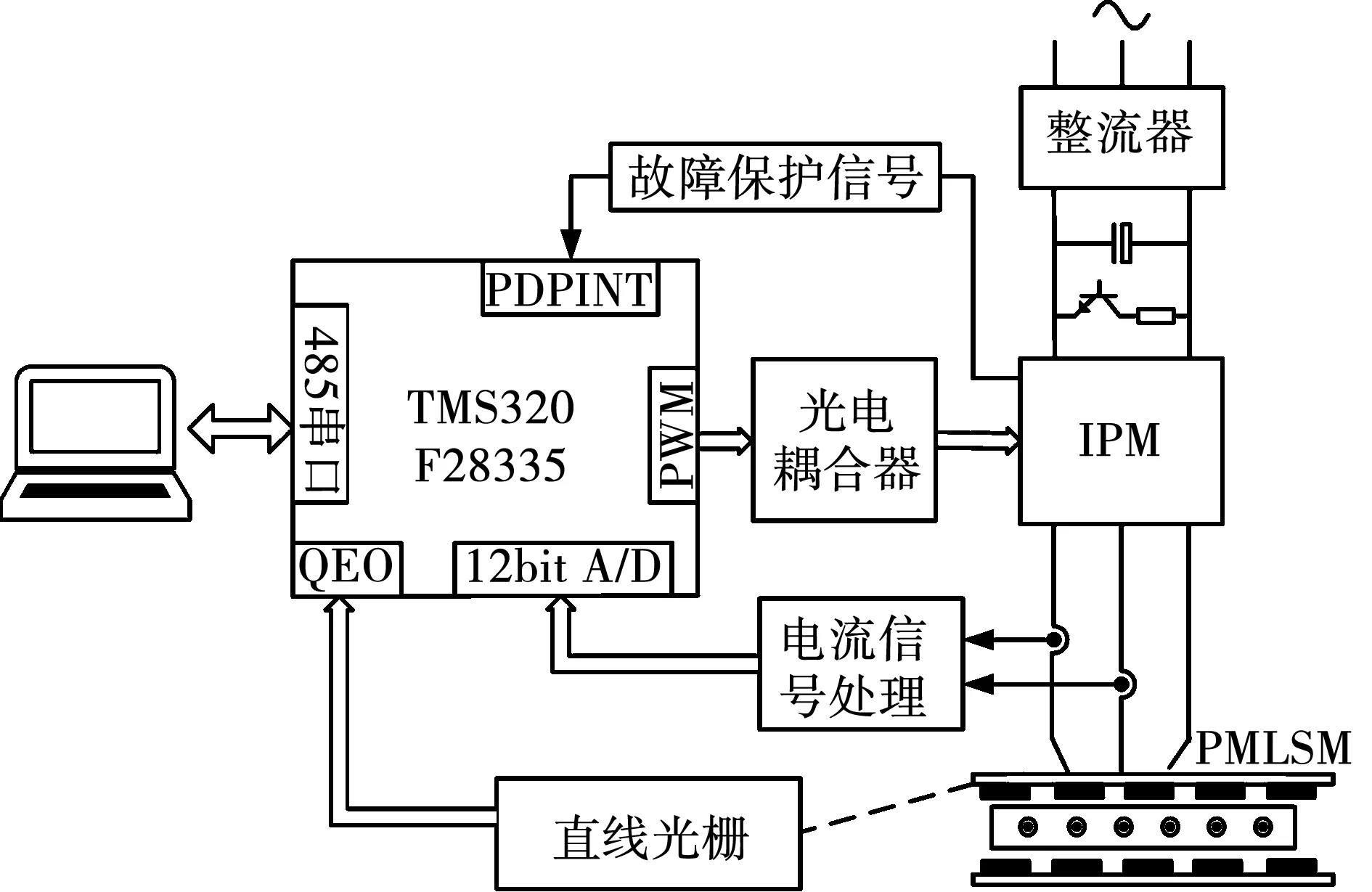
图8 基于DSP的PMLSM控制系统硬件结构图Fig.8 Hardware block diagram of PMLSM control system based on DSP

图9 基于DSP的PMLSM实验系统实物图Fig.9 Photograph of PMLSM experiment systembased on DSP

采用的期望位置输入与仿真实验相同，并在稳态后3.4 s时加入50 N负载阻力。图10(a)和图10(b)分别为S-SMC控制和PDL-ASMC速度响应曲线。对比速度响应曲线，在电机起动时，图10(b)相比于图10(a)能更快的到达稳定运行状态；突加负载扰动时,图10(b)相比于图10(a)也表现出更好的鲁棒性。

图10 系统速度响应曲线(正弦信号)Fig.10 Velocity response curve of system(Sinusoidal signal)

图11(a)和图11(b)分别为S-SMC控制和PDL-ASMC位置跟踪误差曲线。可明显看出，在PMLSM起动时，图11(b)比图11(a)的响应速度更快。图11(a)的位置稳态误差控制在±1.47 μm内，突加负载后，位置误差增加到8.64 μm，稳态恢复时间为0.26 s；图11(b)的位置稳态误差控制在±0.52 μm内，突加负载后，位置误差增加到1.97 μm，稳态恢复时间为 0.13 s，仿真结果与试验结果基本一致。因此可看出，当系统受其自身存在的周期性扰动(主要为端部效应和摩擦力)和突加负载扰动时，基于PDL-ASMC控制的永磁直线伺服系统表现出位置跟踪性能更好、误差收敛速度更快，鲁棒性更强的优点。

图11 系统位置跟踪误差曲线(正弦信号)Fig.11 Position tracking error curve of system(Sinusoidal signal)

当采用图12所示的期望位置输入曲线时，S-SMC控制和PDL-ASMC速度响应曲线如图13(a)和图13(b)所示。图13(b)相比于图13(a)速度响应曲线更平滑，且在速度突变时超调较少。S-SMC控制和PDL-ASMC控制位置跟踪误差曲线分别如图14(a)和图14(b)所示。由图14可以看出，当动子速度突变时，PDL-ASMC策略要比S-SMC策略位置响应速度快。由图14(a)和图14(b)的局部放大图可知PDL-ASMC的位置跟踪误差波动频率和幅值均小于S-SMC的位置跟踪误差，且明显削弱了系统抖振现象。

图12 不规则期望位置输入Fig.12 Irregular expected position input

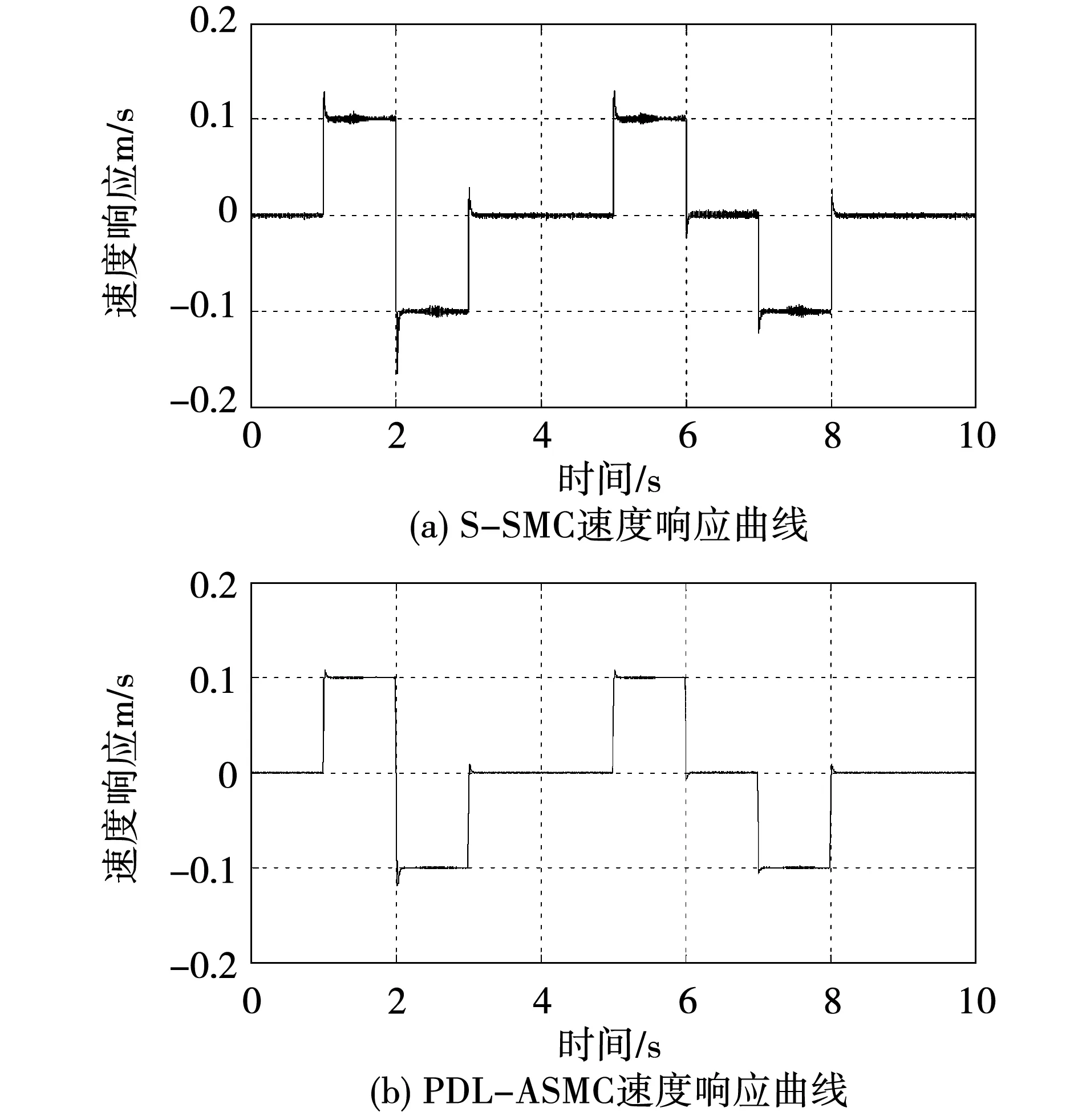
图13 系统速度响应曲线(不规则信号)Fig.13 Velocity response curve of system(irregular signal)

图14 系统位置跟踪误差曲线(不规则信号)Fig.14 Position tracking error curve of system(irregular signal)

由于PDL对端部效应引起的周期性波动有很强的学习能力及滑模控制响应快的特点，使得PDL-ASMC可以更精确地跟踪期望位置输入曲线。

5 结 论

为了提高永磁直线同步电机伺服系统位置跟踪精确度和鲁棒性能，本文提出了一种基于周期性扰动学习的自适应滑模控制器。周期性扰动学习算法能有效处理系统中的周期性扰动。在滑模控制器的设计中综合了周期性扰动学习算法，保证了系统对周期性扰动的抑制。采用自适应算法对系统的非周期性扰动进行估计，减小了最小切换增益，从而削弱了系统抖振。实验与仿真结果表明，在周期性扰动和非周期性扰动状态下，基于PDL-ASMC控制器的永磁直线伺服系统都具有位置跟踪性能好、鲁棒性强和响应速度快的优点。