基于学科核心素养的中职数学公式有效记忆策略研究

张佩丽

摘要：公式是数学学习的基础，但对于中职学生来说，数学学习的困难很大程度上来源于对公式的不理解、记不清。本文旨在通过探究不同数学公式的有效记忆策略，有意识地培养、锻炼、优化学生的记忆品质，激发学生学习数学的兴趣，提升数学核心素养。

关键词：中职数学;公式;记忆策略;核心素养

公式教学是数学教学的一个重要的组成部分，但因其多、繁、复杂而让学生不喜。然而数学公式又十分重要，很多时候它是数学解题的第一步，如果公式不熟记，学生后续解题就会束手无策， 无法深入继续下去。中职数学相对于普高来讲，难度要降低不少， 但仍有很多题目都会考到公式的应用。

一、中职学生数学公式记忆现状

数学公式的记忆是中职学生目前学习中碰到的主要困难，很多学生不愿意记。主要是基于以下原因：一是思想上不够重视，觉得背诵、记忆是文科的专属，数学不需要;二是经常死记硬背，课后又不及时加以巩固，导致很多知识点在应用的时候模糊不清;三是学习兴趣缺失，嫌弃记公式枯燥乏味、细碎麻烦，不愿背诵、记忆， 导致做作业时没有主动思考，也没有认真分析错题，经常犯同样的错。

记忆力是学习的核心，无论要学会什么东西，首先得把它记住—— 只有在大脑里留下了印象的东西，才有可能变成自己的。在数学这门学科中，除了计算能力、空间想象力、逻辑思维能力这三大基本能力之外，数学记忆能力也是一项十分重要的辅助能力，良好的数学记忆能力能帮助学生大幅度提高成绩。因此，本文立足于中职学生特点和思维规律，通过探究不同数学公式的有效记忆方法，有意识地培养、锻炼、优化学生的记忆品质，提高数学公式的记忆效果。

二、中职数学公式记忆策略

在新课标中，数学核心素养被从六个方面进行了解释，这六方面的内容相辅相成，逐渐深入。在学习数学时，想要落实核心素养，就不能从知识的表象出发，而是应该从其内涵着手。运用科学合理的策略记忆数学公式，有助于提升学生数学核心素养， 提高课堂教学质量。

（一）公式推导法

公式推导法重视公式推导、要求学生理解、掌握公式的形成过程的方法，是提升学生逻辑推理素养的有效策略。新课标认为，逻辑推理能够体现出数学的严谨性，是得出数学知识，构建数学体系的重要保障。中职数学，包括数学老师自己，其实并不特别重视公式的推导，很多时候会略过公式的推导，让学生直接记忆公式，应用公式，这就不利于学生理性思维品质和能力的培养。没有理解公式的来龙去脉，只是单纯的死记硬背，短时期内识记少量的公式是没什么问题，但是当整章、整本书学完，公式多时，就会很多公式混在一起，搞不清楚。因此，在教学过程中，应引导学生一起参与公式的推导过程，灵活采用多种教学方式，讲清楚公式原理，这样就算后期忘记公式，学生也能自己推导得出公式以及结论。

又比如，假设等比数列的前n 项和，为q=1 和q ≠ 1，当q=1 时， Sn=na1，q ≠ 1 时，分析等比数列公式的特点，可以得出用错位相减法来求和较为合适。故此，应该先写出 Sn，再两边同乘公比 q， 然后相相关项相减，就可以得到 Sn。在公式教学中，让学生从推理过程着手，让学生熟知公式的全过程，不仅可以让学生真正掌握公式，明白公式的内涵，还能熟练将其运用于解题中。为此， 在教学中，教师就需要从公式的推理着手，如本文所示，在教授数列求和方法时，就可以从倒序相加法和错位相减法着手。

（二）形象记忆法

数学中经常会有较为抽象的知识，这部分知识对于学生的抽象思维以及形象思维都是一种挑战，中职学生在学习时，通常会存在理解不了的现象。此时，将这些抽象的知识，以另外一种较为生动形象的方式诠释出来让学生去理解记忆的方式，则为现象记忆法。这有助于直观想象素养的培育。美国的学者哈拉里是这样强调形象的重要性的，“千言万语不及一张图”。心理学实验发现，此种模式远比让学生直接记忆抽象的公式，要更有利于学生学习知识。故此，在让学生记忆抽象知识时，应该尽量将其以形象的事物来呈现。

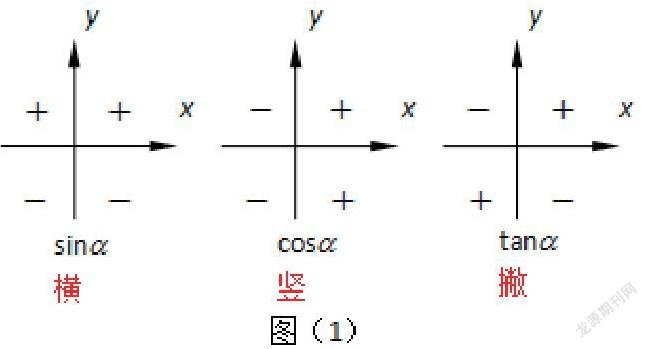
【例2】我们在学习任意角的三角函数定义时，如何记忆正弦、余弦、正切的值在四个象限的符号。任意角的三角函数值的正负号如下图（1）所示 .

“sinα”是第一、二象限为正，三、四象限为负，“cosα” 是第一、四象限为正，二、三象限为负，“tanα”是第一、三象限为正，第二、四象限为负。可先让学生进行观察，能够发现这三个三角函数都是二个象限内为正，二个象限内为负，所以只要记住正的两个，那么剩下的两个象限就是负的，然后引导学生将两个“正”的连起来，发现“正弦”对应汉字笔画中的“横”，“余弦”对应笔画中的“竖”，“正切”对应笔画中的“撇”，对应的汉字就是“才”，（见图 2）这样一个“才”字就可以很形象的将正弦、余弦、正切在四个象限的符号记住。

【例 3】特殊角三角函数的值，在《三角函数》的学习中， 这是基础知识，我们可以用上下楼梯的方法进行记忆。

下图为学生需要掌握的重点知识。由此可找到一些规律，“大于取两边，小于小的，大于大的;小于取中间”来帮助记忆的， 学生先前已经对这个口诀很熟悉了，再次用到这个口诀，可以事半功倍。

巴普洛夫认为，记忆并不是凭空出来的，它需要联想。而这个联想的过程，就是通过知识间的内在联系将新旧知识进行整合，并以全新的方式呈现出来的一个过程。数学公式，有些还是存在着某种的联系的。类比与联想从根本上来说，是一种数学抽象的同样道理，这些特殊角的余弦值，可以看成是下楼梯，如下图4.

（三）“口诀”记忆法

有些比较复杂的公式，难于记住，可对信息进行缩减和编排， 按照韵律提炼成琅琅上口的口诀，在轻松愉悦的氛围中记住公式， 可以大大提高记忆的效果。这种方法其实是在公式数据规律分析的基础上的记忆，口诀记忆的过程一方面是学生知识记忆的过程， 另一方面也是学生对公式进行验证或质疑的过程，有助于提升学生的数据分析素养。

方法。这种由此推彼的记忆方法有利于学生发现数学规律，进而减少记忆负担，提升数学抽象核心素养。利用学生已经学习过的， 容易记忆及印象深刻的数学公式与新学的公式进行对比、联想， 加强学生的记忆效果，能帮助学生更快更好的记住公式。

积公式大家都能記住，在这个基础上乘势引导学生可以把扇形的弧长看成是三角形的底，半径看成是三角形的高，通过类比、联想记忆，这样就可以比较容易记住扇形的面积公式。

【例7】再如数列这一章的学习，在掌握等差数列的性质之后， 可以根据等比数列的定义，去理解记忆等比数列的性质。比如等差数列的性质：若 m+n=p+q 则 am·an=ap·aq，等比数列的性质： 若 m+n=p+q，则 am·an=ap·aq，通常会让学生借助文字记忆，若序号之和相等，则所在项的和相等;而到了等比数列这里，就是序号之和相等，所在项的积相等。通过类比比较，再结合习题的练习，学生就比较容易记住公式。

记住公式的方法有许多，教师在平时要善于总结，教给学生一些巧妙的记忆方法。当然，最好的记忆方法也比不上实践出真知， 记住公式只是数学学习的开始，我们学习数学知识并不是为了记忆公式，而是能够真正用所学公式去解决生活、工作中的一些难题。因此，在解题的过程中，要引导学生进一步熟悉公式以及应用， 以助其更好地理解公式。在理解的基础上，再加上一些行之有效的方法，有利于激发我们中职学生的学习兴趣，进而提升数学成绩。

参考文献：

[1]闫虎 . 提高数学记忆教学效果的策略研究 [J]. 黑龙江：科普童话新课堂，2017（31）.

[2]陈具才 . 讲究记忆方法，优化记忆品质 [J]. 甘肃：中等职业教育，2009（10）.

[3]曹才翰 .《中学数学教学概论》[M]. 北京：北京师范大学出版社，1990.

（绍兴市中等专业学校，浙江 绍兴 312000）