UKF滤波算法在两点边值问题求解中的应用

藏洁，刘升刚

(1.北京空间飞行器总体设计部，北京 100094；2.北京航空航天大学 宇航学院，北京 100191)

0 引言

在最优化问题的间接法求解算法中，根据最优点的必要性条件，原最优化问题转化为一个两点边值问题(two point boundary value problem,TPBVP)，两点边值问题的解就是原问题的最优解[1]。通常两点边值问题所描述的是一个有限维动力系统，在其有限的单维自变量区间的2个端点上存在与系统维数相同个数的若干约束，要求求解满足上述约束的系统状态的时间轨迹。

约束是分别施加于2个端点，故这2个端点的状态都存在一定的自由度。两点边值问题求解的关键就是寻找2个端点状态之间精确的定量关系，或者具有足够精度的近似关系。不过除了十分简单的情况，一般来说从原最优化问题转化得到的两点边值问题所对应的系统都是比较复杂的非线性系统，自变量区间2个端点处的系统状态之间的关系都是具有高敏度、高非线性特性的，且很难得到解析表达式。现在主流的两点边值问题求解算法都是数值求解算法，基本可分为2类:打靶法(shooting method)和转录/配置法(transcription/collocation)[2]。

打靶法的设计变量是考虑始端约束条件下，始端自由状态变量，通过数值方法计算得到终端系统状态变量以及终端状态变量相对始端状态变量的雅可比矩阵，然后根据终端状态约束和雅可比矩阵计算始端状态的修正量，由此迭代重复进行上述计算，直至终端约束满足，得到两点边值问题的精确解[3-5]。打靶法中终端状态和始端状态之间定量关系是对原系统的一阶线性近似，对于高敏度高非线性特性的系统模型，要求打靶迭代的状态初始猜测值具有较高的精度，否则难以收敛到精确解。为了降低系统敏度对打靶法的影响，提高打靶法的鲁棒性，在此基础上发展了多重打靶法[6]，将系统状态轨迹分为若干段，相邻段之间需要满足连续性约束条件[7]，每一段内采用打靶法求解。多重打靶法降低了模型敏度，提高了鲁棒性，但本质上并没有解决打靶法对状态初值敏感的问题，并且引入额外的设计变量和约束。

转录/配置法[8-9]将自变量在取值区间上离散化，以所有离散节点所对应的系统状态变量为设计变量，节点之间的状态变量通过多项式插值得到。在自变量区间上选择配置点，要求在配置点上满足系统的动力学方程，这实际上是有限维的等式约束，由此将动力系统的动力学方程约束转化为代数方程约束，同时考虑原问题的边值约束，将两点边值问题转化为一个非线性规划问题[7,10]。为了保证在配置点上的导数计算精度，一般采取Hermite-Simpson插值方法[11]计算系统状态变量的导数。与打靶法相比，打靶法在求解过程中始终保证满足系统动力学方程，而转录/配置法在求解过程中不能保证满足系统动力学方程，一般不需要进行大计算量的数值积分，但是其设计变量维数大大增加，并且同样存在对状态初值敏感的问题。

针对目前两点边值问题求解算法对初值十分敏感、难以收敛的问题，本文提出基于UKF(unscented Kalman filter)滤波算法的新的两点边值问题求解方法。其基本思路是将原动力系统随机化，假设系统状态变量都满足高斯分布，将原两点边值问题转换为一个最优参数估计问题。采用Unscented变换，可以根据系统始端状态变量的概率分布，得到经过非线性变换后系统终端状态变量概率分布的二阶以上精度近似，由此得到系统始端状态变量和终端状态变量之间二阶以上精度的定量关系。采用UKF滤波算法，可以递推修正系统始端状态，直至滤波收敛，得到原两点边值问题的解。由于此方法对系统的近似描述具有二阶以上精度，直观上可以确定其收敛域要远大于上述仅仅具有一阶精度的传统求解方法，对状态初值敏感的程度大大降低。

1 Kalman滤波和Unscented Kalman滤波算法简介

目前，估计理论主要有三大类方法:最小二乘估计、极大似然估计和贝叶斯估计。从最小二乘法和贝叶斯估计出发，在一定假设条件下，都可以推导出Kalman滤波。从最小二乘法理论理解，Kalman滤波本质上是线性系统的线性最小方差估计；从贝叶斯估计理论理解，Kalman滤波本质上是高斯线性系统的序列Bayes估计[12-13]。通常贝叶斯估计需要相关变量完整的概率分布描述，在高斯分布的假设下，只需要变量的均值、方差和协方差即可。最小二乘估计(最小方差估计)只需要变量的均值、方差和协方差，但精确的最小方差估计求解比较困难，以线性最小方差为目标，可以采用Hilbert空间投影定理直接求解。

考虑在状态空间中描述的一个离散系统，

(1)

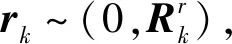
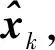
(2)

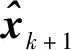
若式(1)是线性系统的情况，上述递推线性最小方差估计的实现(很容易计算随机变量经线性变换后的均值和协方差)就是Kalman filter(KF)。对于式(1)是非线性系统的情况，产生的困难是准确计算随机变量经非线性变换后的均值和协方差。Extended Kalman filter(EKF)是将非线性系统近似为一阶线性系统，但精度较低。Unscented Kalman filter(UKF)由Julier首先提出[14]，是在Kalman filter基础上增加了UT变换(unscented transformation)，专门处理非线性系统的最优估计问题。

UT变换可以得到随机变量经非线性变换后二阶精度以上的均值和协方差，基本思想是近似非线性函数的概率分布比近似非线性函数本身更容易，它采取一定规则的Sigma采样点集合S来表征随机变量的基本统计特征，然后对所有Sigma点进行非线性变换，通过加权计算非线性变换后的随机变量的基本统计特征。这种方法不依赖于非线性函数的具体形式，关键在于采样策略，即Sigma点的个数，分布和相应的权值。

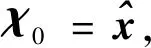
(3)

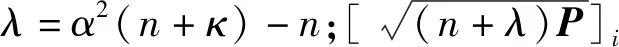
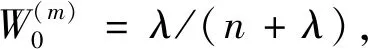
(4)

将所有的Sigma点进行非线性变换G处理，

(5)

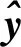
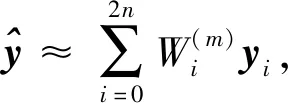
(6)

上面公式中一些常数的含义如下：

(2)常量κ≥0，以保证方差矩阵的半正定性，一般取为0或者3-n。

(3)β是与x的先验分布相关的常量，对于高斯分布，β=2是最优的。对于非高斯分布，这个参数还可以用来控制误差。

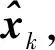
(7)

不考虑系统噪声，经式(1)非线性变换，

(8)

xk经过(1)作用后的均值和方差为

(9)

(10)

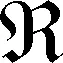
(11)

不考虑观测噪声，经式(1)非线性变换，

(12)

根据UT变换，

(13)

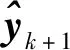
(14)

而xk+1和yk+1的协方差矩阵为

(15)

对于线性最小方差估计，

(16)

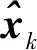
(17)

KF和UKF本质上都是高斯系统的线性最小方差估计(只需要随机变量概率密度分布的一阶矩和二阶矩即可计算最优估计)，而KF是线性系统的精确实现，UKF是非线性系统二阶精度以上的实现。滤波过程的核心是计算相关变量的方差矩阵，只有正确计算方差矩阵才能保证滤波的收敛性和无偏性。系统状态变量的方差分为2部分，之前时刻变量方差的传递和当前系统噪声的影响。之前时刻的状态变量方差体现了对状态变量先验知识的了解，系统的噪声体现了对模型先验知识的了解。在实际应用中，系统模型是不可能完全精确建模，为了弥补模型和真实情况的偏差，必须给定合适的系统噪声，以体现这部分的影响，否则滤波器没有足够的增益对状态变量进行更新修正，导致滤波发散，具体的体现可能就是状态变量的方差很小，但滤波结果远偏离实际值。适当增加系统噪声的方差，可以增加滤波器的稳定性[15]，降低对状态初值的敏感性，但是这会降低模型的预测精度，增加滤波结果的误差。从另一角度来理解此结论，Kalman滤波发散是由于模型的偏差使得只能在短时间内保证预测正确性，而Kalman滤波算法是根据全部的测量预测结果来估计当前的状态。增加系统噪声方差，使得在滤波过程中，更早的观测数据会更快地被舍弃掉，而给最近的观测数据赋予更大的权值，由此可以避免滤波发散。

2 UPE算法简介及其在两点边值问题求解中的应用

UPE，即UKF parameter estimation。假设存在非线性映射，

yk=G(xk,w),k=1,2,…,∞,

(18)

式中：(xk,yk)为已知的映射对序列；w为一组未知的参数，参数估计即根据上述非线性映射和映射对序列，估计未知的参数w。将非线性映射进行如下变换：

(19)

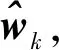
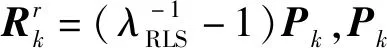
这2种方法思路都是在滤波初段设置较大的系统噪声方差，保证滤波收敛，在滤波后段使得系统噪声方差减小，保证滤波精度。算法流程如下：

(1)初始化

(20)

(2)状态更新

对于k∈{1,2,…,∞}状态更新和Sigma点计算

(21)

Yk|k-1=G(xk,Wk|k-1),

(22)

(3)观测更新

(23)

两点边值问题也可以看作一个参数估计问题。存在如下动力系统，

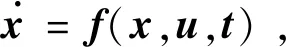
(24)

式中：x为n维状态变量；u为给定驱动，在时间区间t∈[t0,tf]上分析系统响应。时间区间2个端点的状态变量记为x0=x(t0)和xf=x(tf)，当给定x0即可根据式(24)确定xf，xf可记为x0的函数xf=g(x0)。假设对x0存在k个约束，对xf存在n-k个约束，形式为

(25)

上述即为常用的两点边值问题完整描述。由式(25)可以消除x0的k个自由度，假设余下的n-k个自由度记为w，x0可记为w的函数x0=h(x)。式(25)的终端约束可以变换为

0=G(w)=Gf(g(h(w))).

(26)

式(26)可看作一个参数估计问题，和式(18)相比，xk隐含在w中，yk恒等于0，可以采用UPE算法得到两点边值问题的解。

3 算例

考虑高超声速飞行器上升段飞行过程，动力为固体火箭发动机，采用纵向平面内动力学方程，不考虑地球自转和弧度，忽略控制系统延迟，根据瞬时平衡假设，归一化的质心动力学方程为

(27)

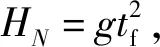
(28)

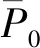
气动力为

(29)

(30)

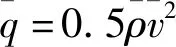
Cx=(a2M2+a1M+a0)+(b2M2+b1M+b0)α2，

(31)

Cy=(c2M2+c1M+c0)+(d2M2+d1M+d0)α,

(32)

式中：M为马赫数；α为攻角；ai，bi，ci，di为常系数。

初始边界为

(33)

终端边界为

(34)

优化指标为

(35)

(36)

协态方程为

(37)

式(37)右端下标代表对应偏导数，具体形式略。最优控制α*使得沿最优轨迹哈密尔顿函数最小，满足必要条件，

(38)

将式(29)～(30)代入式(38)，得

(39)

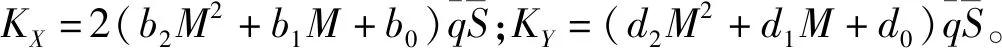
式(39)可能存在多解，需要确定使得式(36)最小的值。将式(39)再次对α求偏导

Hαα=k1sinα+k2cosα+k3=

(40)

式中：k1，k2，k3对应相应的系数。

如果式(40)无解，那么式(39)只有一个解，如果式(40)有解，将其记为

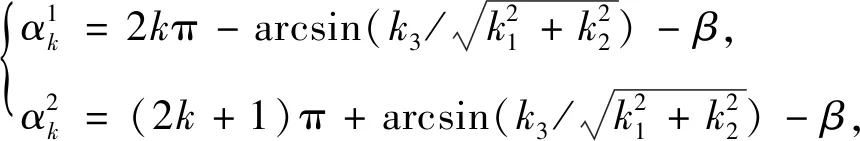
(41)

式中:β定义如下：

(42)

横截条件为

(43)

组成了两点边值问题的描述。算例初末状态见表1。

表1 初末轨道要素和计算参数Table 1 Elementary and final orbital elements and calculation parameters

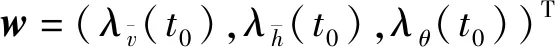
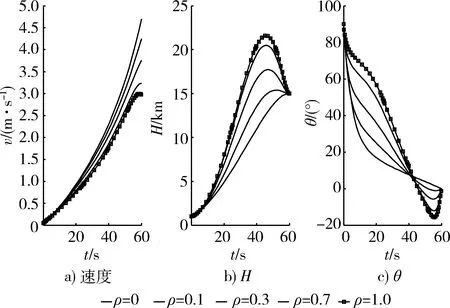
图1 考虑不同大气影响下状态变量时间历程Fig.1 Considering the time history of state variables under different atmospheric influences

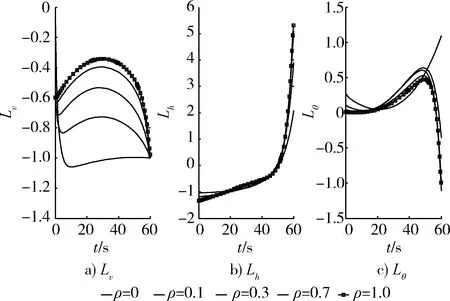
图2 考虑不同大气影响下协态变量时间历程Fig.2 Considering the time history of co-state variables under different atmospheric influences

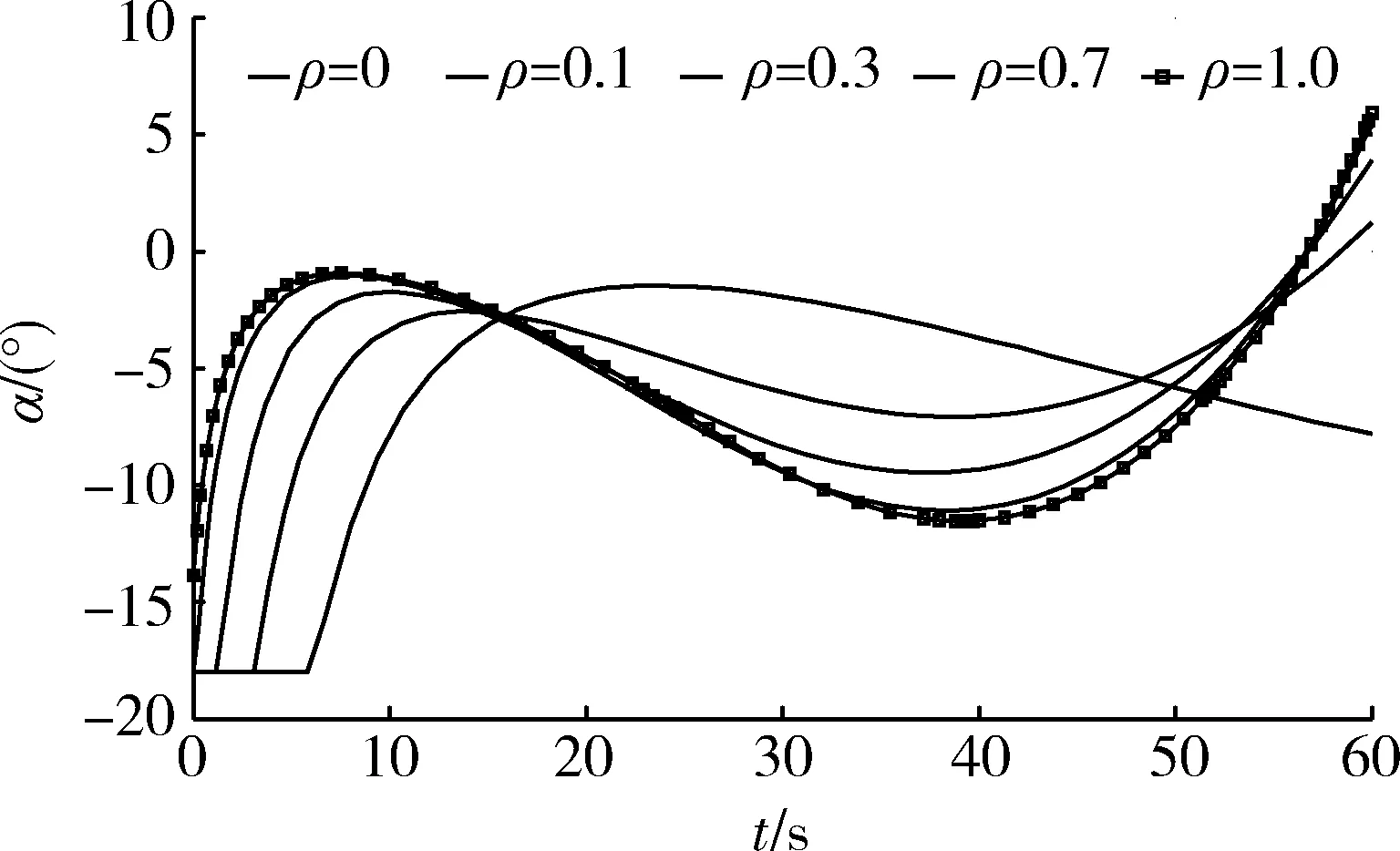
图3 考虑不同大气影响下控制变量时间历程Fig.3 Considering the time history of control variables under different atmospheric influences

根据仿真结果，所有的边界条件和最优必要条件都满足。对于本文给定末端条件的显著特点是，有大气影响时末速最大的弹道并不是直接达到给定的15 km高度，而是尽快达到较高的高度，然后下滑拉平。从物理意义来看，在具有足够的爬高能力时，快速达到较高的高度，可以显著减少气动阻力损失，增大最终末状态的能量。

4 结束语

UPE是基于UKF的参数估计方法，适用于非线性模型的参数估计问题，具有较大的收敛域。两点边值问题可以转化为一个非线性参数估计问题，因此可以采用UPE进行求解。与传统的两点边值问题求解算法相比，其收敛域更大，对初值精度要求不高，因此大大降低了两点边值问题的求解难度。

两点边值问题在诸多科学问题中都有涉及，特别是间接法最优化问题中，最终将最优化问题转化为一个两点边值问题来求解，这在航空航天器轨迹优化与最优制导中应用广泛。本文给出的算例，验证了UPE算法求解两点边值问题应用在轨迹优化中的可行性和优越性，但对于大气层内的轨迹优化问题，仍存在一些不足之处需要改进。

后续研究方向主要分为3个方向：①UKF滤波的方差初值和根据滤波情况自适应调整系统方差的算法；②UPE算法在直接法最优化问题中的应用；③粒子滤波算法在两点边值问题中的应用。