坐标观测值的《误差理论与测量平差基础》教学内容设计

刘志平 李洪娜 汪林根 仇春平

(1. 中国矿业大学 江苏省环境资源信息工程重点实验室, 江苏 徐州 221116; 2. 中国矿业大学 环境与测绘学院, 江苏 徐州 221116)

0 引言

《误差理论与测量平差基础》(简称《经典平差》)是测绘工程专业核心课程之一,在该专业本科教学体系中占有非常重要的地位,也为后续研究生阶段的学习提供先修基础[1-3]。由此,《经典平差》课程教改研究一直受众多同行关注,其中部分研究成果专注于教学模式、方法与形式革新[4-6]。然而,若按一流本科课程(“金课”)建设标准,则亟须关注《经典平差》教学内容本身的创新研究[7]。也正因此,许多学者围绕测量平差中矩阵算子作用[7]、多余观测值剖析[8]、测量平差模型的完善[9-11]、虚拟观测值的理解[12]、多维观测值的平差方法[13-14]等进行了有益的教学内容改革尝试。当前,本专业在不断吸收测绘新理论、新技术以适应新时代发展和专业课程教学学时不断压缩的双重背景下,《经典平差》课程的重视程度在本专业相对下降[7],正成为该课程教学在将来面临的主要挑战,即“存量更新、增量补充”问题。

作者认为导致这种状况的主要原因在于《经典平差》课程教学案例陈旧、类型单一、可迁移性弱,同时在处理与后续专业课程关系时易陷入首鼠两端。例如,水准网、三角网和导线平差(对应高差、角度和边长一维观测值)等至今仍然是主要教学案例,然而大量照搬《大地测量学基础》《摄影测量原理》《GNSS测量原理》《工程测量学》《GIS原理》等核心专业课程中的测量平差问题又会产生重复教学矛盾。鉴于此,本文立足于测绘类专业的高精度、高可靠位置服务这一本质,牢牢抓住“坐标观测值”的测量平差问题作为测绘类核心专业课程的有机联系,试图围绕点、线、面构建二维平面、三维空间中的多种坐标观测值方程,既丰富了《经典平差》教学案例的内容类型、增强了可迁移性,又避免了与后续核心专业课程的重复教学矛盾。与此同时,深入探讨了坐标观测值平差模型属性特点,揭示了现有教材中关于多余观测数计算存在的不足,为《经典平差》教学内容革新提供了新思考。

1 二维平面的坐标观测值方程

1.1 椭圆方程

在高斯平面坐标系中,设椭圆上的坐标观测值为(x,y),椭圆圆心坐标参数为(x0,y0),旋转角参数θ,二维半轴参数为(rx,ry),则可写出坐标观测值表示的二维平面椭圆方程

(1)

进一步,对式(1)进行整理化简可得椭圆的二元二次方程

Ax2+By2+Cxy+Dx+Ey+F=0

(2)

特殊地,当θ=0,rx=ry=r,则式(2)退化为二维平面的圆方程

x2+y2+D′x+E′y+F′=0

(3)

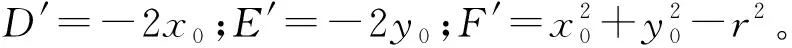
分析式(1)可知,确定平面椭圆位置、大小、形状的必要参数为5个。式(2)中含6个参数,表明参数之间相关且有1个非必要参数。一般可采用A=1,B=1或者A2+B2=1等的限制条件。分析式(3)可知,确定平面圆位置、大小的必要参数个数为3,与式(3)的参数个数相同,表明参数之间不相关。此外,当有N个坐标点,则坐标观测值个数为2N,一般条件方程个数为N。

1.2 共线方程

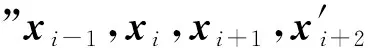
(4)

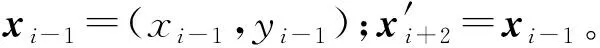
分析式(4)可知,若有N个二维坐标点满足同一共线条件,则坐标观测值个数为2N,一般条件方程个数为N-2。进一步分析可知,式(4)本质上为平面坐标共线的条件平差方法。若利用间接平差方法,平面直线拟合仅需要2个必要参数。

1.3 方位方程

设xi=(xi,yi),xj=(xj,yj)分别为高斯平面坐标系下的两个点坐标,当已知它们与某中心站点x0的已知夹角为αij,则可列立坐标观测值表示的已知夹角方程

(5)

分析可知,当α=0°或α=180°,式(5)实际上表示xj、x0、xi满足三点共线条件;当α=90°,式(5)实际上表示直线(x0,xj)与直线(x0,xi)满足正交条件。此外,当直线(x0,xj)与坐标纵轴平行,则式(5)实际上表示(x0,xi)的坐标方位角。此时,对于已知站点x0与N个坐标点可形成N个已知方位Ai,则坐标观测值表示的已知方位方程

(6)

分析式(6)可知,对于中心站点x0和N个坐标点xi,若已知相应的N个已知方位Ai,不考虑中心站点坐标误差的情况下,则坐标观测值个数为2N,一般条件方程个数为N。

1.4 平行四边形方程

在高斯平面坐标系中,设四边形中按逆时针编号的4个角点坐标分别为x1=(x1,y1),x2=(x2,y2),x3=(x3,y3),x4=(x4,y4),为了将该四边形修正为平行四边形,则需根据平行四边形的任意一个判定条件:(1)对边相等;(2)对角相等;(3)对边平行条件;(4)中心对称图形。建立相应的坐标条件方程

(7)

(8)

(9)

x2+x4=x1+x3

(10)

式(7)～(10)分别为以距离表示的对边相等方程、以角度余弦表示的对角相等方程、以零行列式表示的平行方程和以对角线中心重合表示的中心对称方程。显见,式(10)为线性方程,其余均为非线性方程,表明通过适当的参数选取方式可有效简化方程复杂性或者降低平差模型复杂性。进一步,若需要获得平行四边形的中心坐标参数xc,则可重新列立包括4个角点坐标和1个中心坐标在内的一般条件方程

(11)

分析式(11)可知,对于4个角点的平行四边形修正要求,在选取1个中心坐标作为参数的情况下,则坐标观测值个数为8,一般条件方程个数为4。

1.5 坐标转换

设xI=(xI,yI)T和xII=(xII,yII)T分别为两个不同高斯平面坐标系下的某公共点二维坐标,则它们存在如式(12)的坐标转换关系[14]

(12)

式中,k为尺度参数;θ为旋转角参数;dx,dy表示平移参数。

分析式(12)可知,必要参数个数为4。若有N个公共坐标点,在仅假设源坐标系下坐标没有误差的情况下,则坐标观测值个数为2N,一般条件方程个数为2N。

2 三维空间的坐标观测值方程

2.1 椭球方程

将二维平面拓展到三维空间,可以参考式(2)直接写出三维椭球的三元二次方程

(13)

特殊地,若三维半轴相等时,即rx=ry=rz=r,则三维椭球退化为三维圆球方程

x2+y2+z2+Gx+Hy+Iz+J=0

(14)

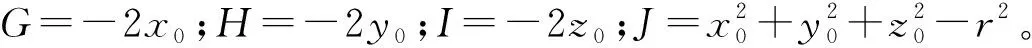
2.2 圆曲线方程

设平面上的某三维坐标记为(x0,y0,z0),该平面法向量记为(a,b,c),则可建立该平面的点法式平面方程。同时,结合三维空间的圆球方程式(14),则可以建立由平面与圆球在三维空间相交而成的三维圆曲线方程

(15)

式中,d=-ax0-by0-cz0。

分析式(15)可知,三维空间的平面式含有4个参数,圆球式含有4个参数。其中,法向量为非零向量,能够通过某种标准化施加1个限制条件,例如a=1,b=1,c=1或者a2+b2+c2=1等。由此表明,平面式仅含3个必要参数,三维圆曲线包括7个必要参数。此外,当有N个坐标点,则坐标观测值个数为3N,一般条件方程个数为2N。

进一步地,若式(15)中的平面穿过圆球的圆心,则需要再增加1个限制条件

a·G+b·H+c·I=2d

(16)

2.3 共面方程

[(xi+1-xi)×(xi+2-xi)](xi+3-xi)T=0

(17)

分析式(17)可知,若有N个坐标点满足同一共面条件,则坐标观测值个数为3N,一般条件方程个数为N-3。进一步分析可知,式(17)本质上为三维坐标共面的条件平差方法。若利用间接平差方法,三维平面拟合仅需要3个必要参数。

2.4 直线方程

根据三维空间的平面方程式原理,当两个不同的平面在三维空间相交的交线则可以形成直线,则由坐标观测值表示的三维直线方程如下[15]

(18)

分析式(18)可知,根据平面法向量不为零向量,则需对两个平面施加2个限制条件,具体限制条件可以参考2.2节。具体地,式(18)中8个参数,包括6个必要参数、2个非必要参数。此外,当有N个坐标点,则坐标观测值个数为3N,一般条件方程个数为2N。

2.5 坐标转换

设XI=(xyz)T和XII=(XYZ)T分别为两个不同空间直角坐标系下的某公共点三维坐标,则它们存在如式(19)的坐标转换关系[16]:

XI=k·R·XII+T

(19)

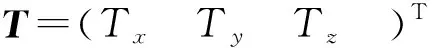
分析式(19)可知,必要参数个数为7。若有N个公共坐标点,在不考虑源坐标系下坐标误差的情况下,则坐标观测值个数为3N,一般条件方程个数为3N。

3 坐标观测值平差模型属性分析

基于第1和第2节的分析,若有N个坐标点,分别按二维椭圆方程式(2)、二维圆方程式(3)、二维共线方程式(4)、二维方位方程式(6)、平行四边形方程式(11)、二维坐标转换方程式(12)和三维椭球方程式(13)、三维圆球方程式(14)、三维圆曲线方程式(15)、三维共面方程式(17)、三维直线方程式(18)、三维坐标转换方程式(19)。若将坐标观测值个数记为n、确定模型的必要参数个数记为t、选取参数个数记为u、一般条件方程个数记为c、限制条件方程个数记为s、模型自由度记为f、多余观测数记为r,并建立相应平差函数模型,则各平差模型的属性数据如表1所示。

表1的建模方式表示利用坐标数据建模的方式。从表1可看出,本文讨论的二维平面、三维空间的坐标观测值平差模型较好地覆盖了《误差理论与测量平差基础》的四种经典平差方法。其中,(1)二维共线、二维方位和三维共面均属于条件平差模型,所选参数个数u=0;(2)平行四边形属于具有参数的条件平差,所选参数独立且个数ut,形成s=u-t个限制条件方程。需指出的是,限制条件个数公式s=max(u-t,0)更具有普适性。此外,通过表1加强认识模型属性数据的规律:即一般条件个数c与限制条件个数s之和等于参数个数u与多余观测数r之和,即c+s=r+u。其中,多余观测数r等价于平差模型自由度f,即r=f=c+s-u。同时,根据限制条件数s=max(u-t,0),可得更具普适性的多余观测数公式r=c-min(u,t)。

表1 N个坐标点的平差模型属性数据

进一步分析表1中二维坐标观测值的平差情形可得:(1)对于二维共线的条件平差模型,多余观测数r=c-min(u,t)=N-2,然而按照现有教材的多余观测计算式,多余观测数r=n-t=2N-2,显然不正确;(2)对于平行四边形的具有参数条件平差模型,多余观测数r=c-min(u,t)=2,与现有教材r=n-t=2结果一致;(3)对于二维坐标转换的间接平差模型,多余观测数r=c-min(u,t)=2N-4,即N>2,与现有教材r=n-t=2N-4结果一致;(4)对于二维椭圆的概括平差模型,多余观测数r=c-min(u,t)=N-5,即N>5,然而按照现有教材的多余观测计算式,则多余观测数r=n-t=2N-5显然不正确。由此显见,当且仅当采用坐标分量建模方式,由于一般条件方程个数与坐标维数成正比,现有教材的多余观测数计算式正确;而当利用非坐标分量建模方式,由于一般条件方程个数与坐标维数没有确定性关系,导致现有教材的多余观测计算式错误。因此,本文多余观测值计算式,同时适用于坐标分量和非坐标分量建模方式。同理,该结论也适用于三维观测值的平差模型,限于篇幅要求不再赘述。综上,本文通过探讨进一步明确了坐标观测值平差模型中多余观测值的内涵,建议将多余观测值计算式改为r=c-min(u,t),其中c表示一般条件方程个数,t表示必要参数个数,u表示所选参数个数。

4 结束语

作者通过《经典平差》多年教学经验发现,随着专业课程专业学时减少和测绘新技术快速发展,该课程近年来面临比较严峻的课程体系“存量更新、增量补充”问题。鉴于此,本文紧紧抓住测绘类专业的位置服务本质,通过构建以二维、三维坐标观测值为研究对象的“点线面”测量平差问题,既拓广了高差、边长和角度一维观测值的传统课程案例边界,又加强了与《大地测量学基础》《摄影测量原理》《GNSS测量原理》《GIS原理》等后续核心专业课程的通用性联系。与此同时,通过5类二维和5类三维坐标观测值平差模型的属性数据分析,指出了现有教材多余观测数计算式存在的不足，并给出了坐标分量和非坐标分量建模方式的多余观测数通用计算式。总之,本文依据“内容为王、通用呈现”的坐标观测值测量平差教学内容设计思路,为持续增强学生在误差理论方面的迁移学习能力提供借鉴。