材料力学、结构力学与弹性力学的位移计算对比
魏鹏云,张 琴
(塔里木大学水利与建筑工程学院水利系,新疆 阿拉尔 843300)
1 引 言
对于土木及水利工程类的本科生来说,基础力学的学习有不小的难度。一般高校的力学课程安排依次是理论力学、材料力学、结构力学及弹性力学,其中,理论力学的研究对象主要是刚体,而材料力学、结构力学及弹性力学针对的则是变形体。材料力学主要讲授的是杆、轴的拉、压、弯、剪、扭问题,结构力学主要针对的是平面杆件结构的内力及变形计算,弹性力学的研究对象更加广泛,获得的力学响应量的结果更加精确。
结构和构件的位移计算是力学类课程的重点教学内容,此部分内容对学生的数学及力学功底有一定的要求,因而会导致很多同学对位移计算望而生畏。比较教学法可以提高教学效果和质量,同一力学课程的比较[1]及力学类课程之间的比较是很有必要的[2]。本文以矩形等截面简支梁受均布荷载作用时材料力学、结构力学及弹性力学各自能够获得的位移解答为例,通过对比分析来探讨这三门力学在位移计算上的区别与联系,从而提升学生的学习热情,加深学生对于这三门力学课程的理解。
2 材料力学关于简支梁受均布荷载时的位移解答
在材料力学中,计算梁的竖向位移(挠度)可采用挠曲线近似微分方程[3]。如图1所示,跨度为l的简支梁受均布荷载q作用,此时的简支梁用其轴线表示。简支梁的抗弯刚度为EI,截面为矩形。
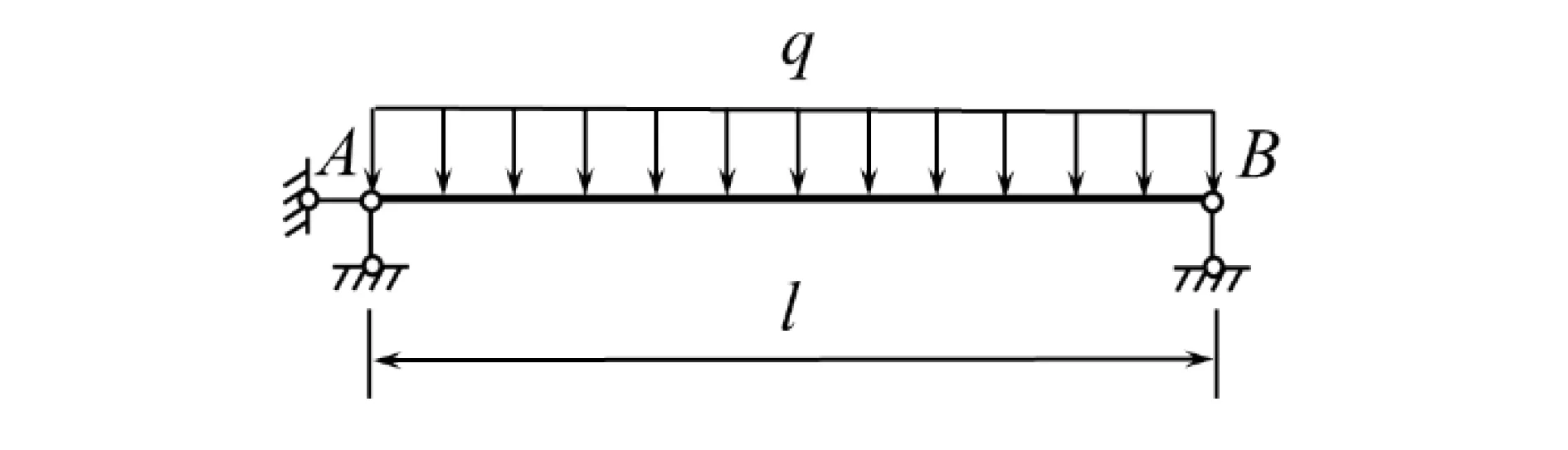
图1 材料力学简支梁计算简图
(1)建立坐标系。以A点为坐标原点,水平向右为x轴正向。
(2)支座反力的求解。由对称性可知:
(1)
(3)任意截面的弯矩方程的求解。从任意位置x处截断,取左侧为隔离体可得:

(2)
(4)梁的挠曲线方程的求解。已知材料力学中等截面直梁的挠曲线方程为:
EIw″=-M(x)
(3)
将式(2)代入式(3)得:
(4)
对式(4)积分一次得:
(5)
对式(5)再积分一次得:
(6)
由简支梁的边界条件可求得积分常数c1和c2:
当x=0时,w=0,将其代入式(6),得c2=0;

将c1和c2代入式(6),可得简支梁受均布荷载作用时的近似挠曲线方程(竖向位移计算公式)为:
(7)
3 结构力学关于简支梁受均布荷载时的位移解答
结构力学计算静定结构位移的一般方法是积分法。此外,对以弯曲变形为主的结构还可以将考虑弯曲变形的积分公式等效为图乘法[4]。因为简支梁是以弯曲变形为主的结构,所以用积分法和图乘法都可以进行计算。为了与材料力学及弹性力学对比,计算位移时要考虑剪切变形的影响,故本文利用积分法来进行推导。一般结构力学教材中计算的结构位移主要是某点的线位移和某截面的角位移以及相对线位移和角位移。要想获得如同材料力学一样的轴线处任意一点的位移计算的解析式,只需要让某点C的位置是任意的即可。
如图2所示,跨度为l的简支梁受均布荷载q作用,为了获得简支梁任意截面的线位移和角位移,可令任意截面C离A支座的距离为a,离B支座的距离为b,则求解出的C截面的线位移ΔC即是简支梁任意截面的线位移。简支梁的抗弯刚度和抗剪刚度分别为EI和GA,截面为矩形。

图2 结构力学简支梁计算简图
(1)建立坐标系。以A点为坐标原点,水平向右为x轴正向。
(2)写出实际荷载作用下任意截面x处的弯矩、剪力方程,做出实际荷载作用下简支梁任意位置x的示意图,如图3所示。

图3 实际荷载作用下任意位置x示意图
利用截面法从x截面截断,取左部分为隔离体,可得弯矩方程和剪力方程。
弯矩方程:
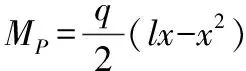
(8)
剪力方程:
(9)
(3)写出虚设单位荷载作用下任意截面x处的弯矩、剪力方程,做出虚设单位荷载作用下简支梁任意位置x的示意图,如图4所示。

图4 虚设单位荷载作用下任意位置x示意图
当0≤x 弯矩方程: (10) 剪力方程: (11) 当a≤x≤l时,利用截面法从x截面截断,取右部分为隔离体,可得弯矩方程和剪力方程。 弯矩方程: (12) 剪力方程: (13) (4)利用积分公式计算ΔC。荷载引起的静定结构位移计算一般公式为: (14) 将式(8)-式(13)代入式(14)得: (15) 为了与材料力学的解保持一致,可用x替换a,则有: (16) 如图5所示,简支梁的截面为矩形,高为h,跨度为l,不计体力。为计算方便,取梁的宽度为单位宽度,受均布荷载q作用,支承处的反力ql/2来维持平衡。 图5 弹性力学简支梁计算简图 (1)构造应力函数并求应力分量。梁的上边界和下边界为大边界,必须严格满足边界条件: (17) 梁的左边界和右边界为小边界,可利用圣维南原理列边界条件: (18) 满足式(17)和式(18)的边界条件的应力函数是具有5次方多项式的函数[5],即为: (19) 根据应力与应力函数的关系可求得应力分量为: (20) (21) (22) (2)确定应力分量中的各系数,获得应力解析式。考虑到σx关于y轴对称,则有式(20)中x的奇次方项的各系数为0,即: c3=d4=c5=e5=0 (23) 由于σy是挤压应力,其与x无关,则有式(21)中含x项的各系数为0,即: a3=a4=b4=b5=a5=0 (24) 由于剪应力(τxy)y=±h/2=0,由式(22)可知: b2=c4=0 (25) 结合式(19)及式(23)-式(25),可得应力函数的形式为: Φ=a2x2+c2y2+b3x2y+d3y3+e4y4+d5x2y3+f5y5 (26) 应力函数应满足双调和方程,则有: ▽4Φ=0+2×12d5y+24e4+120f5y=0 (27) 由式(27)可知: (28) 由式(17)的第三式可知: c2=0 (29) 由式(17)的第一、二式可知: (30) 将式(30)的两式相加,可得: (31) 将式(31)代入式(17)的第一式可得: (32) 由式(17)的第三式和式(18)的第四式可得: (33) 将式(33)的第一式代入式(32)可得: (34) 将式(33)的第一式代入式(28)的第二式可得: (35) 剩余的边界条件校核后自动满足。将已求得的各系数代入式(20)-式(22),可得应力分量σx、σy、τxy的解析式为: (36) (37) (38) (39) (40) (41) (3)求位移分量的解析式。将式(39)-式(41)代入由应力表示应变的物理方程后再代入几何方程可得: (42) (43) 同理可得: (44) (45) 将式(43)积分后得: (46) 将式(44)积分后得: +10y4-3h2y2)+f2(x) (47) (48) 要想由式(48)求得f1(y)和f2(x)的具体形式,需要将式(48)作分离变量处理: (49) (50) 对式(49)和式(50)积分后得: f1(y)=k1y+C1 (51) f2(x)=5x4-7.5l2x2-12h2x2-7.5μh2x2+k2x+C2 (52) 由式(48)-式(50)可知: k1+k2=0 (53) 积分常数k1、k2、C1、C2可由边界条件确定。 当x=0,y=0时,由对称性可知u=0,则由式(46)和式(51)可求得: C1=0 (54) k1=0 (55) 再结合式(53)可知: k2=0 (56) 当x=l/2,y=0时,v=0,则由式(47)和式(52)可得: (57) 至此,积分常数k1、k2、C1、C2均已求得,将其代入式(46)及式(47),可获得位移的解析解如下: (58) (59) 式(59)为弹性力学获得的简支梁受均布荷载时的竖向位移的解析式。为了便于与材料力学及结构力学的解答对比,需要求解轴线处任意点竖向位移的解析式。轴线处的y=0,只需令式(59)中的y为0即可,则有: (60) 式(60)即为弹性力学获得的简支梁受均布荷载时轴线处的竖向位移解析式,也就是轴线处的挠度方程。 式(7)为材料力学获得的简支梁受均布荷载时的竖向位移解析式,要想获得转角位移的解析式,只需要竖向位移对x进行微分,则有: (61) 式(16)为结构力学获得的简支梁受均布荷载时任意位置C的竖向位移解析式,要想获得任意截面C的转角位移解析式,只需要任意位置C的竖向位移对x进行微分,则有: (62) 式(58)及式(59)为弹性力学获得的简支梁受均布荷载时任意点的水平与竖向位移的解析式。因为材料力学和结构力学获得的转角位移是轴线处的,为了便于对比,故只求解轴线处任意点的转角位移的解析式,则有: (63) 通过计算简支梁左右端及跨中位置的转角及竖向位移解答来对比说明材料力学、结构力学及弹性力学在位移计算时的区别与联系。表1为转角位移的解答,表2为竖向位移的解答。注意:材料力学和结构力学的左端x=0,而弹性力学的左端x=-l/2;材料力学和结构力学的跨中x=l/2,而弹性力学的跨中x=0;材料力学和结构力学的右端x=l,而弹性力学的右端x=l/2。 表1 三种力学关于简支梁受均布荷载时轴线处转角位移计算对比 续表1 表2 三种力学关于简支梁受均布荷载时轴线处竖向位移计算对比 由表1可以看出,由于对称性,无论是哪门力学,在简支梁左右端点处的转角位移大小相等、方向相反,跨中转角位移为0。由表2可以看出,由于对称性,无论是哪门力学,简支梁在左右端点处的竖向位移为0,跨中位置竖向位移最大。三种力学获得的转角位移和竖向位移解答各不一样,其中,材料力学获得的位移最简单,且材料力学的位移解答是结构力学和弹性力学位移解答中的一部分。 出现这些区别和联系是因为:材料力学利用挠曲线近似微分方程推导时没有考虑剪切变形的影响,所以其获得的解答是最简单的近似解;结构力学虽然考虑了剪切变形的影响,但是利用积分法考虑剪切变形的影响时仍然采用了一些近似处理(如利用平均切应变来代替考虑剪切变形对位移的影响,并且在计算平均切应变时引入改正系数来考虑切应力在截面上的不均匀分布),因而其得到的也是近似解,但是相较于材料力学,其精确度更高一些;弹性力学是严格地考虑了静力学、几何学及物理学三方面条件,并且建立严格的边界条件进行求解,因而其获得的解答是精确解[6]。 本文以矩形等截面简支梁为研究对象,对比分析了材料力学、结构力学及弹性力学获得的简支梁轴线处的竖向位移及转角位移解答。其中,结构力学中利用单位荷载法推导了简支梁任意位置处的竖向位移及转角位移解答,并通过计算简支梁左端点、右端点及跨中位置的竖向位移和转角位移,说明了材料力学、结构力学获得近似解及弹性力学获得精确解的原因。通过本文的推导计算分析,可以帮助学生更好、更深入地了解这三门力学的区别与联系。


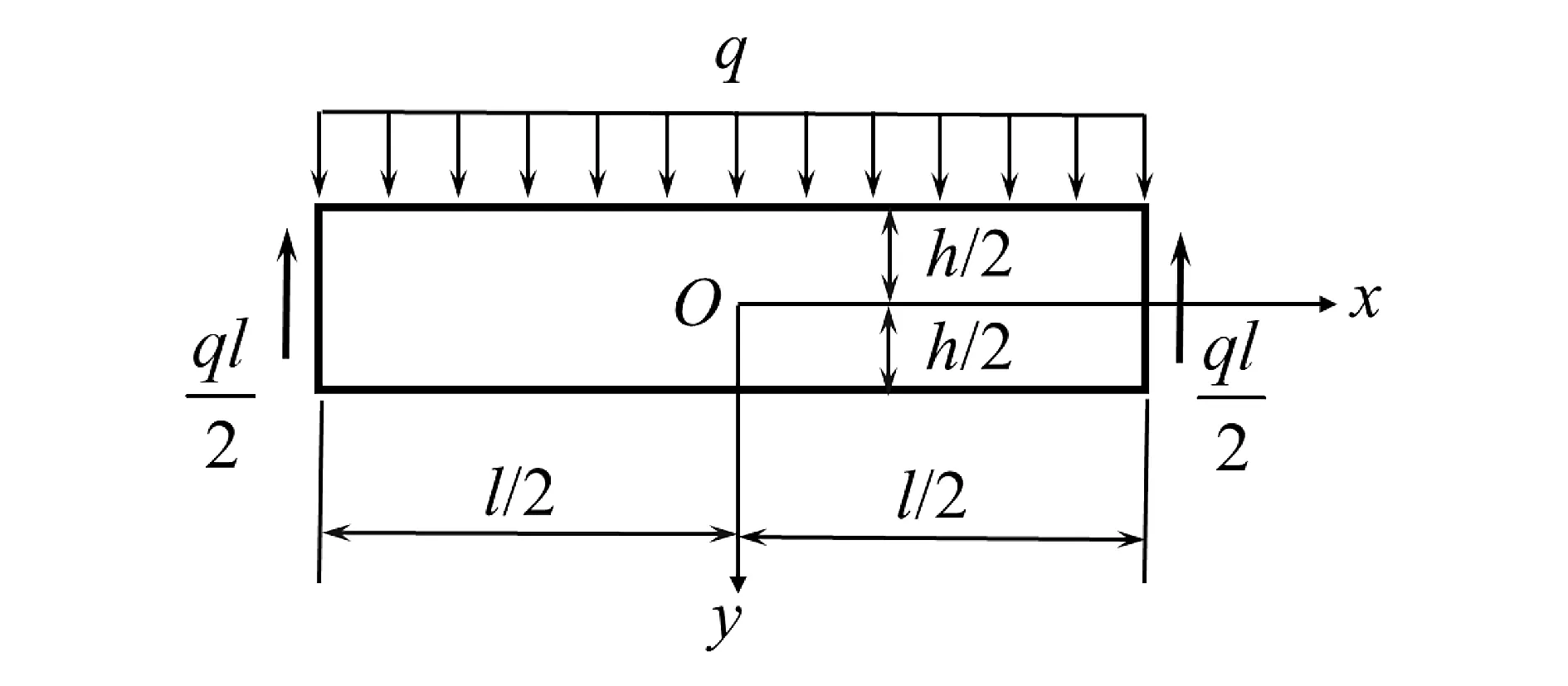
4 弹性力学关于简支梁受均布荷载时的位移解答








5 三种力学关于简支梁受均布荷载时的转角位移解答
6 三种力学关于简支梁受均布荷载时轴线处竖向位移及转角位移解答的对比分析



7 结 语

