剪切效应对工字形梁弯曲挠度影响的分析

王骞弘，吴 晓

(1.湖南城市学院，湖南 益阳 413000；2.湖南文理学院，湖南 常德 415000)

1 引 言

工字形梁在土木工程、铁路交通运输工程等实际工程中有广泛的应用，材料力学教材中给出了工字形梁弯曲正应力、弯曲切应力的计算公式。文献[1]对工字形截面梁弯曲切应力分布进行了讨论，文献[2]对工字形薄壁梁翼缘弯曲切应力进行了分析。文献[3]基于不同梁模型的弯曲变形分析与实验教学探讨，讨论了剪切效应对矩形截面悬臂梁弯曲挠度的影响。文献[4]用材料力学方法研究了不同模量梁的弯曲变形，分析了剪切效应对矩形截面不同模量梁弯曲挠度的影响。文献[5]、文献[6]研究了工字形连续多跨梁结构模型在力学实验教学中的应用，文献[7]讨论了工字形梁的设计。以上文献都没有讨论剪切效应对工字形梁弯曲挠度的影响，所以，研究剪切效应对工字形梁弯曲挠度的影响是有实际意义的。

2 弯曲微分方程

为了不失一般性，以图1所示工字形截面梁为例，研究工字形梁的弯曲问题。

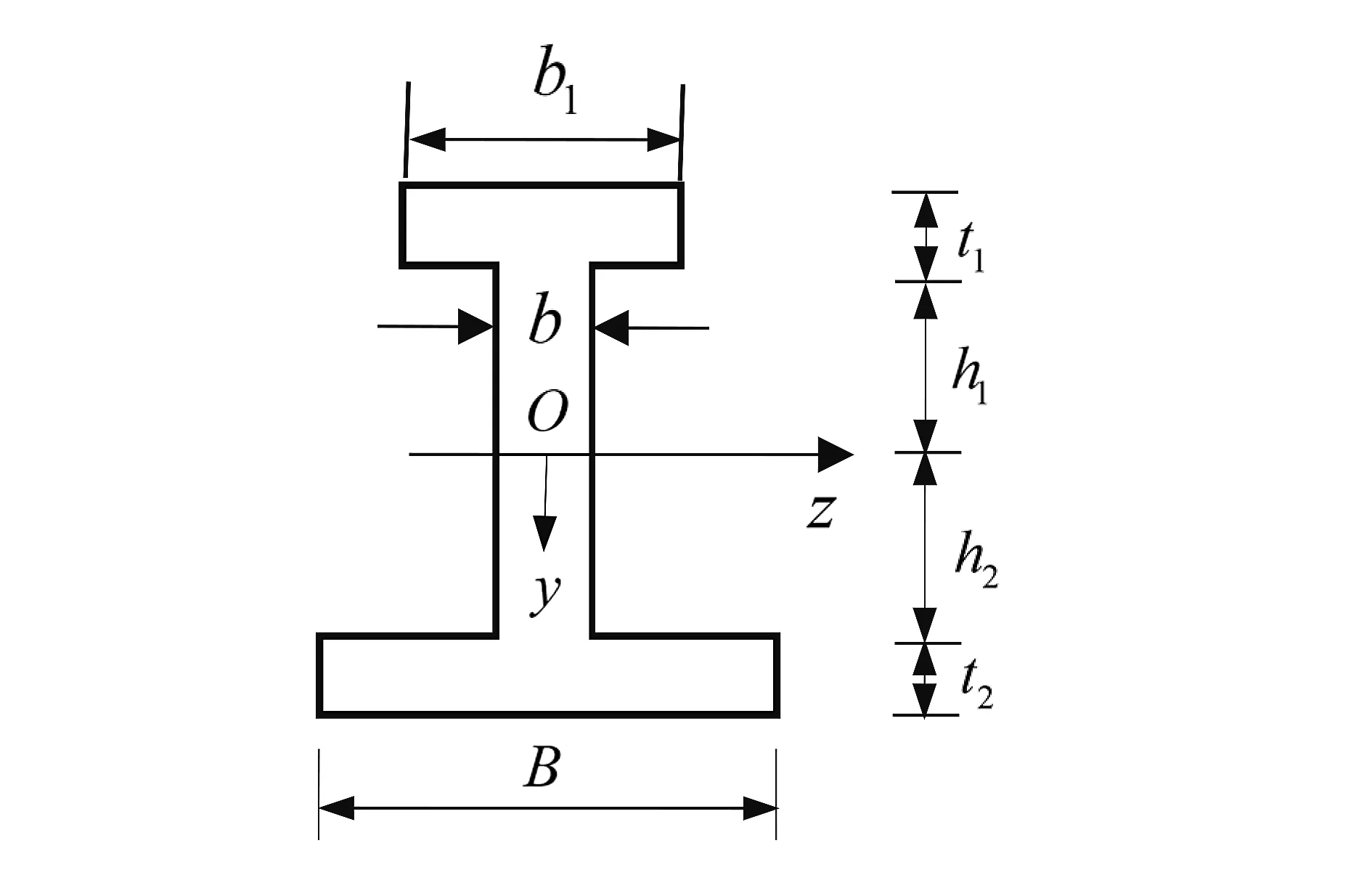
图1 工字形梁截面

由材料力学可知，弯曲正应力为：

(1)

外载荷作用下工字形梁截面轴向静力方程为：

(2)

把式(1)代入式(2)中可得：

(3)

由弹性力学可知，工字形梁截面剪应变与轴向位移、弯曲挠度的关系为：

(4)

式中，γi为剪应变，ui为轴向位移，w为弯曲挠度，τi为剪应力，G为剪切弹性模量。i=1代表上翼缘，i=2代表中性轴以上部分腹板，i=3代表中性轴以下部分腹板，i=4代表下翼缘。

由材料力学可知，工字形腹板承担梁截面剪力的95%～97%，所以材料力学一般假设工字形梁上、下翼缘剪应力为0。因此，本文也认为工字形梁上、下翼缘的剪应力为0，即：

τ1=0，τ4=0

(5)

以图2所示的工字形梁微段为例来推导中性轴以上部分腹板的剪应力τ2。

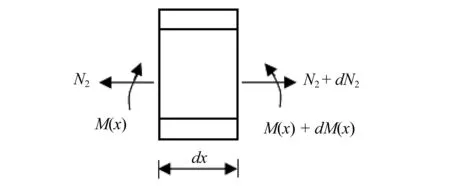
图2 工字形梁微段

中性轴以上部分腹板轴向力为：

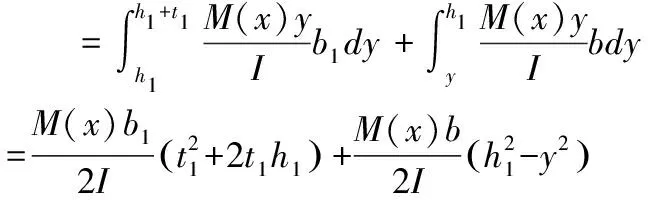
(6)

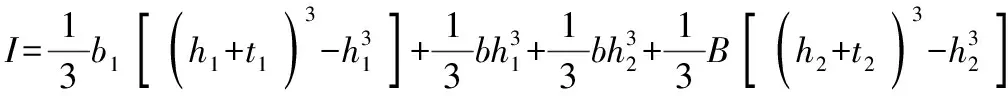
由于静力方程为：

N2+τ2bdx=N2+dN2

(7)

(8)

同理可得中性轴以下部分腹板的剪应力为：

(9)

把式(5)、式(8)、式(9)分别代入式(4)，可得工字形梁轴向位移表达式为：

(10a)

(10b)

(10c)

(10d)

工字形梁轴向位移在中性轴处、腹板与翼缘的连续条件为：

y=0，u2=u3=0；y=-h1，u1=u2；y=h2，u3=u4

(11)

利用式(10)、式(11)可得：

(12a)

(12b)

(12c)

(12d)

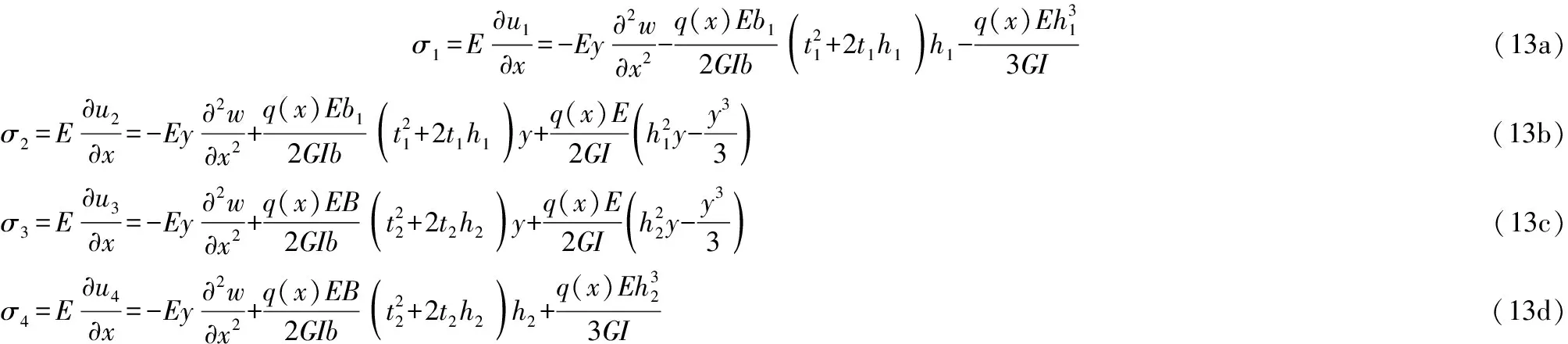
工字形梁截面弯矩平衡方程为：

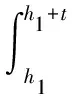
(14)

把式(13)代入式(14)中可得：

(15)

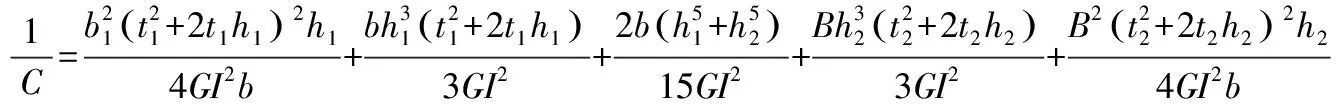
式(15)即为考虑剪切效应时工字形梁的弯曲微分方程。

令t1=0、t2=0时，式(15)积分后得到的矩形截面梁挠度表达式与文献[4]的式(29)是一致的，而文献[4]的式(29)已被验证其计算精度很高且与弹性理论计算结果非常吻合。

3 算例分析

本文通过两个算例来讨论剪切效应对工字形梁弯曲挠度的影响。

算例1。参阅文献[5，6]可知工字形轨道计算参数为：a=0.185m，d=0.295m，b1=2.94mm，t1=2.46mm，b=0.76mm，B=25.76mm，t2=0.88mm，h=28.66mm，E=70GPa，G=26.32GPa，l=0.48m，P=26.15N。

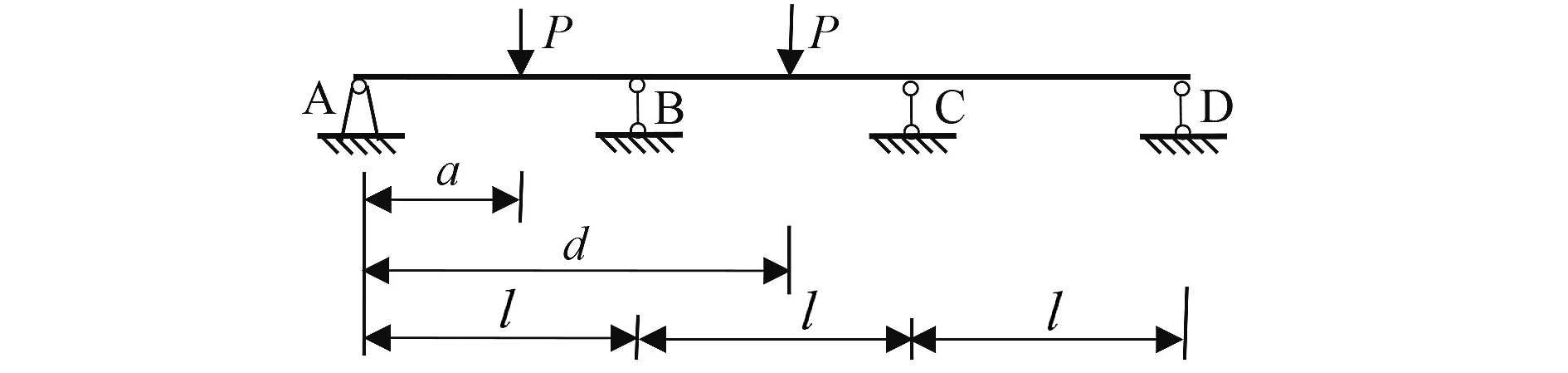
图3 多跨工字形梁

图3所示的工字形连续梁的静力方程为：

RA+RB+RC+RD=2P

(16a)

RBl+2RCl+3RDl=Pa+Pd

(16b)

利用奇异函数可把图3所示梁上载荷集度表示为：

q(x)=RA〈x〉-1+RB〈x-l〉-1+RC〈x-2l〉-1-P〈x-a〉-1-P〈x-d〉-1

(17)

利用奇异函数积分规则可得：

Q(x)=RA〈x〉0+RB〈x-l〉0+RC〈x-2l〉0-P〈x-a〉0-P〈x-d〉0

(18a)

M(x)=RA〈x〉1+RB〈x-l〉1+RC〈x-2l〉1-P〈x-a〉1-P〈x-d〉1

(18b)

把式(17)、式(18)代入式(15)中积分可得挠曲线方程为：

(19)

图3所示梁的边界条件为：

x=0，w(0)=0；x=l，w(l)=0；

x=2l，w(2l)=0；x=3l，w(3l)=0

(20)

利用式(16)、式(19)、式(20)可求得：

RA=0.8102P，RB=1.4284P，RC=-0.2872P，

RD=0.0487P

(21)

把有关参数代入式(19)中可得考虑剪切效应影响时的挠度为：

w(a)=5.8597P×10-6m

(22)

而忽略剪切效应影响时的挠度为：

w′(a)=5.6168P×10-6m

(23)

算例2。由文献[7]可知，图4所示工字形梁的计算参数为：t1=t2=16mm，B=b1=400mm，b=8mm，h=1000mm，E=210GPa，G=80.769GPa，l=8m，P=320kN，q=80kN/m。

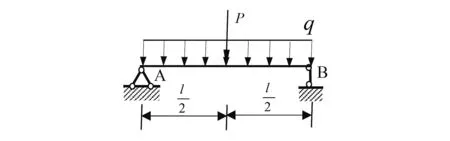
图4 工字形梁

利用式(15)可求得考虑剪切效应影响时梁中点的挠度为：

(24)

而忽略剪切效应影响时梁中点的挠度为：

(25)

材料力学一般认为，梁的跨高比超过5的细长梁挠度计算可以忽略剪切效应的影响；跨高比小于5时，挠度计算才考虑剪切效应的影响。

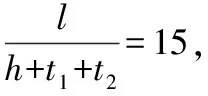
由以上两个工字形梁的计算分析可知，即使在工字形梁是细长梁时，其弯曲挠度的计算有时也不能忽略剪切效应的影响。

由式(13)、式(15)可知，梁在外载荷作用下，分布载荷对梁的应力、挠度都有影响，而集中载荷仅对梁挠度有影响，对梁应力没有影响。

由算例1可知，采用奇异函数计算连续多跨梁的弯曲变形，计算过程清晰简便。

4 结 论

由以上分析可得以下结论：

(1)即使在工字形梁是细长梁时，其弯曲挠度的计算有时也不能忽略剪切效应的影响。

(2)梁在外载荷作用下，分布载荷对梁的应力、挠度都有影响，而集中载荷仅对梁挠度有影响，对梁应力没有影响。

(3)采用奇异函数计算连续多跨梁的弯曲变形，计算过程清晰简便。