探究弦球链系统的拓扑不变量

林织星，王志元，杨天骅

(北京大学 物理学院，北京 100871)

自1980年代起，一系列特殊的材料——拓扑绝缘体得到了持久而广泛的关注，这些材料的边缘态是“拓扑保护”的，其性质取决于体能带本身的拓扑非平庸性，因而受杂质的影响较小，同时其输运系数也可以通过拓扑不变量的计算来定量地衡量[1].

一维弦球链体系作为一个简单、直观、典型的用于模拟晶体中电子系统的力学声子系统，其能谱和本征态已经得到了较为深入而全面的研究[2].而在弦球链的一系列本征态中，边缘态(带隙态)的性质较为特殊，边缘态的存在具有一定的鲁棒性，不受体系参数变化的影响，其局域位置会随着体系参量发生改变，且呈现出一定的规律.近年来，一些利用拓扑绝缘体的能带拓扑理论来研究力学声子体系的边缘态和拓扑性质的工作，印证了能带拓扑理论同样适用于声子体系[3].弦球链体系边缘态与拓扑绝缘体边缘态在性质上的相似性，以及能带拓扑理论广泛的适用性，启发笔者从能带拓扑的角度探讨边缘态的物理意义与性质.

本文利用解析与数值相结合的手段，计算体系的拓扑不变量，从而证明体系拓扑非平庸性，进而讨论体系的拓扑相变点与相变前后体系的拓扑性质，最后利用输运理论解释实验上观测到的体系边缘态局域位置的变化.

1 实验背景

实验中采用的弦球链系统如图1所示[4]，在光学导轨的一端用固定架F将弦的一头夹紧，弦的另一头跨过位于光学导轨另一端的定滑轮后，由砝码加一固定张力T.张紧的弦与导轨保持平行，其上等间距地固定有质量为mb的小球，小球间距为a.S1和S2是两个可以在导轨上滑动的滑块，记S1到第一个小球的距离为τ，S2到最后一个小球的距离为a-τ，可以通过挪动滑块的位置调节τ的大小.当用压块将弦紧压在S1和S2的刀口上时，刀口处弦的振幅被限制为零，但弦中张力并不会改变.

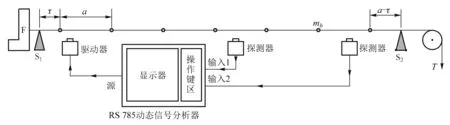
图1 弦球链系统振动模研究实验装置示意图

实验中所用的钢弦的线密度μ0=0.549 g/m，小球质量mb=0.127 g，两小球的间距为a=200 mm，弦张力T=9.01 N.

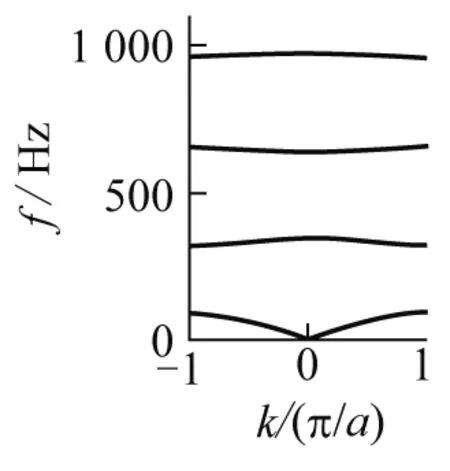
实验中采用PASCO公司的利用WA-9613驱动器和探测器来激励和探测弦链的振动，利用SR785动态信号分析器的正弦扫频工作模式来获取弦链系统的本征频谱.实验过程中可以改变弦链体系包含的总周期数N与S1到小球的距离τ，测得周期弦链系统在不同参数条件下的频谱图，测量结果如图2所示.

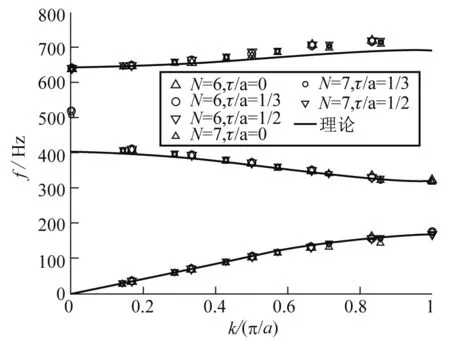
图2 弦球链系统频谱图

从图2中可以看出，体系的能谱存在带状结构，同时，在每一个能隙之间或能隙的边缘(k=0，π/a处)存在一个边缘态能量.数值计算与实验测量的数据表明，随着刀口S1位置的变化，即τ值的改变，边缘态的能量会在能隙之间移动.在特殊参数条件下，边缘态的能量会处在带顶或带底的位置，即能隙的边缘处.但在这整个过程中，边缘态始终存在.表1展示了在N=6的条件下，第二级带隙中的边缘态能量对应的共振频率随τ变化的理论值与实验值.

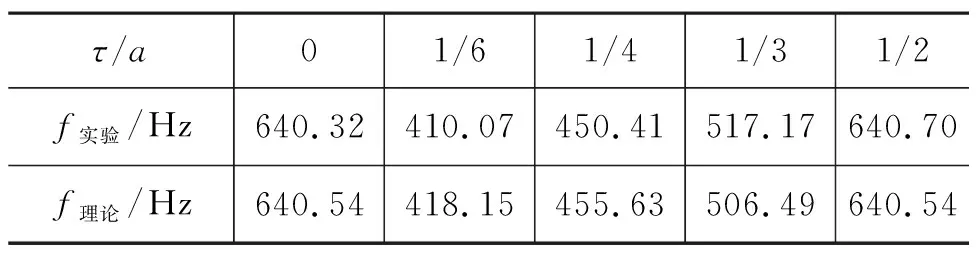
表1 N=6第二带隙态频率与τ/a的关系

同时，可以解析求解边缘态波函数在不同τ值下的函数形式，其具有e-i(k1+ik2)x的普适形式.因此，k2为正值时，代表体系局域在右边缘，反之代表体系局域在左边缘.在图3中画出了第1级带隙中k2随τ的变化，可以看到τ的变化会改变k2的正负，由此改变体系边缘态波函数的局域位置，对其他级的能隙亦是如此.

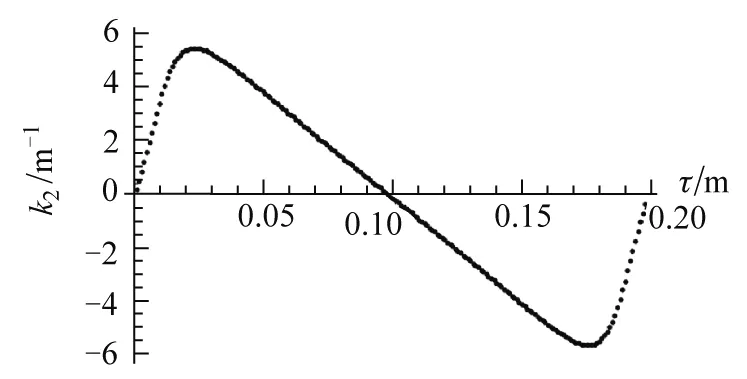
图3 第一级带隙中k2关于τ的变化曲线

规定波函数局域位置从左端变到右端再回到左端为一次来回，数值计算不同级带隙中边缘态波函数在τ从0增加到a时的来回次数nt，结果如表2所示.笔者发现，nt恰好等于边缘态所处能隙的级次(即ntj=j).

表2 来回次数nt与所处能隙级次的关系

为了更深入地解释上述实验与数值模拟的结果，本文利用能带拓扑的语言来处理这个体系.

2 拓扑不变量的计算

为了在弦球链体系上定义并计算拓扑不变量，先从体系的动力学方程出发，设体系的本征频率为ω，同时以刀口S1处为坐标原点，有

(1)

这是一个广义本征值问题，其中

(2)

弦球链体系具有x方向上的周期性，根据Bloch定理，波函数y(x)可以表示为Bloch解ψk(x)=eikxuk(x)的形式.

2.1 一维情况

弦球链体系在实验上是一个一维体系，故本文从一维情况下的拓扑分类理论[5]出发，来讨论体系可能具有的拓扑不变量.

体系的Bloch解所满足的方程为

(3)

从式(3)可以看出，体系在时间反演操作(x→x，i→-i，k→-k)下保持不变.同时，体系是无自旋的连续体系，故不存在粒子-空穴对称性与手征对称性.利用Altland-Zirnbauer分类法[5]，弦球链体系应当从属于AI类，而AI类在一维情况下没有非平庸的拓扑不变量.因此，在一维情况下讨论，弦球链体系是一个拓扑平庸的体系.

2.2 准二维情况

而弦球链体系还可以做准二维等价，从准二维等价出发，同样利用拓扑分类理论，体系就具有非平庸的拓扑不变量，从而可以从能带拓扑的角度解释实验上观测到的现象.

由式(1)、(2)可知，波函数y(x)是关于τ的函数，可记为ψk，τ(x)=eikxuk，τ(x)，同时，实验设置保证了τ也是体系的一个周期性参量，即当τ改变一个周期长度a时，体系复原，这与波矢在改变一个布里渊区之后复原的性质相同.因此通过将τ视为另一个维度的准波矢，可以将弦球链体系中的周期性参量(k，τ)映射为二维体系中的(kx，ky).上述准二维等价的做法也被应用在探究一维光子晶体[6]与一维准晶[7]的拓扑性质中.

准二维体系中的Bloch解也满足式(3)，但区别在于，由于τ被映射为准二维体系的波矢，在做时间反演变换时，对应的变换应当为：x→x，i→-i，k→-k，τ→-τ.式(3)在上述变换下，不再具有时间反演对称性.同样利用Altland-Zirnbauer分类法[5]，准二维等价下的弦球链体系应当从属于A类，而A类在二维情况下对应的拓扑不变量即为陈数.

在弦球链体系中，第n条能带的Berry曲率Ωn与陈数Cn的具体定义如下[8]：

Ωn=i[∇k×]

(4)

其中|ψn，k(r)>=eikx|un，k(r)>为第n条能带的Bloch波函数，且 (k，τ)映射为k=(kx，ky).

值得注意的是，式(4)是建立在周期性边界条件上的，而真实的体系是开边界条件.而Bulk-edge correspondence[9]使得周期性边界条件下定义并计算的拓扑不变量能够给出开边界条件下的边缘态的物理性质(例如电导).

利用解析与数值相结合的方式，求解了第1—4条能带的陈数，结果如图4所示.可以看出，每一条能带的陈数均为-1，因此准二维体系的能带是拓扑非平庸的，实验上观测到的带隙态在准二维拓扑的意义下，是拓扑保护的边缘态.

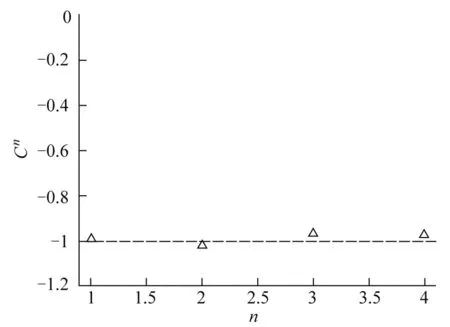
图4 第1-4条能带的陈数

3 拓扑相与拓扑相变

陈数作为一个拓扑不变量，不会随着参数的连续微小变化而发生改变.因此，连续的变化实验体系的其他参数，应当不改变体系的拓扑非平庸性.然而，当参数变化到引起体系的能隙闭合时，绝热定理失效[10]，陈数不再是良定义的拓扑不变量，此时继续变化参数让能隙重新打开后，体系的拓扑不变量就有可能发生变化，由此导致拓扑性质的变化.这样的变化过程称为拓扑相变，能隙闭合的参数点称为拓扑相变点.

选取小球质量mb为体系的可变参量，来探讨体系可能发生的拓扑相变.首先，利用数值方法求解出不同mb下的能谱，结果如图5所示.可以看出mb=0时能隙闭合，是体系的相变点.

mb=0.5 g

在3中已经验证了mb=0.127 g的时候，体系处于拓扑非平庸项，每条能带的陈数为-1.因此，利用拓扑不变量的性质，所有正小球质量的体系，其每条能带的陈数应与mb=0.127 g的情况相同.为此本文做了数值上的验证，结果见图6.

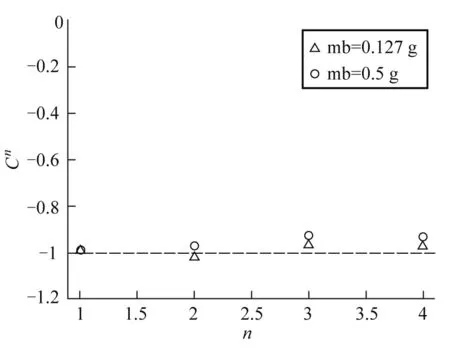
图6 正质量区域第1—4条能带的陈数

可以看出数值的结果与理论上的预测是相吻合的，在实验的意义上，更换不同的小球质量，都应当能测量到边缘态的存在，本文在4中会说明，这些边缘态都有同样的准二维输运性质.

在相变点mb=0，同样计算了对应的陈数，得到的结果为0，说明体系是一个拓扑平庸态，不再有拓扑保护的边缘态出现，这与笔者的物理直觉是吻合的.

在经过相变点之后的负质量区域，利用同样的方法计算陈数，结果如图7所示.

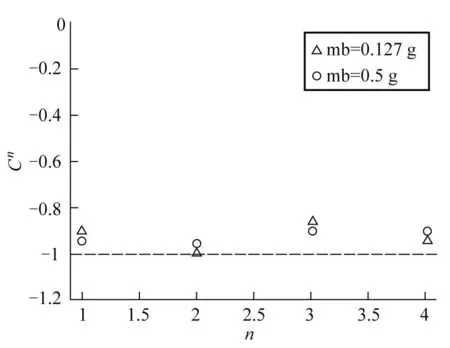
图7 负质量区域第1—4条能带的陈数

可以看出，在经过相变点到达负质量区域之后，体系仍然是一个拓扑非平庸项.也就是说，如果可以实现一种“缺陷”型的弦链体系，一样可以探测到拓扑保护的边缘态的存在.基于上述的讨论，可以给出体系的相图.

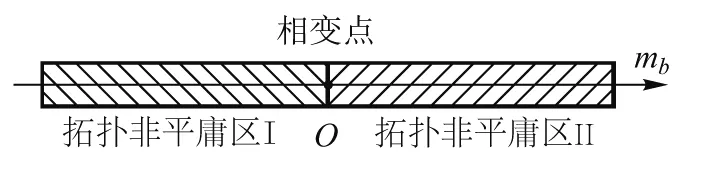
图8 弦球链体系相图(以mb为参数)

4 输运性质

在本小节中，将利用准二维的输运理论来解释边缘态局域位置随τ的变动.

准二维弦球链体系满足的方程为

(5)

由于cos势与δ函数势的同伦等价性，可以将弦球链体系类比二维整数量子霍尔效应体系在紧束缚模型下的一维等效方程[11]：

(6)

在整数量子霍尔效应中，外场对体系的驱动可以等效为相位ky-2mφ进行一个周期的平移，对应到弦球链体系中，即τ变化一个周期长度.该过程对应的电导可利用Kubo公式[8]进行计算，即

(7)

其中σn为第n条能带贡献的电导，因此，当体系的能量处在第j级带隙中时，总电导为

(8)

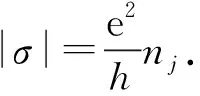
(9)

利用2中陈数的计算结果，nj=j.

准二维空间的输运体现在一维的实验体系中，就对应边缘态局域位置的变化，因此当τ改变一个周期时，第j级的边缘态局域位置的来回次数ntj=nj=j.这与1中基于求解波函数方法得到的来回次数的结果是一致的.因此边缘态局域位置的变化，可以利用准二维体系的输运理论来解释.

5 总结与展望

本文将能带拓扑的理论拓展到了弦球链体系中，先通过拓扑分类理论确定了一维与准二维情况下体系对应的拓扑不变量，而后计算得到了准二维体系不同能带的陈数，由此论证了边缘态的拓扑保护性质.并以小球的质量为参数，讨论了体系的拓扑相变点，用数值的方法确定了相变点前后的拓扑相，得到了体系的相图.值得说明的是，虽然负质量区域是“非物理”的，但这一部分的讨论使得本文的结果在理论上更具完整性.最后通过准二维输运理论定量解释了边缘态局域位置的变化，而该现象利用经典方法无法给出直观且定量的解释.

同时，在研究过程中，仍遇到了一些尚未解决的问题，例如，体系的动力学方程对应的是一个广义本征值问题，无法从中提取等效的哈密顿量.

能带拓扑理论的阐释赋予了弦球链体系更深刻的物理内涵，揭示了看似简单的经典体系其实蕴含着非平庸的能带拓扑.基于能带拓扑理论，还可以讨论更多的体系，例如杂质掺杂的弦球链体系、非整数周期的弦球链体系，这些都有待进一步的研究.

致谢：在本工作的研究过程中，得到了北京大学物理学院荀坤老师、吴宜家学长的支持和帮助，在此特致谢意！