矩形薄膜受迫横振动问题的求解及可视化

周纪晨，郭 琴

(江西师范大学 物理与通信电子学院，江西 南昌 330022 )

均匀薄膜的微小横振动是典型的波动方程问题，随着科学技术的发展，膜振动理论被应用于膜乐器的发声仿真[1]、人体耳膜振动的病理研究[2]以及植物细胞膜振动的超声育种[3]等．并且，由于工程结构的轻型化，薄膜结构在建筑、机械电子、航空航天等领域中也有着广泛的用途，因此薄膜振动的研究具有重要的意义．各类相关问题的讨论也十分丰富，如林文静等人分析了圆形膜和扇形膜自由振动问题[4]，罗吉等人研究了圆环膜自由振动模型[5]，章礼华等人构造了等腰直角三角形膜振动解析解[6]，以上有界薄膜的自由振动问题通常采用分离变量法[4-6]．对于更为复杂的薄膜受迫振动问题[7]，直接应用分离变量法求解二阶非齐次线性方程，需要用到非齐次线性方程解的定理，求解过程比较繁琐．采用冲量定理法结合傅里叶级数法能使问题的求解更加简洁.本文的研究有助于加强学生对受迫振动问题的冲量定理解法的掌握，经文献调研本文的研究内容未见发表．数值模拟是进一步探究膜振动规律的有效途径[8,9]，因此本文对示例结果进行作图分析，进一步验证结果的合理性，完整体现了矩形膜振动形态及其特点．

1 四周固定的矩形膜振动的定解问题

utt-c2Δ2u=0

(1)

图1 二维薄膜受力与坐标系建立

若膜上有横向外力作用，记单位面积上横向外力为F(x,y,t)，则单位质量上的横向外力f(x,y,t)=F(x,y,t)/ρ，薄膜受迫振动方程为

utt-c2Δ2u=f(x,y,t)

(2)

若膜四周边界固定(0≤x≤a,0≤y≤b)，则边界条件为

u(x,y,t)|x=0=u(x,y,t)|x=a=0

(3)

u(x,y,t)|y=0=u(x,y,t)|y=b=0

(4)

假设初始时刻膜上有初始位移φ(x,y)和初始速度ψ(x,y)．综上所述，本文研究的定解问题(t≥0)为

(5)

利用叠加原理，可将以上问题拆成两个定解问题，令u(x,y,t)=uⅠ(x,y,t)+uⅡ(x,y,t)，其中uⅠ满足非零初始条件下齐次方程问题(可采用傅里叶级数法求解)，uⅡ满足零值初始条件下非齐次方程问题(可运用冲量定理法求解)．

(6)

(7)

为便于分析，借助如下例题详细说明本文解法．

2 具有初始条件的矩形膜受迫振动问题解法示例

均匀各向同性弹性薄膜，宽为a，长为b，四周夹紧，初始位移为Axy(a-x)(b-y)，初始速度为0，单位面积所受的横向外力为ρf(x,y,t)=ρxysinωt，求解此矩形膜的横振动．

分析：由题意此问题适合采用薄膜受迫振动方程进行求解，边界条件同式(3)、式(4)，该定解问题可表达为

(8)

以上定解问题可拆成非零值初始条件下的齐次方程问题和零值初始条件下的非齐次方程问题.

2.1 具有初始条件的矩形膜自由振动下的解析解

接下来采用傅里叶级数法求解以下问题:

(9)

根据傅里叶级数法，由第一类齐次边界条件可设其试探解为

(10)

将式(10)代入式(9)中的泛定方程，得

(11)

解得

Tmn(t)=Amncosωmnt+Bmnsinωmnt

(12)

其中，薄膜本征振动的圆频率为

(13)

故得

(14)

再代入初始条件得

Axy(a-x)(b-y)

(15)

(16)

由式(15)，可利用傅里叶系数公式求解Amn：

(17)

由式(16)，利用比较系数法易得

Bmn=0

(18)

故式(9)的解为

(19)

2.2 零值初始条件矩形膜受迫振动下的解析解

下面采用冲量定理法求解以下问题:

(20)

问题式(20)表示矩形膜在受到单位质量的横向外力作用下作振动．运用冲量定理法的物理思想是，把持续作用引起的振动，看作单位质量薄膜所受“瞬时力”引起的振动的叠加；而作用在(τ,τ+dτ)时间段上的“瞬时力”的冲量可以转化为在τ+dτ时刻薄膜的初速度．故可转为求解关于v(x,y,t;τ)在初始速度作用下的自由振动问题：

(21)

参照边界条件，设其试探解为

(22)

将式(22)代入式(21)中的泛定方程，分离出Tmn的常微分方程并求解得

(23)

其中圆频率ωmn同式(13)，代入初始条件

(24)

vt(x,y,τ)=

(25)

比较两边系数得

Amn(τ)=0

(26)

利用傅里叶系数公式得

(27)

至此，已求得式(22)的完整表达式:

(28)

因此式(20)的解为

(29)

综上，已求得定解问题(8)的解析解:

u(x,y,t)=uⅠ(x,y,t)+uⅡ(x,y,t)=

(30)

3 理论解的讨论和可视化分析

下面对式(30)进行作图分析，展现四周固定矩形膜受迫振动的物理图像．

3.1 受迫矩形膜的振动特点

为探究周期性横向外力F=ρxysinωt的圆频率ω对膜上各点振动的影响，我们对式(29)作如下变换:

(31)

当外力的圆频率ω等于固有圆频率ωmn时(ω=ωmn):

(32)

其中第一项振幅为t/2，随着t增大而无限增大，直至达到薄膜振动承受极限，最终膜破裂，因此这对于研究共振在生产实际中带来的影响具有一定的指导意义．

为验证以上理论分析的合理性，考察长宽分别为b=2π,a=π的矩形膜，取膜上点x=π/2,y=π，作其振动位移随时间变化的图像即u(x,y,t)-t图，如图2、图3所示．其中式(29)中系数c=1．通过大量作图(这里只呈现两幅图)得出结论：当驱动力圆频率与固有圆频率相等时，薄膜将产生位移共振[11](如图2)；当两者十分接近但不相等时，薄膜将出现“拍”的现象(如图3)．

图2 位移共振现象

图3 “拍”现象

3.2 受迫矩形膜共振下的振动形态

为进一步了解矩形膜的整体振动形态变化，设式(30)中系数A=1,c=1，作出不同共振圆频率下u(x,y,t)的三维图像，来观察矩形膜(b=2π,a=π)随位移共振圆频率变化的三维动态图像．

图4是同一时刻不同共振圆频率的振动图像．可以得出结论：在同一时刻下，共振圆频率越大，矩形膜的表面褶皱越多，因为外界影响过快导致膜的变化也更为显著．

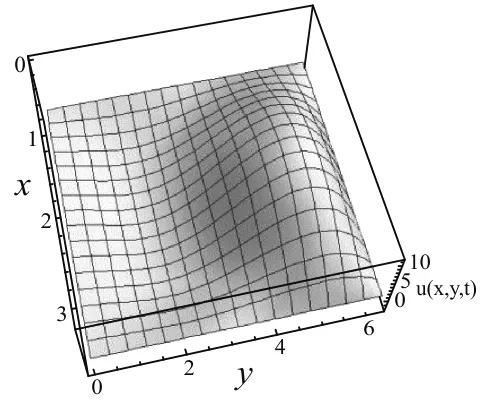
w(1,1)=1.118 03

图5是不同时刻同一共振圆频率的振动图像．可得出结论：在不同时刻下，由于外界驱动力以及初始位移的存在，矩形膜将呈现出不同于本征振动的一系列振动形态．

t=1.4

4 结论

本文将一维受迫弦振动定解问题的解法有效推广至二维矩形膜振动问题，充分运用冲量定理法中的物理思想，得到了四周固定的均匀矩形薄膜在受迫振动下的解析解．通过求解典型例题，使此类推广解法的使用更加清晰易懂．同时，对受迫振动的理论解进行了作图分析，使其蕴含的物理意义更加具体形象，振动特点更为直观．希望本文的研究可以加深学生对二维矩形膜振动问题的理解以及加强对数学物理方法相关理论的掌握． 二维矩形膜非齐次振动问题的冲量定理解法还可推广到二维有源(汇)输运问题中去．